บ้าน

กระจกด้านหน้า

ฟังก์ชันที่มีขนาดใหญ่เป็นอนันต์มีคุณสมบัติของมัน นิยามของฟังก์ชันที่มีขนาดใหญ่เป็นอนันต์ ฟังก์ชันที่ไม่มีที่สิ้นสุด

ฟังก์ชันที่มีขนาดใหญ่เป็นอนันต์มีคุณสมบัติของมัน นิยามของฟังก์ชันที่มีขนาดใหญ่เป็นอนันต์ ฟังก์ชันที่ไม่มีที่สิ้นสุด

ให้คำจำกัดความของลำดับที่ใหญ่เป็นอนันต์ แนวคิดเรื่องย่านใกล้เคียงของจุดที่อนันต์ได้รับการพิจารณา ให้คำจำกัดความสากลของขีดจำกัดของลำดับ ซึ่งใช้กับทั้งขีดจำกัดจำกัดและไม่จำกัด มีการพิจารณาตัวอย่างการประยุกต์ใช้คำจำกัดความของลำดับที่มีขนาดใหญ่เป็นอนันต์

เนื้อหา

ดูเพิ่มเติมที่: การกำหนดขีดจำกัดของลำดับ

คำนิยาม

ลำดับต่อมา (βn) เรียกว่าเป็นลำดับที่ใหญ่เป็นอนันต์ถ้าสำหรับเลข M ใดๆ ไม่ว่าจะมากขนาดไหนก็ตาม มันก็มีอยู่เช่นนั้น จำนวนธรรมชาติ N M ขึ้นอยู่กับ M โดยที่สำหรับ n ธรรมชาติทั้งหมด > N M จะมีความไม่เท่าเทียมกันดังต่อไปนี้:
|β n | >ม.
ในกรณีนี้พวกเขาเขียน
.
หรือที่.
พวกเขาบอกว่ามันมีแนวโน้มที่จะไม่มีที่สิ้นสุดหรือ บรรจบกันสู่อนันต์.

ถ้าเริ่มจากเลข N บางตัว 0 , ที่
( มาบรรจบกันที่บวกอนันต์).
ถ้าอย่างนั้น
( มาบรรจบกันที่ลบอนันต์).

ให้เราเขียนคำจำกัดความเหล่านี้โดยใช้สัญลักษณ์เชิงตรรกะของการดำรงอยู่และความเป็นสากล:
(1) .
(2) .
(3) .

ลำดับที่มีขีดจำกัด (2) และ (3) เป็นกรณีพิเศษของลำดับที่มีขนาดใหญ่อย่างไม่สิ้นสุด (1) จากคำจำกัดความเหล่านี้ ถ้าขีดจำกัดของลำดับเท่ากับบวกหรือลบอนันต์ ก็จะเท่ากับอนันต์ด้วย:
.
แน่นอนว่าสิ่งที่ตรงกันข้ามไม่เป็นความจริง สมาชิกของลำดับอาจมีเครื่องหมายสลับกัน ในกรณีนี้ ขีดจำกัดอาจเท่ากับอนันต์ แต่ไม่มีเครื่องหมายเฉพาะเจาะจง

โปรดทราบด้วยว่าหากคุณสมบัติบางอย่างเก็บไว้สำหรับลำดับใดลำดับหนึ่งซึ่งมีขีดจำกัดเท่ากับอนันต์ ดังนั้นคุณสมบัติเดียวกันนั้นจะคงไว้สำหรับลำดับซึ่งมีขีดจำกัดเท่ากับบวกหรือลบอนันต์

ในตำราแคลคูลัสหลายเล่ม คำจำกัดความของลำดับขนาดใหญ่อย่างไม่สิ้นสุดระบุว่าเลข M เป็นบวก: M > 0 - อย่างไรก็ตามข้อกำหนดนี้ไม่จำเป็น ถ้ายกเลิกก็ไม่มีความขัดแย้งเกิดขึ้น เป็นเพียงค่าเล็กน้อยหรือค่าลบที่ไม่น่าสนใจสำหรับเรา เรามีความสนใจในพฤติกรรมของลำดับสำหรับค่าบวกขนาดใหญ่โดยพลการของ M

ดังนั้น หากจำเป็น M อาจถูกจำกัดจากด้านล่างด้วยจำนวน a ใดๆ ที่กำหนดไว้ล่วงหน้า กล่าวคือ เราสามารถสรุปได้ว่า M > a > 0 เมื่อเรากำหนด ε - พื้นที่ใกล้เคียงของจุดสิ้นสุด ดังนั้นข้อกำหนด ε

เป็นสิ่งสำคัญ สำหรับค่าลบ ไม่สามารถชดเชยความไม่เท่าเทียมกันได้เลย

ย่านของจุดที่อนันต์

เมื่อเราพิจารณาขีดจำกัดอันจำกัด เราได้แนะนำแนวคิดเรื่องย่านใกล้เคียงของจุดหนึ่ง จำได้ว่าบริเวณใกล้เคียงของจุดสิ้นสุดเป็นช่วงเปิดที่มีจุดนี้ เรายังแนะนำแนวคิดเรื่องย่านใกล้เคียงของจุดที่อนันต์ได้ด้วย
ให้ M เป็นจำนวนใดก็ได้ย่านของจุด “อินฟินิตี้”
, , เรียกว่าเซตย่านของจุด “อินฟินิตี้”
ย่านจุด “บวกอินฟินิตี้”ย่านของจุด “อินฟินิตี้”

ในบริเวณใกล้กับจุด “ลบอนันต์”
(4) ,
พูดอย่างเคร่งครัด พื้นที่ใกล้เคียงของจุด "อนันต์" คือฉาก 1 ที่ไหน ม 2 และม

- จำนวนบวกตามอำเภอใจ เราจะใช้คำจำกัดความแรกเนื่องจากง่ายกว่า แม้ว่าทุกสิ่งที่กล่าวด้านล่างนี้จะเป็นจริงเมื่อใช้คำจำกัดความ (4)

ตอนนี้เราสามารถให้คำจำกัดความแบบรวมของขีดจำกัดของลำดับที่ใช้กับทั้งขีดจำกัดจำกัดและไม่จำกัด.
คำจำกัดความสากลของขีดจำกัดลำดับ

จุด a (จำกัดหรือที่อนันต์) คือขีดจำกัดของลำดับ ถ้าย่านใกล้เคียงใดๆ ของจุดนี้ มีจำนวนธรรมชาติ N โดยที่องค์ประกอบทั้งหมดของลำดับที่มีตัวเลขเป็นของย่านนี้

ดังนั้น หากมีขีดจำกัด ภายนอกย่านใกล้เคียงของจุด a จะมีสมาชิกของลำดับได้เพียงจำนวนจำกัดหรือเซตว่างเท่านั้น เงื่อนไขนี้จำเป็นและเพียงพอ การพิสูจน์คุณสมบัตินี้เหมือนกับการพิสูจน์ขีดจำกัดอันจำกัดทุกประการ
คุณสมบัติของบริเวณใกล้เคียงของลำดับมาบรรจบกัน
เพื่อให้จุด a (จำกัดหรือที่อนันต์) เป็นจุดจำกัดของลำดับ มีความจำเป็นและเพียงพอที่นอกย่านใกล้เคียงใดๆ ของจุดนี้ จะมีเงื่อนไขจำนวนจำกัดของลำดับหรือเซตว่าง

การพิสูจน์ .
บางครั้งก็มีการแนะนำแนวคิดของ ε - ย่านใกล้เคียงของจุดที่ไม่มีที่สิ้นสุด
จำได้ว่า ε-บริเวณใกล้เคียงของจุดจำกัด a คือเซต มาแนะนำกันดีกว่า- ให้ ε แทนพื้นที่ใกล้เคียงของจุด a
.
แล้วถึงจุดสิ้นสุด
;
;
.
สำหรับจุดที่ไม่มีที่สิ้นสุด:

การใช้แนวคิดของ ε-ย่านใกล้เคียง เราสามารถให้คำจำกัดความสากลอีกประการหนึ่งของขีดจำกัดของลำดับได้: จุด a (เทอร์มินัลหรือที่อนันต์) คือขีดจำกัดของลำดับหากมี ε > 0 จำนวนบวก
.

มีจำนวนธรรมชาติ N ε ขึ้นอยู่กับ ε ซึ่งสำหรับตัวเลขทั้งหมด n > N ε เงื่อนไข x n อยู่ใน ε-บริเวณใกล้เคียงของจุด a:
.

การใช้สัญลักษณ์เชิงตรรกะของการดำรงอยู่และความเป็นสากล คำจำกัดความนี้สามารถเขียนได้ดังนี้:

ตัวอย่างของลำดับที่มีขนาดใหญ่อนันต์

.
ตัวอย่างที่ 1
(1) .
ให้เราเขียนคำจำกัดความของลำดับที่ใหญ่เป็นอนันต์:
.

ในกรณีของเรา
.
เราแนะนำตัวเลข และ เชื่อมโยงพวกมันกับอสมการ:
.
ตามคุณสมบัติของอสมการ ถ้า และ แล้ว
โปรดทราบว่าอสมการนี้มีไว้สำหรับ n ใดๆ
ดังนั้นคุณสามารถเลือกได้ดังนี้:

ที่ ;
.
ที่ .

ดังนั้น สำหรับใครก็ตาม เราสามารถหาจำนวนธรรมชาติที่ตรงกับอสมการได้

แล้วสำหรับทุกคน
.

(2) .
ซึ่งหมายความว่า.
.

นั่นคือลำดับมีขนาดใหญ่อย่างไม่สิ้นสุด
.
.

ตัวอย่างที่ 2
.
ใช้นิยามของลำดับที่ใหญ่เป็นอนันต์แสดงว่า

คำศัพท์ทั่วไปของลำดับที่กำหนดมีรูปแบบ:

แล้วสำหรับทุกคน
.

ป้อนตัวเลขและ:
(3) .
ซึ่งหมายความว่า.
.

นั่นคือลำดับมีขนาดใหญ่อย่างไม่สิ้นสุด
.
จากนั้นสำหรับทุกคนสามารถหาจำนวนธรรมชาติที่ตรงกับอสมการได้ ดังนั้นสำหรับทุกคน
.

ซึ่งหมายความว่า.
.

ตัวอย่างที่ 3
.

ให้เราเขียนคำจำกัดความของขีดจำกัดของลำดับเท่ากับลบอนันต์:

แล้วสำหรับทุกคน
.

จากนี้จะเห็นชัดเจนว่าถ้า และ แล้ว
.
เนื่องจากสำหรับสิ่งใดสิ่งหนึ่งจึงเป็นไปได้ที่จะหาจำนวนธรรมชาติที่ตรงกับอสมการได้
(2) .

ให้ไว้ เนื่องจาก N เราสามารถใช้จำนวนธรรมชาติใดๆ ที่เป็นไปตามอสมการต่อไปนี้: = 1, 2, 3, ... , ที่
;
;
.

ตัวอย่างที่ 4
.
จากนั้นสำหรับทุกคนสามารถหาจำนวนธรรมชาติที่ตรงกับอสมการได้ ดังนั้นสำหรับทุกคน
.

ให้เราเขียนคำศัพท์ทั่วไปของลำดับ:
.
ใช้นิยามของลำดับที่ใหญ่เป็นอนันต์แสดงว่า

ให้เราเขียนคำจำกัดความของขีดจำกัดของลำดับเท่ากับบวกอนันต์:
เนื่องจาก n เป็นจำนวนธรรมชาติ ดังนั้น n
เราแนะนำตัวเลขและ M ซึ่งเชื่อมโยงกับความไม่เท่าเทียมกัน:

ดังนั้น สำหรับจำนวน M ใดๆ เราสามารถหาจำนวนธรรมชาติที่ตรงกับอสมการได้

แล้วสำหรับทุกคน วรรณกรรมที่ใช้:แอล.ดี. คุดรยาฟต์เซฟ. หลักสูตรการวิเคราะห์ทางคณิตศาสตร์ เล่มที่ 1 มอสโก 2546 ซม. นิโคลสกี้. หลักสูตรการวิเคราะห์ทางคณิตศาสตร์ เล่มที่ 1 มอสโก 2526ดูเพิ่มเติมที่: การทำงาน y=ฉ(x) เรียกว่าไม่มีที่สิ้นสุด ที่ x →ก

หรือเมื่อใด

x →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุด=(เรียกว่าฟังก์ชั่นขนาดเล็ก เรียกว่าเป็นฟังก์ชันที่มีขีดจำกัด ณ จุดที่กำหนดเป็นศูนย์

ตัวอย่าง. →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุด 1. ฟังก์ชั่น เรียกว่าฉ(x) เรียกว่า→0.

3. →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุด-1) 2 มีค่าน้อยมากที่ เรียกว่า→1 เนื่องจาก (ดูรูป) เรียกว่า→0.

4. →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุด = 1/เรียกว่า 2. ฟังก์ชั่น เรียกว่า→∞.

ให้เราสร้างความสัมพันธ์ที่สำคัญดังต่อไปนี้:

ทฤษฎีบท.ถ้าฟังก์ชั่น วรรณกรรมที่ใช้:เป็นตัวแทนได้ด้วย การทำงานเป็นผลรวมของจำนวนคงที่ ขและขนาดอันไม่สิ้นสุด α(x): ฉ (x)=b+ α(x)ที่ .

ในทางกลับกัน ถ้า แล้ว ฉ (x)=ข+α(x), ที่ไหน ขวาน)ฉ(x) x →ก

การพิสูจน์.

1. ให้เราพิสูจน์ส่วนแรกของข้อความนี้ จากความเท่าเทียมกัน ฉ(x)=ข+α(x)ควร |ฉ(x) – ข|=| α|- แต่เนื่องจาก ขวาน)มีค่าน้อยมาก ดังนั้นสำหรับ ε โดยพลการ จะมี δ – ย่านใกล้เคียงของจุด ก,ต่อหน้าทุกคน เรียกว่าซึ่งคุณค่าต่างๆ ขวาน)ตอบสนองความสัมพันธ์ |α(x)|< ε. แล้ว |ฉ(x) – ข|< ε. และนี่ก็หมายความว่า

2. ถ้า แล้วสำหรับ ε ใด ๆ >0 สำหรับทุกคน เอ็กซ์จากบาง δ – ย่านใกล้เคียงของจุด กจะ |ฉ(x) – ข|< ε. แต่ถ้าเราแสดงว่า ฉ(x) – ข= α, ที่ |α(x)|< ε ซึ่งหมายความว่า ก– ไม่มีที่สิ้นสุด

ลองพิจารณาคุณสมบัติพื้นฐานของฟังก์ชันเล็กๆ กัน

ทฤษฎีบท 1ผลบวกเชิงพีชคณิตของ 2, 3 และโดยทั่วไปแล้ว จำนวนอนันต์ใดๆ ที่มีขอบเขตจำกัดถือเป็นฟังก์ชันอนันต์

การพิสูจน์- ให้เราพิสูจน์สองเทอม อนุญาต ฉ(x)=α(x)+β(x), ที่ไหน และ . เราต้องพิสูจน์ว่าสำหรับ ε เล็กๆ ใดๆ ก็ตาม > พบ 0 δ> 0 เช่นนั้นสำหรับ เรียกว่า, สนองความเหลื่อมล้ำ |x – ก|<δ , ถูกดำเนินการ |ฉ(x)|< ε.

งั้นมาแก้ไขตัวเลขตามใจชอบกันดีกว่า ε > 0. เนื่องจากตามเงื่อนไขของทฤษฎีบท α(x)เป็นฟังก์ชันเล็กๆ น้อยๆ แล้วก็มี δ 1 แบบนั้น > 0 ซึ่งก็คือ |x – ก|< δ 1 เรามี |α(x)|< ε / 2. ในทำนองเดียวกันเนื่องจาก เบต้า(x)มีค่าน้อยมาก แล้วก็จะมี δ 2 ดังกล่าว > 0 ซึ่งก็คือ |x – ก|< δ 2 เรามี - β(x)|< ε / 2.

เอาล่ะ δ=นาที(δ 1 , δ2 } .แล้วในบริเวณใกล้จุด กรัศมี δ ความไม่เท่าเทียมกันแต่ละอย่างก็จะเป็นที่พอใจ |α(x)|< ε / 2 และ - β(x)|< ε / 2. เพราะฉะนั้นในย่านนี้ก็จะมี

|ฉ(x)|=| α(x)+β(x)| ≤ |α(x)| - β(x)|< ε /2 + ε /2= ε,

เหล่านั้น. |ฉ(x)|< ε ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์

ทฤษฎีบท 2ผลคูณของฟังก์ชันอนันต์ ขวาน)สำหรับฟังก์ชันที่จำกัด →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดดูเพิ่มเติมที่: การทำงาน(หรือเมื่อ x→∞) เป็นฟังก์ชันที่เล็กที่สุด

การพิสูจน์- ตั้งแต่ฟังก์ชั่น →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดมีจำนวนจำกัดก็มีจำนวนจำกัด มเช่นนั้นสำหรับทุกค่า เรียกว่าจากบริเวณใกล้เคียงจุดหนึ่ง ก|ฉ(x)|≤Mนอกจากนี้ตั้งแต่นั้นเป็นต้นมา ขวาน)เป็นฟังก์ชันขั้นต่ำที่ การทำงานจากนั้นสำหรับ ε โดยพลการ > 0 มีพื้นที่ใกล้เคียงของจุด กซึ่งความไม่เท่าเทียมกันจะคงอยู่ |α(x)|< ε /ม- จากนั้นในย่านเล็กๆ เหล่านี้ เราก็มี - อัลฟ|< ε /ม= ε. และนี่หมายความว่า อัฟ– ไม่มีที่สิ้นสุด สำหรับโอกาสนี้ x→∞การพิสูจน์จะดำเนินการในทำนองเดียวกัน

จากทฤษฎีบทที่พิสูจน์แล้วมีดังนี้:

ข้อพิสูจน์ 1.ถ้าและแล้ว

ข้อพิสูจน์ 2.ถ้าและ ค= const แล้ว

ทฤษฎีบท 3อัตราส่วนของฟังก์ชันอนันต์ α(x)ต่อฟังก์ชัน →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดลิมิตที่แตกต่างจากศูนย์คือฟังก์ชันที่เล็กที่สุด

การพิสูจน์- อนุญาต . จากนั้น 1 /ฉ(x)มีฟังก์ชันจำกัด ดังนั้น เศษส่วนจึงเป็นผลคูณของฟังก์ชันน้อยและฟังก์ชันจำกัด เช่น ฟังก์ชันมีน้อยมาก

แคลคูลัสของขนาดจิ๋วและขนาดใหญ่

แคลคูลัสไม่สิ้นสุด- การคำนวณดำเนินการด้วยปริมาณที่น้อยมาก ซึ่งผลลัพธ์ที่ได้จะถือเป็นผลรวมอนันต์ของค่าที่น้อยที่สุด แคลคูลัสขั้นต่ำคือ แนวคิดทั่วไปสำหรับแคลคูลัสเชิงอนุพันธ์และอินทิกรัลซึ่งเป็นพื้นฐานของคณิตศาสตร์ระดับสูงสมัยใหม่ แนวคิดเรื่องปริมาณที่น้อยที่สุดมีความเกี่ยวข้องอย่างใกล้ชิดกับแนวคิดเรื่องขีดจำกัด

ไม่มีที่สิ้นสุด

ลำดับต่อมา ก nเรียกว่า ซม. นิโคลสกี้. หลักสูตรการวิเคราะห์ทางคณิตศาสตร์ เล่มที่ 1 มอสโก 2526, ถ้า . ตัวอย่างเช่น ลำดับของตัวเลขนั้นมีน้อยมาก

ฟังก์ชันนี้เรียกว่า เล็กน้อยในบริเวณใกล้เคียงจุดหนึ่ง เรียกว่า 0 ถ้า .

ฟังก์ชันนี้เรียกว่า ไม่มีที่สิ้นสุดที่อนันต์, ถ้า หรือ .

ฟังก์ชันที่น้อยที่สุดก็คือค่าความแตกต่างระหว่างฟังก์ชันกับลิมิตของมัน นั่นคือถ้า , ที่ ฉ(เรียกว่า) − ก = α( เรียกว่า) , .

ปริมาณมากอนันต์

ลำดับต่อมา ก nเรียกว่า ใหญ่อนันต์, ถ้า .

ฟังก์ชันนี้เรียกว่า ใหญ่เป็นอนันต์ใกล้กับจุดหนึ่ง เรียกว่า 0 ถ้า .

ฟังก์ชันนี้เรียกว่า ใหญ่เป็นอนันต์ที่อนันต์, ถ้า หรือ .

ในทุกกรณี อนันต์ทางด้านขวาของความเสมอภาคจะมีเครื่องหมายที่แน่นอน (ทั้ง "บวก" หรือ "ลบ") นั่นคือ ตัวอย่างเช่น ฟังก์ชัน เรียกว่าบาป เรียกว่ามีขนาดไม่ใหญ่เป็นอนันต์ที่

คุณสมบัติของขนาดอนันต์เล็กและใหญ่อนันต์

การเปรียบเทียบสิ่งเล็กๆ น้อยๆ

จะเปรียบเทียบปริมาณที่น้อยที่สุดได้อย่างไร?
อัตราส่วนของปริมาณที่น้อยที่สุดก่อให้เกิดสิ่งที่เรียกว่าความไม่แน่นอน

คำจำกัดความ

สมมติว่าเรามีค่าน้อยที่สุดα( เรียกว่า) และ β( เรียกว่า) (หรือลำดับที่ไม่สำคัญสำหรับคำจำกัดความ)

ในการคำนวณขีดจำกัดดังกล่าว จะสะดวกในการใช้กฎของโลปิตาล

ตัวอย่างการเปรียบเทียบ

โดยใช้ เกี่ยวกับ- Symbolism ผลลัพธ์ที่ได้สามารถเขียนได้ในรูปแบบต่อไปนี้ เรียกว่า 5 = โอ(เรียกว่า 3). ใน ในกรณีนี้บันทึกถูกต้อง 2เรียกว่า 2 + 6เรียกว่า = โอ(เรียกว่า) และ เรียกว่า = โอ(2เรียกว่า 2 + 6เรียกว่า).

ค่าที่เท่ากัน

คำนิยาม

ถ้า แล้วจึงเรียกปริมาณที่น้อยที่สุด α และ β เทียบเท่า ().
เห็นได้ชัดว่าปริมาณที่เท่ากันเป็นกรณีพิเศษของปริมาณที่น้อยที่สุดและมีลำดับเล็กน้อยเท่ากัน

เมื่อความสัมพันธ์สมมูลต่อไปนี้ถูกต้อง: , , .

ทฤษฎีบท

ขีดจำกัดของผลหาร (อัตราส่วน) ของปริมาณที่น้อยที่สุดสองปริมาณจะไม่เปลี่ยนแปลงหากหนึ่งในนั้น (หรือทั้งสองอย่าง) ถูกแทนที่ด้วยปริมาณที่เท่ากัน.

ทฤษฎีบทนี้มีความสำคัญในทางปฏิบัติเมื่อค้นหาขีดจำกัด (ดูตัวอย่าง)

ตัวอย่างการใช้งาน

กำลังเปลี่ยน สฉันn 2เรียกว่า ค่าเทียบเท่า 2 เรียกว่าเราได้รับ

ภาพสเก็ตช์ประวัติศาสตร์

แนวคิดเรื่อง "จิ๋ว" ได้รับการกล่าวถึงในสมัยโบราณเกี่ยวกับแนวคิดเรื่องอะตอมที่แบ่งแยกไม่ได้ แต่ไม่รวมอยู่ในคณิตศาสตร์คลาสสิก ได้รับการฟื้นคืนชีพอีกครั้งด้วยการถือกำเนิดของ "วิธีการแบ่งแยกไม่ได้" ในศตวรรษที่ 16 โดยแบ่งร่างที่กำลังศึกษาออกเป็นส่วนเล็ก ๆ

ในศตวรรษที่ 17 พีชคณิตของแคลคูลัสขนาดเล็กเกิดขึ้น เริ่มถูกกำหนดให้เป็นปริมาณตัวเลขที่น้อยกว่าปริมาณจำกัดใดๆ (ไม่เป็นศูนย์) แต่ยังไม่เท่ากับศูนย์ ศิลปะแห่งการวิเคราะห์ประกอบด้วยการร่างความสัมพันธ์ที่มีขนาดเล็กที่สุด (ดิฟเฟอเรนเชียล) จากนั้นจึงบูรณาการเข้าด้วยกัน

นักคณิตศาสตร์รุ่นเก่าได้นำแนวคิดนี้ไปทดสอบ ไม่มีที่สิ้นสุดการวิจารณ์ที่รุนแรง มิเชล โรลล์ เขียนว่าแคลคูลัสใหม่คือ “ ชุดของข้อผิดพลาดอันชาญฉลาด- วอลแตร์ตั้งข้อสังเกตอย่างเสียดสีว่าแคลคูลัสเป็นศิลปะในการคำนวณและวัดสิ่งต่าง ๆ ที่ไม่สามารถพิสูจน์ได้ว่ามีอยู่จริงอย่างแม่นยำ แม้แต่ Huygens ก็ยอมรับว่าเขาไม่เข้าใจความหมายของส่วนต่างของลำดับที่สูงกว่า

เป็นการเหน็บแนมแห่งโชคชะตา เราสามารถพิจารณาการเกิดขึ้นในช่วงกลางศตวรรษของการวิเคราะห์ที่ไม่ได้มาตรฐาน ซึ่งพิสูจน์ว่ามุมมองดั้งเดิม - สิ่งเล็กๆ น้อยๆ ที่เกิดขึ้นจริง - ก็มีความสอดคล้องกันและสามารถใช้เป็นพื้นฐานสำหรับการวิเคราะห์ได้

ดูเพิ่มเติม

มูลนิธิวิกิมีเดีย

2010.

ดูว่า "ใหญ่ไม่มีที่สิ้นสุด" ในพจนานุกรมอื่น ๆ คืออะไร: ปริมาณแปรผัน Y คือค่าผกผันของปริมาณน้อย X นั่นคือ Y = 1/X...

พจนานุกรมสารานุกรมขนาดใหญ่ ตัวแปร y คือค่าผกผันของค่า x ที่มีค่าน้อยที่สุด ซึ่งก็คือ y = 1/x * * * INFINITELY LARGE INFINITELY LARGE ปริมาณแปรผัน Y ผกผันกับปริมาณ X ที่น้อยที่สุด นั่นคือ Y = 1/X ...

พจนานุกรมสารานุกรม ในทางคณิตศาสตร์ ปริมาณแปรผันซึ่งในกระบวนการเปลี่ยนแปลงที่กำหนด จะกลายเป็นและคงอยู่ในค่าสัมบูรณ์มากกว่าจำนวนใดๆ ที่กำหนดไว้ล่วงหน้า การศึกษาบีบี สามารถลดปริมาณลงได้จนถึงการศึกษาขนาดจิ๋ว (ดู... ...

สารานุกรมผู้ยิ่งใหญ่แห่งสหภาพโซเวียต

แล้วสำหรับทุกคน วรรณกรรมที่ใช้:แอล.ดี. คุดรยาฟต์เซฟ. หลักสูตรการวิเคราะห์ทางคณิตศาสตร์ เล่มที่ 1 มอสโก 2546 ฟังก์ชั่นเล็กๆ น้อยๆ และคุณสมบัติพื้นฐานดูเพิ่มเติมที่: การทำงาน y=ฉ(x) เรียกว่าไม่มีที่สิ้นสุด

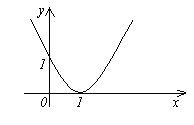
หรือเมื่อใด

ให้เราสร้างความสัมพันธ์ที่สำคัญดังต่อไปนี้:

ทฤษฎีบท.ถ้าฟังก์ชั่น วรรณกรรมที่ใช้:→∞ ถ้า หรือ เช่น ฟังก์ชันจิ๋วคือฟังก์ชันที่มีขีดจำกัด ณ จุดที่กำหนดเป็นศูนย์ การทำงานเป็นผลรวมของจำนวนคงที่ ขเป็นตัวแทนได้ด้วย α(x): ฉ (x)=b+ α(x)และขนาดอันไม่สิ้นสุด

ที่ . ฉ (x)=ข+α(x)ในทางกลับกัน ถ้า แล้ว ขวาน), ที่ไหน x →ก

การพิสูจน์.

– ไม่มีที่สิ้นสุดที่

ทฤษฎีบท 1ลองพิจารณาคุณสมบัติพื้นฐานของฟังก์ชันเล็กๆ กัน

การพิสูจน์ผลบวกเชิงพีชคณิตของ 2, 3 และโดยทั่วไปแล้ว จำนวนอนันต์ใดๆ ที่มีขอบเขตจำกัดถือเป็นฟังก์ชันอนันต์ ฉ(x)=α(x)+β(x)- ให้เราพิสูจน์สองเทอม อนุญาต > , ที่ไหน และ . เราต้องพิสูจน์ว่าสำหรับ ε เล็กๆ ใดๆ ก็ตาม δ> พบ 0 เรียกว่า 0 เช่นนั้นสำหรับ |x – ก|<δ , ถูกดำเนินการ |ฉ(x)|< ε.

, สนองความเหลื่อมล้ำ > 0. เนื่องจากตามเงื่อนไขของทฤษฎีบท α(x)งั้นมาแก้ไขตัวเลขตามใจชอบกันดีกว่า ε > เป็นฟังก์ชันเล็กๆ น้อยๆ แล้วก็มี δ 1 แบบนั้น |x – ก|< δ 1 เรามี |α(x)|< ε / 2. ในทำนองเดียวกันเนื่องจาก เบต้า(x) 0 ซึ่งก็คือ > เป็นฟังก์ชันเล็กๆ น้อยๆ แล้วก็มี δ 1 แบบนั้น |x – ก|< δ 2 เรามี - β(x)|< ε / 2.

เอาล่ะ δ=นาที(δ 1 , δ2 } .แล้วในบริเวณใกล้จุด กรัศมี δ มีค่าน้อยมาก แล้วก็จะมี δ 2 ดังกล่าว |α(x)|< ε / 2 และ - β(x)|< ε / 2. ความไม่เท่าเทียมกันแต่ละอย่างก็จะเป็นที่พอใจ

|ฉ(x)|=| α(x)+β(x)| ≤ |α(x)| - β(x)|< ε /2 + ε /2= ε,

เหล่านั้น. |ฉ(x)|< ε ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์

ทฤษฎีบท 2ผลคูณของฟังก์ชันอนันต์ ขวาน)สำหรับฟังก์ชันที่จำกัด →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดที่ การทำงาน(หรือเมื่อ x→∞) เป็นฟังก์ชันที่เล็กที่สุด

จากทฤษฎีบทที่พิสูจน์แล้วมีดังนี้:

ข้อพิสูจน์ 1.ถ้าและแล้ว

ข้อพิสูจน์ 2.ถ้าและ ค= const แล้ว

การพิสูจน์- อนุญาต - จากนั้น 1 /ฉ(x)มีฟังก์ชันจำกัด ดังนั้นเศษส่วน คือผลคูณของฟังก์ชันจิ๋วและฟังก์ชันมีขอบเขต เช่น ฟังก์ชันมีน้อยมาก

ความสัมพันธ์ระหว่างฟังก์ชันเล็กอนันต์และฟังก์ชันใหญ่อนันต์

ทฤษฎีบท 1ถ้าฟังก์ชั่น →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดมีขนาดใหญ่เป็นอนันต์ที่ การทำงานแล้วฟังก์ชัน 1 /ฉ(x)มีค่าน้อยมากที่ การทำงาน.

การพิสูจน์.ลองหาตัวเลขตามใจชอบกันเถอะ ε >0 และแสดงสิ่งนั้นให้กับบางคน δ>0 (ขึ้นอยู่กับε) สำหรับทุกคน เรียกว่าเพื่อที่ |x – ก|<δ ความไม่เท่าเทียมกันเป็นที่พอใจและนี่ก็หมายความว่า 1/ฉ(x)เป็นฟังก์ชันอนันต์ แท้จริงแล้วตั้งแต่นั้นเป็นต้นมา →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดเป็นฟังก์ชันที่มีขนาดใหญ่เป็นอนันต์ที่ การทำงานแล้วจะมี δ>0 เช่นนั้นทันที |x – ก|<δ ดังนั้น | ฉ(x)|> 1/ ε. แต่แล้วเพื่อสิ่งเดียวกัน เรียกว่า.

หรือเมื่อใด

ทฤษฎีบทสนทนาก็สามารถพิสูจน์ได้เช่นกัน

ทฤษฎีบท 2ถ้าฟังก์ชั่น →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุด- ไม่มีที่สิ้นสุดที่ การทำงาน(หรือ x→∞)และไม่หายไปแล้ว ย= 1/ฉ(x)เป็นฟังก์ชันที่มีขนาดใหญ่เป็นอนันต์

ดำเนินการพิสูจน์ทฤษฎีบทด้วยตัวเอง

หรือเมื่อใด

ดังนั้น คุณสมบัติที่ง่ายที่สุดของฟังก์ชันที่เล็กและใหญ่อย่างไม่สิ้นสุดสามารถเขียนได้โดยใช้ความสัมพันธ์แบบมีเงื่อนไขดังต่อไปนี้: ก≠ 0

ทฤษฎีบทจำกัด

ทฤษฎีบท 1ขีดจำกัดของผลรวมพีชคณิตของสอง สาม และโดยทั่วไปจำนวนฟังก์ชันที่แน่นอนจะเท่ากับผลรวมพีชคณิตของขีดจำกัดของฟังก์ชันเหล่านี้ เช่น

การพิสูจน์- ให้เราทำการพิสูจน์สองเทอมกัน เนื่องจากสามารถทำได้ในลักษณะเดียวกันไม่ว่าจะกี่เทอมก็ตาม อนุญาต .แล้ว ฉ(x)=ข+α(x)และ ก.(x)=ค+β(x)ในทางกลับกัน ถ้า แล้ว α และ β – ฟังก์ชั่นที่ไม่มีที่สิ้นสุด เพราะฉะนั้น,

ฉ(x) + ก(x)=(ข + ค) + (α(x) + β(x)).

เพราะ บี+ซีเป็นค่าคงที่และ α(x) + β(x)จึงเป็นฟังก์ชันอนันต์

ตัวอย่าง. -

ทฤษฎีบท 2ขีดจำกัดของผลคูณของสอง สาม และโดยทั่วไปจำนวนฟังก์ชันที่มีจำกัดจะเท่ากับผลคูณของขีดจำกัดของฟังก์ชันเหล่านี้:

การพิสูจน์- อนุญาต - เพราะฉะนั้น, ฉ(x)=ข+α(x)และ ก.(x)=ค+β(x)และ

fg = (b + α)(c + β) = bc + (bβ + cα + αβ)

งาน ก่อนคริสต์ศักราชมีค่าคงที่ การทำงาน bβ + c α + αβขึ้นอยู่กับคุณสมบัติของฟังก์ชันขั้นต่ำ จะมีปริมาณที่น้อยที่สุด นั่นเป็นเหตุผลว่าทำไม

ข้อพิสูจน์ 1.ตัวประกอบคงที่สามารถหาได้เกินเครื่องหมายจำกัด:

ข้อพิสูจน์ 2.ขีดจำกัดระดับ เท่ากับพลังขีดจำกัด:

ตัวอย่าง..

ทฤษฎีบท 3ขีดจำกัดของผลหารของสองฟังก์ชันจะเท่ากับผลหารของขีดจำกัดของฟังก์ชันเหล่านี้ ถ้าขีดจำกัดของตัวส่วนแตกต่างจากศูนย์ เช่น

การพิสูจน์- อนุญาต . เพราะฉะนั้น, ฉ(x)=ข+α(x)และ ก.(x)=ค+β(x), ที่ไหน α, β – ไม่มีที่สิ้นสุด ลองพิจารณาผลหาร

เศษส่วนเป็นฟังก์ชันที่เล็กที่สุดเพราะตัวเศษเป็นฟังก์ชันที่เล็กที่สุดและตัวส่วนมีขีดจำกัด ค 2 ≠0

หรือเมื่อใด

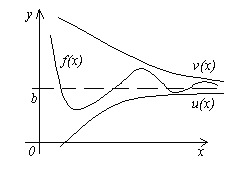
ทฤษฎีบท 4ให้สามฟังก์ชันได้รับ ฉ(x) คุณ(x)และ วี(เอ็กซ์)ตอบสนองความไม่เท่าเทียมกันคุณ (x)≤f(x)≤ วี(x)- ถ้าฟังก์ชั่น คุณ(x)และ วี(เอ็กซ์)มีขีดจำกัดเท่ากันที่ การทำงาน(หรือ x→∞) ตามด้วยฟังก์ชัน →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดมีแนวโน้มที่จะมีขีดจำกัดเท่ากัน กล่าวคือ ถ้า

, ที่ .

ความหมายของทฤษฎีบทนี้เห็นได้ชัดเจนจากรูป

ตัวอย่างการพิสูจน์ทฤษฎีบทที่ 4 มีอยู่ในตำราเรียน: Piskunov N. S. แคลคูลัสเชิงอนุพันธ์และอินทิกรัล เล่ม 1 - M.: Nauka, 1985

ทฤษฎีบท 5ถ้า ณ การทำงาน(หรือ x→∞) การทำงาน วรรณกรรมที่ใช้:ยอมรับค่าที่ไม่เป็นลบ y≥0และในขณะเดียวกันก็มีแนวโน้มที่จะถึงขีดจำกัด ขดังนั้นขีดจำกัดนี้จะต้องไม่เป็นค่าลบ: ข≥0.

การพิสูจน์- เราจะดำเนินการพิสูจน์โดยขัดแย้งกัน สมมุติว่า ข<0 , แล้ว |y – ข|≥|ข|ดังนั้นโมดูลัสส่วนต่างจึงไม่มีแนวโน้มจะเป็นศูนย์เมื่อใด การทำงาน- แต่แล้ว ยไม่ถึงขีดจำกัด ขดูเพิ่มเติมที่: การทำงานซึ่งขัดแย้งกับเงื่อนไขของทฤษฎีบท

ทฤษฎีบท 6ถ้าสองฟังก์ชัน →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดและ ก.(เอ็กซ์)สำหรับค่าทั้งหมดของอาร์กิวเมนต์ เรียกว่าตอบสนองความไม่เท่าเทียมกัน ฉ(x)≥ ก(x)และมีขีดจำกัด ความไม่เท่าเทียมกันก็จะยังคงอยู่ ข≥c.

การพิสูจน์.ตามเงื่อนไขของทฤษฎีบท ฉ(x)-ก(x) ≥0ดังนั้นตามทฤษฎีบทที่ 5 , หรือ .

ข้อจำกัดฝ่ายเดียว

จนถึงตอนนี้เราได้พิจารณากำหนดขีดจำกัดของฟังก์ชันเมื่อใด การทำงานในลักษณะตามอำเภอใจ เช่น ขีดจำกัดของฟังก์ชันไม่ได้ขึ้นอยู่กับว่ามันอยู่อย่างไร เรียกว่าเกี่ยวกับ กไปทางซ้ายหรือขวาของ ก- อย่างไรก็ตาม เป็นเรื่องปกติที่จะค้นหาฟังก์ชันที่ไม่มีขีดจำกัดภายใต้เงื่อนไขนี้ แต่ก็มีขีดจำกัดหาก การทำงานเหลืออยู่อีกด้านหนึ่งของ กซ้ายหรือขวา (ดูรูป) ดังนั้นจึงมีการแนะนำแนวคิดเรื่องขีดจำกัดด้านเดียว

ถ้า →∞ ถ้า หรือ เช่น ไม่มีที่สิ้นสุดมีแนวโน้มที่จะถึงขีด จำกัด ขดูเพิ่มเติมที่: เรียกว่าพุ่งไปเป็นจำนวนหนึ่ง กดังนั้น เรียกว่ายอมรับเฉพาะค่าที่น้อยกว่า กจากนั้นพวกเขาก็เขียนและโทร blimit ของฟังก์ชัน f(x) ที่จุด a ทางด้านซ้าย

แคลคูลัสของขนาดจิ๋วและขนาดใหญ่

แคลคูลัสไม่สิ้นสุด- การคำนวณดำเนินการด้วยปริมาณที่น้อยมาก ซึ่งผลลัพธ์ที่ได้จะถือเป็นผลรวมอนันต์ของค่าที่น้อยที่สุด แคลคูลัสของ infinitesimals เป็นแนวคิดทั่วไปสำหรับแคลคูลัสเชิงอนุพันธ์และอินทิกรัล ซึ่งเป็นพื้นฐานของคณิตศาสตร์ระดับสูงสมัยใหม่ แนวคิดเรื่องปริมาณที่น้อยที่สุดมีความเกี่ยวข้องอย่างใกล้ชิดกับแนวคิดเรื่องขีดจำกัด

ไม่มีที่สิ้นสุด

ฟังก์ชันนี้เรียกว่า เล็กน้อยในบริเวณใกล้เคียงจุดหนึ่ง เรียกว่า 0 ถ้า .

ฟังก์ชันนี้เรียกว่า ไม่มีที่สิ้นสุดที่อนันต์, ถ้า หรือ .

ปริมาณมากอนันต์

ในสูตรทั้งหมดด้านล่างนี้ ค่าอนันต์ทางด้านขวาของความเสมอภาคจะมีเครื่องหมายที่แน่นอน (อาจเป็น "บวก" หรือ "ลบ") นั่นคือ ตัวอย่างเช่น ฟังก์ชัน เรียกว่าบาป เรียกว่าไม่จำกัดทั้งสองด้าน มีขนาดไม่ใหญ่เป็นอนันต์ที่

ลำดับต่อมา ก nเรียกว่า ใหญ่อนันต์, ถ้า .

ฟังก์ชันนี้เรียกว่า ใหญ่เป็นอนันต์ใกล้กับจุดหนึ่ง เรียกว่า 0 ถ้า .

ฟังก์ชันนี้เรียกว่า ใหญ่เป็นอนันต์ที่อนันต์, ถ้า หรือ .

คุณสมบัติของขนาดอนันต์เล็กและใหญ่อนันต์

การเปรียบเทียบสิ่งเล็กๆ น้อยๆ

คำจำกัดความ

ในการคำนวณขีดจำกัดดังกล่าว จะสะดวกในการใช้กฎของโลปิตาล

ตัวอย่างการเปรียบเทียบ

โดยใช้ เกี่ยวกับ- Symbolism ผลลัพธ์ที่ได้สามารถเขียนได้ในรูปแบบต่อไปนี้ เรียกว่า 5 = โอ(เรียกว่า 3). ในกรณีนี้ รายการต่อไปนี้เป็นจริง: 2เรียกว่า 2 + 6เรียกว่า = โอ(เรียกว่า) และ เรียกว่า = โอ(2เรียกว่า 2 + 6เรียกว่า).

ค่าที่เท่ากัน

คำนิยาม

เมื่อความสัมพันธ์ที่เท่าเทียมกันต่อไปนี้ถูกต้อง (ซึ่งเป็นผลมาจากสิ่งที่เรียกว่าขีดจำกัดที่น่าทึ่ง):

ทฤษฎีบท

ทฤษฎีบทนี้มีความสำคัญในทางปฏิบัติเมื่อค้นหาขีดจำกัด (ดูตัวอย่าง)

ตัวอย่างการใช้งาน

กำลังเปลี่ยน สฉันn 2เรียกว่า ค่าเทียบเท่า 2 เรียกว่าเราได้รับ

ภาพสเก็ตช์ประวัติศาสตร์

ดูเพิ่มเติม

มูลนิธิวิกิมีเดีย

ดูว่า "ปริมาณน้อย" ในพจนานุกรมอื่น ๆ คืออะไร:

ปริมาณขนาดเล็กไม่สิ้นสุด- ปริมาณแปรผันในกระบวนการหนึ่ง หากในกระบวนการนี้ปริมาณเข้าใกล้ (มีแนวโน้ม) สู่ศูนย์อย่างไม่สิ้นสุด... สารานุกรมโพลีเทคนิคขนาดใหญ่

ไม่มีที่สิ้นสุด- ■ สิ่งที่ไม่รู้จัก แต่เกี่ยวข้องกับโฮมีโอพาธีย์... พจนานุกรมความจริงทั่วไป

ส่วนต่างๆ