Funções vetoriais do histórico de aparecimento de argumentos escalares. Especificando uma função usando um vetor verdade. Especificando usando uma árvore binária completa

e sua diferenciação.

Uma das maneiras mais simples de especificar uma curva espacial é especificar uma equação vetorial:

Onde é o vetor raio do ponto da curva, e - parâmetro que determina a posição do ponto.

Que. vetor variável existe uma função escalar . Na análise matemática, tais funções são chamadas de funções vetoriais de um argumento escalar.

Decompondo usando vetores unitários, a equação (1) pode ter a forma:

Esta expansão permite passar à equação paramétrica da curva:

Em outras palavras, especificar uma função vetorial é equivalente a especificar três funções escalares.

Em relação à função vetorial (1) que define esta curva, a própria curva é chamada de hodógrafo desta função. A origem das coordenadas é chamada neste caso de pólo do hodógrafo.

Deixe agora
E
- pontos da curva definidos pela equação (1). Além disso
, Um
Os vetores de raio desses pontos serão

E
.

Vetor
chamado de incremento de uma função vetorial
, correspondente ao incremento
seu argumento, e é denotado por
,

Função vetorial
será uma função contínua , Se

.

Para encontrar a derivada de
vamos proceder da seguinte forma -

.

Vamos agora definir a direção
. É óbvio que colinear com
e em
direcionado na mesma direção que
e quando
- na direção oposta. Mas no primeiro caso
e no segundo
Que. vetor sempre direcionado ao longo do hodógrafo secante
para cima .

Se usarmos a expansão E por orts, então

A partir daqui dividindo (*) por
e indo até o limite
Para
nós conseguimos

Com base em (4), pode-se mostrar que as seguintes fórmulas são válidas:

(5)

(6)

- função escalar.

Prova (7).

Vamos agora examinar algumas propriedades
. Primeiro de tudo, vamos encontrar seu módulo:

.

Porque consideramos o arco do hodógrafo retificável, então
- é o comprimento do acorde, e
- comprimento do arco. É por isso

Que. o módulo da derivada da função vetorial de um argumento escalar é igual à derivada do arco hodográfico em relação ao mesmo argumento.

Corolário 1. Se - vetor unitário direcionado tangencialmente ao hodógrafo na direção de aumento , Que

Corolário 2. Se o comprimento do arco do hodógrafo for considerado o argumento da função vetorial , Que

(porque
)

Que. a derivada da função vetorial ao longo do comprimento do arco do hodógrafo é igual ao vetor unitário da tangente ao hodógrafo, direcionado ao aumento do comprimento do arco.

Corolário 3. Se o hodógrafo de uma função vetorial for considerado como a trajetória de um ponto, e - como o tempo de movimento, contado a partir de um determinado , Que
coincide em magnitude e direção com o vetor de velocidade de movimento
.

Na verdade, o valor escalar da velocidade é igual à derivada do caminho em relação ao tempo:

Além disso, o vetor direcionado tangencialmente à trajetória na direção do movimento, que corresponde à direção de aumento , ou seja corresponde à direção .

Que.
.

Vamos agora considerar
, cujo comprimento é constante,
, ou seja

(*)
Onde

Diferenciando (*), encontramos:

Aqueles.

Em particular, a derivada de um vetor de qualquer variável na direção da unidade Sempre
.

Deixe agora
o ângulo entre os raios da esfera unitária desenhados para os pontos
E
hodógrafo
. Então o comprimento do acorde
de um triângulo
será igual

A magnitude da derivada de um vetor de variável unitária é igual à velocidade angular de rotação deste vetor.

Quanto às funções escalares, o diferencial de uma função vetorial é escrito como

Mas mesmo assim

Curvatura de uma curva espacial.

Triedro acompanhante.

De acordo com o Corolário 2, para podemos escrever a fórmula:

Mudando de direção , associado a uma mudança na tangente à curva espacial, caracteriza a curvatura da curva. Como medida da curvatura de uma curva espacial, como para uma curva plana, toma-se o limite da razão entre o ângulo de adjacência e o comprimento do arco, quando

curvatura,
ângulo de adjacência,
comprimento do arco.

Do outro lado,
vetor unitário e seu vetor derivado é perpendicular a ele e seu módulo
Diferenciando Por e entrando
vetor unitário com direção , encontramos:

Vetor
vetor de curvatura de uma curva espacial. Sua direção, perpendicular à direção tangente, é a direção normal da curva espacial. Mas uma curva espacial tem em qualquer ponto um número infinito de normais, todas elas situadas num plano que passa por um determinado ponto da curva e é perpendicular à tangente num determinado ponto. Este plano é chamado de plano normal da curva espacial.

Definição. A normal da curva ao longo da qual o vetor de curvatura da curva é direcionado em um determinado ponto é a normal principal da curva espacial. Que.
vetor normal principal unitário.

Vamos agora construir o terceiro vetor unitário igual ao produto vetorial E

Vetor , como também perpendicular aqueles. está no plano normal. Sua direção é chamada de direção da binormal da curva espacial em um determinado ponto. Vetor
E constituem um trio de vetores unitários mutuamente perpendiculares, cuja direção depende da posição do ponto na curva espacial e varia de ponto a ponto. Esses vetores formam os chamados. triângulo acompanhante (triedro de Frenet) de uma curva espacial. Vetor
E formam um triplo à direita, assim como os vetores unitários
no sistema de coordenadas correto.

Tomado em pares
defina três planos que passam pelo mesmo ponto da curva e formam as faces do triângulo acompanhante. Ao mesmo tempo E determinar o plano osculante (o arco de uma curva na vizinhança de um determinado ponto é o arco de uma curva plana no plano osculante com uma precisão de ordem superior);

E - plano de endireitamento;

E - plano normal.

Equações tangentes, normais e binormais.

Equações dos planos do triângulo acompanhante.

Sabendo
E , ou quaisquer vetores não unitários colineares a eles T, N E B Vamos derivar as equações nomeadas nesta seção.

Para este efeito em equação canônica direto

e na equação do plano que passa por um determinado ponto

levar para
coordenadas do ponto selecionado na curva, por
ou respectivamente para
pegue as coordenadas dos vetores
ou
, que determina a direção da linha desejada ou normal ao plano desejado:

ou - para um plano tangente ou normal,

ou - para o plano principal normal e de endireitamento,

ou - para plano binormal e osculante.

Se a curva for dada pela equação vetorial
ou
então para o vetor
direcionado tangencialmente pode ser tomado

Para encontrar
E vamos primeiro encontrar a decomposição
por vetores
Anteriormente (Corolário 1) descobrimos que
Diferenciando por , obtemos:

Mas, porque

Vamos agora multiplicar vetorialmente E

(*)

Com base em (*) por vetor , tendo uma direção binormal, poderíamos pegar o vetor

Mas então, por
podemos pegar o produto vetorial destes últimos:

Que. em qualquer ponto de uma curva arbitrária podemos determinar todos os elementos do triângulo acompanhante.

Exemplo. Equação da tangente, normal e binormal à hélice direita em qualquer ponto.

Tangente

Casa normal

Binormal

Deixemos o conjunto de valores da função vetorial do argumento escalar ser reduzido a uma origem comum no ponto 0. Vamos combinar a origem do sistema de coordenadas cartesianas com este ponto. Então, qualquer vetor pode ser expandido em vetores unitários

Assim, especificar uma função vetorial de um argumento escalar significa especificar três funções escalares Quando o valor do argumento muda, o final do vetor descreverá uma curva no espaço, que é chamada de hodógrafo vetorial

Seja um valor próximo para Então a derivada de uma função vetorial para um argumento escalar é chamada

Nº 17 Velocidade e aceleração de um ponto em movimento curvilíneo

Velocidade

A velocidade é apresentada como uma característica do movimento de um ponto material. A velocidade é uma grandeza vetorial caracterizada tanto pela velocidade do movimento (magnitude do vetor velocidade) quanto por sua direção (direção do vetor velocidade) em no momento tempo. Deixar ponto material move-se ao longo de alguma trajetória curvilínea, e no tempo t corresponde ao vetor de raio r0 (Fig. 1). Em um curto período de tempo Δt, o ponto percorrerá Δs e ao mesmo tempo receberá um deslocamento elementar (infinitesimal) Δr.

Vetor de velocidade média é chamada de razão entre o incremento Δr do vetor raio de um ponto e o intervalo de tempo Δt:

A direção do vetor velocidade média coincide com a direção de Δr. Com uma diminuição infinita em Δt, a velocidade média tende para um valor denominado velocidade instantânea v:

Isso significa que a velocidade instantânea v é uma grandeza vetorial igual à primeira derivada do vetor raio do ponto móvel em relação ao tempo. Porque no limite, a secante coincide com a tangente, então o vetor velocidade v é direcionado tangente à trajetória na direção do movimento (Fig. 2).

Figura 2

À medida que Δt diminui, Δs se aproximará cada vez mais de |Δr|, então o módulo de velocidade instantânea

Isto significa que o valor absoluto da velocidade instantânea é igual à primeira derivada do caminho em relação ao tempo:

Com movimento irregular, o módulo da velocidade instantânea é diferente em momentos diferentes. Neste caso, use a quantidade escalar - velocidade média de movimento irregular:

Se integrarmos a expressão ds=vdt ao longo do tempo no intervalo de t a t+Δt (ver fórmula (2)), encontraremos o comprimento do caminho percorrido pelo ponto durante o tempo Δt:

No caso de movimento uniforme, o valor numérico da velocidade instantânea é constante; Então a expressão (3) assumirá a forma

O comprimento do caminho percorrido por um ponto durante o período de t1 a t2 é dado pela integral

ACELERAÇÃO

Ao dirigir de forma irregular, muitas vezes é necessário saber com que rapidez a velocidade muda ao longo do tempo. Uma quantidade física que caracteriza a taxa de mudança na velocidade em magnitude e direção é chamada de aceleração. Consideremos o movimento plano - movimento em que as trajetórias de cada ponto do sistema em consideração estão no mesmo plano. Seja o vetor v a velocidade do ponto A no tempo t. Durante o tempo Δt, o ponto moveu-se para a posição B e recebeu uma velocidade diferente de v tanto em magnitude quanto em direção e igual a v1 + Δv. Vamos mover o vetor v1 para o ponto A e encontrar Δv (Fig. 1).

A aceleração média do movimento irregular no intervalo de t a t+Δt é uma grandeza vetorial igual à razão entre a mudança na velocidade Δv e o intervalo de tempo Δt:

A aceleração instantânea a (aceleração) de um ponto material no tempo t será uma grandeza vetorial:

igual à primeira derivada da velocidade em relação ao tempo.

Vamos decompor o vetor Δv em duas componentes. Para isso, a partir do ponto A (Fig. 1) na direção da velocidade v, traçamos o vetor AD, cujo módulo é igual a v1. Obviamente, o vetor CD igual a Δvτ determina a mudança na velocidade ao longo do tempo Δt módulo: Δvτ=v1-v. A segunda componente Δvn do vetor Δv caracteriza a mudança na velocidade ao longo do tempo Δt na direção.

Componente tangencial da aceleração:

isto é, é igual à primeira derivada em relação ao tempo do módulo de velocidade, determinando assim a taxa de variação da velocidade no módulo.

Estamos procurando o segundo componente da aceleração. Assumimos que o ponto B está muito próximo do ponto A, então Δs pode ser considerado um arco de círculo de algum raio r, ligeiramente diferente da corda AB. O triângulo AOB é semelhante ao triângulo EAD, do qual segue Δvn/AB=v1/r, mas como AB=vΔt, então

No limite em Δt→0 obtemos v1→v.

Porque v1 → v, o ângulo EAD tende a zero, e como triângulo EAD é isósceles, então o ângulo ADE entre v e Δvn tende a um ângulo reto. Consequentemente, em Δt→0 os vetores Δvn e v tornam-se mutuamente perpendiculares. Porque o vetor velocidade é direcionado tangencialmente à trajetória, então o vetor Δvn, perpendicular ao vetor velocidade, é direcionado ao centro de curvatura da trajetória do ponto. O segundo componente da aceleração, igual a

é chamada de componente normal da aceleração e é direcionada ao longo de uma linha reta perpendicular à tangente à trajetória (chamada de normal) ao centro de sua curvatura (portanto, também é chamada de aceleração centrípeta).

Aceleração total corpo é a soma geométrica dos componentes tangencial e normal (Fig. 2):

Isso significa que o componente tangencial da aceleração é uma característica da taxa de variação da velocidade em magnitude (direcionada tangencialmente à trajetória), e o componente normal da aceleração é uma característica da taxa de variação da velocidade na direção (direcionada para o centro de curvatura da trajetória). Dependendo dos componentes tangencial e normal da aceleração, o movimento pode ser classificado da seguinte forma:

1)aτ=0, an=0 - movimento retilíneo uniforme;

2)aτ=an=const, аn=0 - movimento retilíneo uniforme. Com esse tipo de movimento

Se o tempo inicial t1 = 0, e a velocidade inicial v1 = v0, então, denotando t2=t e v2 = v, obtemos a=(v-v0)/t, a partir do qual

Tendo integrado esta fórmula no intervalo de zero a um momento arbitrário de tempo t, descobrimos que o comprimento do caminho percorrido por um ponto no caso de movimento uniformemente variável

3)aτ=f(t), an=0 - movimento retilíneo com aceleração variável;

4)aτ=0, an=const. Quando aτ=0, a velocidade não muda em valor absoluto, mas muda em direção. Da fórmula an=v2/r segue-se que o raio de curvatura deve ser constante. Portanto, o movimento circular é um movimento curvilíneo uniforme;

5)aτ=0, an≠0 movimento curvilíneo uniforme;

6)aτ=const, an≠0 - movimento curvilíneo uniforme;

7)aτ=f(t), an≠0 - movimento curvilíneo com aceleração variável.

Nº 18 Equações do plano tangente e normal à superfície

Definição. Seja dada uma função de duas variáveis ​​z =f(x,y) em um domínio D, M0(x0;y0) é um ponto interno do domínio D, M(x0+Δx;y+Δy) é um ponto em D “vizinho” M0.

Considere o incremento completo da função:

Se Δz for representado como:

onde A, B são constantes (independentes de Δx, Δy), - distância entre M e M0, α(Δ x,Δy) - infinitesimal em Δx 0, Δy 0; então a função z =f(x,y) é chamada diferenciável no ponto M0, e a expressão

é chamado de diferencial total da função z =f(x;y) no ponto M0.

Teorema 1.1. Se z =f(x;y) é diferenciável no ponto M0, então

Prova

Como em (1.16) Δx, Δy são infinitesimais arbitrários, podemos considerar Δy =0, Δx≠0, Δx 0, então

após o que de (1.16) segue

Da mesma forma, está provado que

e Teorema 1.1. comprovado.

Nota: a diferenciabilidade de z =f(x,y) no ponto M0 implica a existência de derivadas parciais. A afirmação inversa é falsa (a existência de derivadas parciais no ponto M0 não implica diferenciabilidade no ponto M0).

Como resultado, levando em consideração o Teorema 1.1, a fórmula (1.18) terá a forma:

Conseqüência. Uma função diferenciável no ponto M0 é contínua neste ponto (já que de (1.17) segue que para Δx 0, Δy 0: Δz 0, z(M) z(M0)).

Nota: Da mesma forma para o caso de três ou mais variáveis. A expressão (1.17) terá a forma:

Usando significado geométrico(Fig. 1.3) derivadas parciais e podemos obter a seguinte equação (1.24) do plano tangente πcass à superfície: z =f(x,y) no ponto C0(x0,y0,z0), z0=z(M ):

A partir de uma comparação de (1.24) e (1.21) obtemos o significado geométrico diferencial completo funções de duas variáveis:

Incremento do z aplicado quando o ponto C se move ao longo de um plano tangente do ponto C0 ao ponto

de onde é (1.24).

A equação da normal Lн à superfície: z = f(x,y) no ponto C0 é obtida como a equação de uma reta que passa por C0 perpendicular ao plano tangente:

Nº 19 Derivada direcional. Gradiente

Deixe uma função ser dada em algum domínio e período . Vamos desenhar um vetor a partir do ponto cujos cossenos de direção . No vetor, distante de seu início, considere um ponto, ou seja, .

Vamos supor que a função e suas derivadas parciais de primeira ordem são contínuas no domínio.

O limite da razão em é chamado de derivada da função no ponto na direção do vetor e é denotado, ou seja, .

Para encontrar a derivada de uma função em um determinado ponto na direção do vetor use a fórmula:

Onde – cossenos de direção do vetor , que são calculados pelas fórmulas:
.

Deixe uma função ser especificada em cada ponto de uma determinada região .

Um vetor cujas projeções nos eixos coordenados são os valores das derivadas parciais desta função no ponto correspondente é chamado de gradiente da função e é designado ou (leia “nabla u”): .

Nesse caso, dizem que um campo vetorial de gradientes está definido na região.

Para encontrar o gradiente de uma função em um determinado ponto use a fórmula: .

Nº 22 propriedades básicas da integral indefinida

Integral indefinido

onde F é a antiderivada da função f (no intervalo); C é uma constante arbitrária.

Propriedades básicas

1.

2.

3. Se Que

24)

25)

28)

Este método é utilizado nos casos em que o integrando é um produto ou quociente de funções heterogêneas. Neste caso, V’(x) é considerado a parte que é facilmente integrada.

29)

32) Decomposição de uma fração racional em frações simples.

Qualquer fração racional adequada
pode ser representado como a soma de um número finito de frações racionais simples do primeiro ao quarto tipo. Para decomposição
é necessário expandir o denominador em frações simples Qm(x) em fatores lineares e quadrados, para os quais você precisa resolver a equação:

- (5)

Teorema.Fração racional adequada
, Onde
, pode ser decomposto exclusivamente em uma soma de frações simples:

- (6)

(A 1 , A 2 , …, A k , B 1 , B 2 , …, B 1 , M 1 , N 1 , M 2 , M 2 , …, M s , N s – alguns números reais).

33) Decomposição de uma fração própria em frações simples com raízes complexas do denominador

Declaração do problema. Encontre a integral indefinida

1 . Vamos introduzir a seguinte notação:

Vamos comparar os graus do numerador e do denominador.

Se o integrando for uma fração racional imprópria, ou seja, grau do numeradorn maior ou igual à potência do denominadoreu , então primeiro selecionamos toda a parte da função racional dividindo o numerador pelo denominador:

Aqui o polinômio é o resto da divisão por e o grauPk(x) menos grauQm

2 . Vamos expandir a fração racional adequada

para frações elementares.

Se seu denominador for primo raízes complexas aqueles.

então a expansão tem a forma

3 . Para calcular coeficientes incertos,A1,A2,A3...B1,B1,B3... trazemos a fração do lado direito da identidade para um denominador comum, após o qual igualamos os coeficientes nas mesmas potênciasX nos numeradores à esquerda e à direita. Vamos pegar o sistema 2 S equações com 2 S desconhecido, que tem uma solução única.

4 Integramos frações elementares da forma

47) Se existe um limite finito I da soma integral como λ → 0, e não depende do método de escolha dos pontos ξ i, do método de particionamento do segmento, então esse limite é chamado de integral definida da função f ( x) sobre o segmento e é denotado da seguinte forma:

Neste caso, diz-se que a função f(x) é integrável em . Os números a e b são chamados de limites inferior e superior de integração, respectivamente, f (x) é o integrando, x é a variável de integração. Deve-se notar que não importa qual letra denota a variável de integração de uma integral definida

uma vez que alterar notações deste tipo não afeta de forma alguma o comportamento da soma integral. Apesar da semelhança na notação e na terminologia, certos e integrais indefinidas diferente

48) Teorema sobre a existência de uma integral definida

Vamos dividir o segmento em partes pelos pontos x1,x2,x3... então

Denotemos por deltaX o comprimento da i-ésima peça e pelo máximo desses comprimentos.

Vamos selecionar arbitrariamente um determinado ponto em cada segmento para que (é chamado de “ponto médio”), e compor

uma quantidade chamada soma integral

Vamos encontrar o limite agora

Definição. Se existe e não depende de

a) o método de dividir um segmento em partes e de

b) método de escolha do ponto médio,

é uma integral definida da função f(x) sobre o segmento .

A função f(x) é chamada neste caso integrável no intervalo. As quantidades aeb são chamadas de limites inferior e superior de integração, respectivamente.

50) Propriedades básicas de uma integral definida

1) Se o intervalo de integração for dividido em um número finito de intervalos parciais, então a integral definida obtida no intervalo é igual à soma das integrais definidas obtidas em todos os seus intervalos parciais.

2) o teorema do valor médio.

Deixe a função y = f (x) ser integrável no intervalo, m = min f (x) e M = max f (x), então existe tal número

Conseqüência.

Se a função y = f(x) for contínua no intervalo, então existe um número tal que.

3) Ao reorganizar os limites de integração, a integral definida muda seu sinal para o oposto.

4) Uma integral definida com os mesmos limites de integração é igual a zero.

5)Integração do módulo de função

Se a função f(x) for integrável, então seu módulo também será integrável no intervalo.

6)Integração da desigualdade

Se f(x) e q(x) são integráveis ​​em um intervalo e x pertence a

Que

7) Linearidade

O fator constante pode ser levado além do sinal da integral definida

se f(x) existe e é integrável no intervalo, A=const

Se a função y=f(x) for contínua em um intervalo e F(x) for qualquer uma de suas primitivas em (F’(x)=f(x)), então a fórmula é válida

Vamos, para calcular a integral de função contínua a substituição x=α(t) é feita.

1) A função x=α(t) e sua derivada x’=α’(t) são contínuas para t pertencentes a

2) O conjunto de valores da função x=α(t) em t pertence ao segmento

3) A α(c)=a e α(v)=b

Seja a função f(x) contínua no intervalo e tenha uma descontinuidade infinita em x=b. Se existir um limite, então ele é chamado de integral imprópria de segundo tipo e é denotado por.

Assim, por definição,

Se o limite do lado direito existir, então a integral imprópria converge. Se o limite especificado não existe ou é infinito, então dizem que a integral diverge.

Baixe em Depositfiles

GEOMETRIA DIFERENCIAL

EU. FUNÇÃO VETORIAL DO ARGUMENTO ESCALAR

Função vetorial (definição 1.1), métodos para especificá-la.

Vetor de raio e hodógrafo, especificação paramétrica do hodógrafo.

Derivada de uma função vetorial (Definição 1.6).

Significado geométrico da derivada de uma função vetorial.

Regras para diferenciação de funções vetoriais.

1.1. DEFINIÇÃO DE FUNÇÃO VETORIAL

Definição 1.1Se cada valor do argumento escalarvetor correspondente
espaço tridimensional R3 , então eles dizem que uma função vetorial (ou função vetorial) de um argumento escalar é dada no conjunto Xt .

Se no espaço R3 dado sistema cartesiano coordenadasSOBRE xyz , então a tarefa é uma função vetorial
,
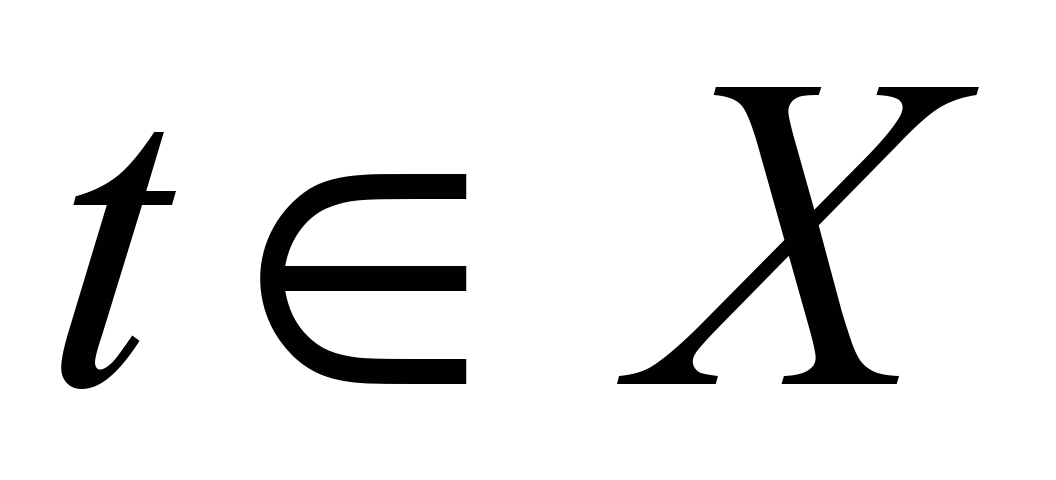é equivalente a especificar três funções escalaresX( t ), sim ( t ), z ( t ) – coordenadas vetoriais:

= { x ( t ), sim ( t ), z ( t )} (1.1)

ou , (1.2)

Onde
— vetores unitários coordenados.

1.2. LINHA ESPACIAL COMO HODÓGRAFO DO VETOR DE RAIO

Definição 1.2 Se o início de todos os vetores for ,colocados na origem, eles são chamados de vetores de raio.

Definição 1.3 A linha que é o lugar geométrico das extremidades dos vetores de raio , , é chamada de hodógrafo da função vetorial, e seu início comum é o pólo do hodógrafo.

Se o parâmetro t é o tempo e é o vetor raio do ponto móvel, então o hodógrafo da função é a trajetória do ponto móvel.

A equação do hodógrafo pode ser escrita na forma vetorial (1.2) ou na forma paramétrica:

(1.3)

Em particular, se a função vetorialcom uma mudança no argumento, apenas seu módulo muda, mas a direção não muda (), então o hodógrafo de tal função vetorial será um raio retilíneo emanando da origem; se apenas a direção do vetor mudar, mas sua magnitude permanecer inalterada (
), então o hodógrafo da função vetorial será uma curva localizada em uma esfera com centro no pólo e raio igual ao módulo constante do vetor.

Figura 1.

1.3. LIMITE, CONTINUIDADE E DERIVADA DA FUNÇÃO VETORIAL

Definição 1. 4 vetor é chamado de limite da função vetorialno
, Se

. (1.4)

Definição 1.5 A função vetorial é chamada contínuo em um pontot 0, se tiver um limite neste ponto igual ao valor da função vetorial neste ponto:

. (1.5)

Definição 1.6Derivada de uma função vetorial no ponto t é chamado de limite da razão entre o incremento de uma função vetorial e o incremento do argumento
no
:

(1.6)

1.4. SIGNIFICADO GEOMÉTRICO E MECÂNICO DA PRIMEIRA DERIVADA DA FUNÇÃO VETORIAL

O significado geométrico da primeira derivada da função vetorial do argumento escalar é que esta derivada é um novo vetor direcionado tangencialmente ao hodógrafo:
. Vamos mostrar.

Figura 2

Assumiremos que o hodógrafo da função vetorial em consideração é uma reta contínua que possui uma tangente em qualquer ponto.

Vamos dar o argumento t incremento, então geometricamente a razão
é algum vetor
, deitado na secante MM’. Quando este vetor gira e se transforma em um vetor
, deitado na tangente e direcionado para aumentart . Então o vetor

(1.7)

será um vetor tangente unitário orientado na direção do parâmetro crescentet .

Portanto, o vetor
pode ser tomado como um vetor de direção tangente à curva no ponto ), (ou
) e escreva a equação tangente na forma:

(1.8)

Se t – tempo, e — vetor raio de um ponto
, movendo-se em espaço tridimensional, então sobrea relação é chamada de velocidade média de um ponto no segmento [t; t+t].

Significado mecânicoa primeira derivada da função vetorial é que esta derivada representa a velocidade do ponto M no momentot :

Regras para diferenciação de funções vetoriais

Vamos provar a regra 1 usando as regras para subtrair vetores e dividir um vetor por um número:

A prova das demais regras é baseada na regra 1 e nas regras de operação com vetores.

Exemplo 1.1: Dada uma função vetorial.Construa seu hodógrafo e crie uma equação para sua tangente em um ponto arbitrário.

Solução. Para qualquer ponto ( x , sim , z ) vetor hodógrafo – funções que temos:x = custo ; sim = asint ; z = aliás e, portanto, para qualquer
igualdade valex 2 + sim 2 = um 2 , e a geratriz é paralela ao eixo Onça. Se o parâmetro t interpretado como tempo, então com movimento uniforme em torno de um círculo a projeção do final do vetor raio no planoOxi sua projeção no eixoonça se moverá de maneira uniforme e retilínea em velocidadeb . Em outras palavras, a aplicação de um ponto hodográfico de uma função vetorial cresce proporcionalmente ao ângulo de rotação de sua projeção no planoOxi . Portanto, o hodógrafo desejado terá o formato mostrado na Fig. 3 e é chamado de linha helicoidal. Para encontrar as tangentes ao hodógrafo (linha helicoidal), encontramos a derivada da função vetorial.

Solução. Desde, então

Exemplo 2. Considere, por exemplo, uma função de três variáveis f(X,no,z), tendo a seguinte tabela verdade:

Com a ordem lexicográfica dos vetores de valores variáveis  X n eles podem ser omitidos e a função será completamente especificada por sua própria vetor de valores de verdade f= (10110110).

Método matricial

A questão é que muitas variáveis  X n se divide em duas partes  no eu E  z n–m de tal forma que todos os valores verdade possíveis do vetor  no eu são plotados ao longo das linhas da matriz, e todos os valores verdade possíveis do vetor  z n-m- por colunas. Valores de verdade da função f em cada conjunto   n = ( 1 , ...,  eu ,  m+ 1 ,...,  n) colocado nas células formadas pela intersecção da linha ( 1 , ...,  eu) e coluna ( m+ 1 ,...,  n).

No Exemplo 2 discutido acima, no caso de variáveis ​​de particionamento ( x, y, z) em subconjuntos ( X) E ( sim, z) a matriz assume a forma:

	sim,z

Uma característica essencial do método matricial é que conjuntos completos de variáveis  X n, correspondentes a células vizinhas (vertical e horizontalmente), diferem em uma coordenada.

Especificando usando uma árvore binária completa

Para descrição n-função local f( X n) a propriedade da árvore binária de altura é usada n, que consiste no fato de que cada vértice pendente nele corresponde um a um a um determinado conjunto de valores vetoriais  X n. Conseqüentemente, este vértice suspenso pode receber o mesmo valor de verdade que a função tem neste conjunto f. Como exemplo (Fig. 1.3), apresentamos uma tarefa usando uma árvore binária da função ternária discutida acima f =(10110110).

A primeira linha de números atribuídos aos vértices suspensos da árvore denota o número lexicográfico do conjunto, a segunda - o próprio conjunto e a terceira - o valor da função nele.

Tarefa usandon - cubo de unidade dimensionalEM n

Desde os topos EM n também pode ser mapeado individualmente para o conjunto de todos os conjuntos  X n, Que n-função local f(X n) pode ser especificado atribuindo seus valores verdade aos vértices correspondentes do cubo EM n . A Figura 1.4 mostra a configuração da função f= (10110110) no cubo EM 3. Os valores verdade são atribuídos aos vértices do cubo.

Definição . Álgebra da lógica nomeie um conjunto de constantes e variáveis ​​booleanas junto com os conectivos lógicos introduzidos nelas.

Tarefa de fórmula

As funções de álgebra lógica podem ser especificadas como expressões analíticas.

Definição. Deixar X― alfabeto de variáveis ​​e constantes usadas em álgebra lógica; F― um conjunto de notações para todas as funções elementares e suas generalizações com números de variáveis ​​superiores a 2.

Fórmula sobre X,F(fórmula de álgebra lógica) vamos chamar todos os registros do formulário:

UM) X, Onde X X;

b) F 1 , F 1 &F 2 ,F 1 F 2 , F 1 F 2 , F 1  F 2 , F 1 F 2 ,F 1 F 2 ,F 1 F 2 , Onde F 1 , F 2 - fórmulas terminadas X, F;

V) h(F 1 , … ,F n ), Onde n > 2, F 1 ,… ,F n- fórmulas terminadas X,F, h ― denotação da função de limiar generalizada de F .

Como segue da definição, para funções elementares de duas casas é usada a forma de notação infixa, na qual o símbolo funcional é colocado entre os argumentos para negação e funções generalizadas, a forma de notação prefixada é usada, na qual o símbolo funcional; é colocado antes da lista de argumentos.

Exemplo 3.

1. Expressões X(noz); ( x, sim, z  você) são fórmulas da álgebra da lógica, pois satisfazem a definição dada acima.

2. Expressão  X (no z) não é uma fórmula de álgebra lógica porque a operação  foi aplicada incorretamente .

Definição. A função implementada pela fórmula F, é a função obtida substituindo os valores das variáveis ​​​​em F. Vamos denotar isso f(F).

Exemplo 4. Considere a fórmula F=xy (Xz). Para construir a tabela verdade da função implementada, é necessário realizar a multiplicação lógica sequencialmente, levando em consideração a força dos conectivos lógicos xy, então a implicação ( Xz), em seguida, adicione os valores verdade resultantes módulo 2. O resultado das ações é mostrado na tabela:

				X z

A representação estereotipada de funções permite avaliar a priori muitas propriedades das funções. A transição de uma tarefa estereotipada para uma tabela verdade sempre pode ser realizada por substituições sucessivas de valores verdade em funções elementares incluídas na fórmula. A transição reversa é ambígua, pois a mesma função pode ser representada por fórmulas diferentes. Requer consideração separada.

Definição 1. Um vetor r é chamado de função vetorial do argumento escalar t se cada valor do escalar da faixa de valores permitidos corresponder a um determinado valor do vetor r. Vamos escrevê-lo assim: Se o vetor r. r é uma função do argumento escalar t, então as coordenadas x, y, z do vetor r também serão funções do argumento t: Função vetorial do argumento escalar. Hodógrafo. Limite e continuidade da função vetorial de um argumento escalar Por outro lado, se as coordenadas do vetor g são funções de t%, então o próprio vetor g será uma função de t: Assim, especificar a função vetorial r(f) é. equivalente a especificar três funções escalares y(t), z( t). Definição 2. O hodógrafo de uma função vetorial r(t) de um argumento escalar é o lugar geométrico dos pontos que descreve o final do vetor r(*) quando o escalar t muda, quando o início do vetor r(f) é colocado em um ponto fixo O no espaço (Fig. I). Hodógrafo por causa do movimento do vetor bigode r = g(*) Fig. 1 ponto de queima será a trajetória L deste próprio ponto. O hodógrafo de velocidade v = v(J) deste ponto será alguma outra linha L\ (Fig. 2). Portanto, se um ponto material se move em círculo com velocidade constante |v| = const, então seu hodógrafo de velocidade também é um círculo com centro no ponto 0\ e raio igual a |v|. Exemplo 1. Construa um hodógrafo do vetor r = ti + t\ + t\. Solução. 1. Esta construção pode ser feita ponto a ponto, formando uma tabela: Fig. 3 2i Você pode fazer o mesmo. Denotando as coordenadas do vetor V por x, y, z, teremos Hts E a chave dessas equações é o parâmetro 1Y obtemos as equações das superfícies y - z = x1, cuja linha de interseção L determinará o hodógrafo do vetor z() (Fig. 3). D> Tarefas para. Construa hodógrafos de vetores: Deixe a função vetorial r = argumento escalar t ser definida em uma certa vizinhança do valor a do argumento t, exceto, talvez, para o mesmo valor, extensão 1. O vetor constante À é chamado de limite de o vetor r(t) quando, se para qualquer e > 0 existe b > 0 tal que para todo t φ que satisfaça a condição 11, a desigualdade é válida. Como na análise convencional, escreva limr(0=A. Fig. 4 Geometricamente. , isso significa que o vetor) como t -* to tende ao vetor E tanto em comprimento quanto em direção (Fig. 4). Definição 2. Diz-se que o vetor a(£) é infinitesimal em t -» to se a(£) tem um limite em t -* to e esse limite é igual a zero: Função vetorial de um argumento escalar. Hodógrafo. O limite e a continuidade de uma função vetorial de um argumento escalar ou, o que é o mesmo, para qualquer e existe 6 > 0 tal que para todo t Ф que satisfaça a condição, a desigualdade |a(£)| Exemplo 1. Mostre que o vetor é um vetor infinitamente escarlate para t -* 0. Solução. Temos onde fica claro que se para qualquer e 0 tomamos 6 = ~, então em -0| vamos marcar |. De acordo com a definição, isso significa que a(t) é um vetor infinito em t 0. 1> problemas para resolver r independentemente Mostre que o limite do módulo de um vetor é igual ao módulo do seu limite se este último limite. existe. . Prove que para que a função vetorial r(*) tenha um limite A em to, é necessário e suficiente que r(pode ser representado como uma função vetorial de um argumento escalar. Hodógrafo. Limite e continuidade de uma função vetorial de um argumento escalar de a( t) é um vetor infinito para t -* t0 14. A função vetorial a+ b(*) é contínua para t = t0. também são contínuas para t - to ? 15. Prove que se a( são funções vetoriais contínuas, então seu produto escalar (a(*),b(f)) e produto vetorial |a(f),b(t)] também são contínuos.