Equação característica. Raízes da equação característica. Constantes de tempo. Tempo de transição. Métodos para compilar uma equação característica Por que você precisa de uma equação característica

A equação característica é compilada para o circuito após a comutação. Pode ser obtido das seguintes maneiras:

• diretamente com base em uma equação diferencial da forma (2) (ver aula nº 24), ou seja, excluindo do sistema de equações que descrevem o estado eletromagnético do circuito baseado na primeira e segunda leis de Kirchhoff, todas as quantidades desconhecidas, exceto uma, em relação à qual a equação (2) é escrita;
• usando uma expressão para a impedância de entrada de um circuito de corrente senoidal;
• com base na expressão do determinante principal.

De acordo com o primeiro método, na aula anterior, foi obtida uma equação diferencial relativa à tensão no capacitor para um circuito R-L-C em série, com base na qual é escrita a equação característica.

Deve-se notar que, como o circuito linear é coberto por um único processo transitório, as raízes da equação característica são comuns a todos os componentes livres das tensões e correntes dos ramos do circuito, cujos parâmetros estão incluídos na equação característica. Portanto, de acordo com o primeiro método de composição de uma equação característica, qualquer variável pode ser escolhida como a variável em relação à qual é escrita.

Consideremos a aplicação do segundo e terceiro métodos de composição da equação característica usando o exemplo do circuito da Fig. 1.

A composição da equação característica usando o método da resistência de entrada é a seguinte:

está gravado impedância de entrada Circuitos CA;

jw é substituído pelo operador p;

a expressão resultante é igual a zero.

Equação

coincide com o característico.

Deve-se enfatizar que a resistência de entrada pode ser escrita em relação ao ponto de interrupção de qualquer ramo do circuito. Neste caso, a rede ativa de dois terminais é substituída por uma passiva por analogia com o método do gerador equivalente. Este método de composição da equação característica pressupõe a ausência de ramos acoplados magneticamente no circuito; se houver, é necessário proceder à sua desvinculação preliminar.

Para o circuito da Fig. 1 em relação aos terminais de origem

.

Substituindo jw por p e igualando a expressão resultante a zero, escrevemos

.

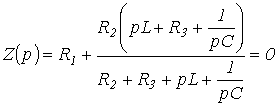
(1)

Ao compilar uma equação característica baseada na expressão do determinante principal, o número equações algébricas, com base no qual está escrito, é igual ao número de componentes de corrente livre desconhecidos. Algebrização do sistema original de integração equações diferenciais, compilado, por exemplo, com base nas leis de Kirchhoff ou utilizando o método das correntes de loop, é realizado substituindo os símbolos de diferenciação e integração, respectivamente, pela multiplicação e divisão pelo operador p. A equação característica é obtida igualando o determinante escrito a zero. Como a expressão do determinante principal não depende do lado direito do sistema de equações não homogêneas, ela pode ser compilada com base em um sistema de equações escritas para correntes totais.

Para o circuito da Fig. 1 sistema algebrizado de equações baseado no método das correntes de loop tem a forma

Daí a expressão para o principal determinante deste sistema

Igualando D a zero, obtemos um resultado semelhante a (1).

Metodologia geral para cálculo de processos transitórios pelo método clássico

Em geral, a metodologia de cálculo de processos transitórios pelo método clássico inclui as seguintes etapas:

Exemplos de cálculo de processos transitórios usando o método clássico

1. Processos transitórios em Correntes RL quando conectado a uma fonte de tensão

Tais processos ocorrem, por exemplo, ao conectar eletroímãs, transformadores, motores elétricos, etc. a uma fonte de energia.

Vamos considerar dois casos:

De acordo com o método considerado para a corrente no circuito da Fig. 2 pode ser escrito

Equação característica

daí a constante de tempo .

Por isso,

.

(5)

Substituindo (4) e (5) na relação (3), escrevemos

.

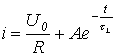De acordo com a primeira lei da comutação. Então

,

Assim, a corrente no circuito durante o processo transitório é descrita pela equação

,

e a tensão no indutor é dada por

.

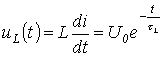O aspecto qualitativo das curvas e correspondente às soluções obtidas é apresentado na Fig. 3.

Para o segundo tipo de fonte, o componente forçado é calculado pelo método simbólico:

,

A expressão da componente livre não depende do tipo de fonte de tensão. Por isso,

.

Desde então

Assim, finalmente obtemos

.

(6)

A análise da expressão resultante (6) mostra:

Se for significativo em magnitude, então durante meio período o componente livre não diminui significativamente. Neste caso, o valor máximo da corrente transitória pode exceder significativamente a amplitude da corrente em estado estacionário. Como pode ser visto na Fig. 4, onde

, a corrente máxima ocorre após aproximadamente . No limite em .

Assim, para um circuito linear, o valor máximo da corrente transitória não pode ultrapassar o dobro da amplitude da corrente forçada: .

Da mesma forma para um circuito linear com um capacitor: se no momento da comutação a tensão forçada for igual ao seu valor de amplitude e a constante de tempo do circuito for suficientemente grande, então após cerca de meio período a tensão no capacitor atinge seu valor máximo , que não pode exceder o dobro da amplitude da tensão forçada: .

2. Processos transitórios ao desconectar o indutor da fonte de alimentação

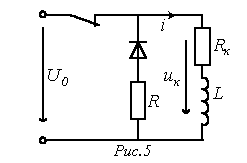
Quando a chave é aberta no circuito da Fig. 5 componente forçado da corrente através do indutor.

Equação característica

,

onde E .

De acordo com a primeira lei da comutação

.

Assim, a expressão para a corrente transitória é

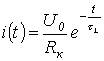
e tensão no indutor

.

(7)

A análise (7) mostra que quando circuitos contendo elementos indutivos são abertos, podem ocorrer grandes sobretensões que, sem medidas especiais, podem danificar o equipamento. Na verdade, quando O módulo de tensão no indutor no momento da comutação será muitas vezes maior que a tensão da fonte: . Na ausência de um resistor de extinção R, a tensão especificada é aplicada aos contatos de abertura da chave, resultando em um arco entre eles.

3. Carregando e descarregando um capacitor

Quando a chave é movida para a posição 1 (ver Fig. 6), inicia-se o processo de carregamento do capacitor:

.

Componente de tensão forçada em um capacitor.

Da equação característica

a raiz é determinada . Daí a constante de tempo.

O modo livre do circuito não depende de fontes de energia, é determinado apenas pela estrutura do circuito e pelos parâmetros de seus elementos. Segue-se disso que as raízes da equação característica p1, p2,…, pn serão as mesmas para todos funções variáveis(correntes e tensões).

A equação característica pode ser construída usando vários métodos. O primeiro método é clássico, quando a equação característica é compilada estritamente de acordo com a equação diferencial de acordo com o esquema clássico. Ao calcular processos transitórios em esquema complexo um sistema de equações diferenciais “m” é compilado de acordo com as leis de Kirchhoff para o diagrama de circuito após a comutação. Como as raízes da equação característica são comuns a todas as variáveis, a solução do sistema de equações diferenciais é realizada em relação a qualquer variável (opcional). Como resultado da solução, obtém-se uma equação diferencial não homogênea com uma variável. Componha uma equação característica de acordo com a equação diferencial resultante e determine suas raízes.

Exemplo. Elabore uma equação característica e determine suas raízes para as variáveis ​​no diagrama da Fig. 59.1. Os parâmetros dos elementos são especificados de forma geral.

Sistema de equações diferenciais segundo as leis de Kirchhoff:

Resolvamos o sistema de equações para a variável i3, como resultado obtemos uma equação diferencial não homogênea:

A segunda maneira de compilar uma equação característica é igualar a zero o principal determinante do sistema de equações de Kirchhoff para as variáveis ​​​​de componentes livres.

Deixe o componente livre de uma corrente arbitrária ter a forma iksv = Аkept, então:

O sistema de equações para as componentes livres é obtido a partir do sistema de equações diferenciais de Kirchhoff substituindo as derivadas das variáveis ​​pelo fator p, e as integrais por 1/p. Para o exemplo em consideração, o sistema de equações para componentes livres tem a forma:

Equação característica e sua raiz:

A terceira maneira de compilar uma equação característica (engenharia) é igualar a resistência do operador de entrada do circuito a zero em relação a qualquer um de seus ramos.

A resistência do operador de um elemento é obtida a partir de sua resistência complexa simplesmente substituindo o fator jω por p, portanto

Para o exemplo em questão:

O terceiro método é o mais simples e econômico, por isso é mais frequentemente utilizado no cálculo de processos transitórios em circuitos elétricos.

As raízes da equação característica caracterizam o processo transitório livre em um circuito sem fontes de energia. Este processo ocorre com perdas de energia e, portanto, decai com o tempo.

No caso geral, a ordem da equação diferencial que descreve o processo transitório no circuito e, conseqüentemente, o grau da equação característica e o número de suas raízes são iguais ao número de independentes condições iniciais, ou o número de dispositivos independentes de armazenamento de energia (bobinas L e capacitores C).

Se o diagrama de circuito contém capacitores conectados em paralelo C1, C2,... ou bobinas conectadas em série L1, L2,..., então, ao calcular processos transitórios, eles devem ser substituídos por um elemento equivalente SE = C1 + C2+... ou LE = L1 + L2+... Por isso, visão geral

soluções para qualquer variável no cálculo de um processo transitório só podem ser compiladas a partir de uma análise do diagrama de circuito, sem compilar e resolver um sistema de equações diferenciais.

) Para o exemplo discutido acima. = ||UM||um sim n

1 subtraindo o valor λ dos elementos diagonais. Este determinante é um polinômio em relação a X - um polinômio característico. Quando aberto, X. u. está escrito assim: Onde = S1 + um 11 +... um 22 Ana - chamado traço de matriz, S2 um sim- a soma de todos os menores maiores de 2ª ordem, ou seja, menores da forma i k), etc., e S Para o exemplo discutido acima.- determinante da matriz um sim. Raízes de H. você. λ 1 , λ 2 ,..., λ Para o exemplo discutido acima. são chamados de autovalores da matriz . Para uma matriz simétrica real, bem como para uma matriz Hermitiana, todos λ k . Para uma matriz simétrica real, bem como para uma matriz Hermitiana, todos λ são reais, uma matriz assimétrica real tem todos λ . Para uma matriz simétrica real, bem como para uma matriz Hermitiana, todos λ| = 1.

números puramente imaginários; no caso de uma matriz ortogonal real, bem como de uma matriz unitária, todos |λ

Hu. encontrado em uma ampla variedade de áreas da matemática, mecânica, física e tecnologia. Na astronomia, ao determinar as perturbações seculares dos planetas, eles também chegam às equações químicas; daí o segundo nome para X. u. - uma equação milenar.

2) H. você. equação diferencial linear com coeficientes constantesλ um 0 (sim) + n (um 1 ano) +... + n-1 + um n-1 ano" = 0

qualquer Equação algébrica obtida a partir de uma determinada equação diferencial após alterar a função no

2) H. você. equação diferencial linear com coeficientes constantesλ um sim + e suas derivadas pelas potências correspondentes de λ, ou seja, a equaçãoλ um 1 + ... + n-1 um n-1 + um n-1 ano" = 0.

você" Equação algébrica obtida a partir de uma determinada equação diferencial após alterar a função = Esta equação é obtida encontrando uma solução particular da forma λ se X

para uma dada equação diferencial. Para um sistema de equações diferenciais lineares

Hu. escrito usando um determinante Hu. matrizes =

UM Grande Enciclopédia Soviética. 1969-1978 .

. - M.: Enciclopédia Soviética

Veja o que é uma “Equação Característica” em outros dicionários: Em muitos casos, ocorrendo em sistemas, são descritos por um sistema de equações diferenciais lineares ordinárias com coeficientes constantes, que em um caso bastante geral podem ser reduzidos à equação diferencial ... Enciclopédia de tecnologia

Uma equação algébrica da forma: O determinante nesta fórmula é obtido a partir do determinante da matriz subtraindo o valor x dos elementos diagonais; representa um polinômio em x e é chamado de polinômio característico... Grande Dicionário Enciclopédico

equação característica- - [V.A. Dicionário Inglês-Russo de proteção de relé] Tópicos proteção de relé EN equação característica ... Guia do Tradutor Técnico

Equação algébrica da forma. O determinante nesta fórmula é obtido a partir do determinante da matriz x de elementos diagonais; é um polinômio em x e é chamado de polinômio característico. * * * CARACTERÍSTICA… … Dicionário Enciclopédico

equação característica- būdingoji lygtis statusas T sritis automatika atitikmenys: engl. equação característica; equação de desempenho vok. caráter característico Gleichung, f; Stammgleichung, f rus. equação característica, n pranc. equação característica, f … Terminų žodynas automático

equação característica- būdingoji lygtis statusas T sritis fizika atitikmenys: engl. equação característica; equação de desempenho vok. Charakteristische Gleichung, f rus. equação característica, n pranc. equação característica, f … Fizikos terminų žodynas

equação característica Enciclopédia "Aviação"

equação característica- equação característica. Em muitos casos, os processos físicos que ocorrem nos sistemas são descritos por um sistema de equações diferenciais lineares ordinárias com coeficientes constantes, que num caso bastante geral podem ser reduzidos... Enciclopédia "Aviação"

Equação secular, ver art. Polinômio característico... Enciclopédia Matemática

Um polinômio característico é um polinômio que determina os autovalores de uma matriz. Outro significado: O polinômio característico de uma recorrente linear é um polinômio. Conteúdo 1 Definição ... Wikipedia

Livros

• Anéis de Lie característicos e equações integráveis ​​não lineares, Zhiber A.V.. O livro é dedicado a uma apresentação sistemática da abordagem algébrica para o estudo de equações diferenciais parciais integráveis ​​não lineares e seus análogos discretos, com base no conceito...

A equação característica tem a forma:

Para determinar o tipo de componente livre, é necessário compor e resolver a equação característica: z(p) = 0. Para escrever a equação característica, é necessário desenhar um diagrama no qual todas as fontes de fem e corrente devem ser substituídas por seu próprio interno resistência e resistência tome a indutância e a capacitância respectivamente iguais a Pl e , então é necessário quebrar qualquer ramo deste circuito, anotar sua resistência inicial em relação aos pontos de ruptura, igualá-la a zero, resolver e determinar as raízes de p, se as raízes acabar sendo real negativo, então o componente livre da função desejada:

,onde m é o número de raízes da equação;

Raízes; - permanentemente integrado.

Se as raízes da equação de caracteres forem conjugadas complexas, então o estado livre terá a forma:

onde está a frequência das vibrações livres;

A fase inicial de oscilações livres.

8.Tempo de transição. Determinação de praticamente t pp. Cálculo do tempo do processo de transição.

O tempo do processo transitório depende do coeficiente de atenuação. O valor inverso é chamado de constante de tempo e é. tempo, durante qual o valor do componente livre do processo transitório diminuirá em e=2,72 vezes. O valor depende do circuito e dos parâmetros. Portanto, para um circuito com. conexão serial r e L = , e em conexão em série

95% de conclusão do processo de transição 3.

A maneira mais fácil de construir as curvas dos componentes livres do processo transitório é definir os valores de tempo t como 0, ,2.....Se houver várias raízes reais, então a curva resultante é obtida somando os ordenadas dos termos individuais (Fig. 1.)

Figura 1:

9.10, Processo transitório em r, C – circuitos quando conectados a uma fonte Tensão CC. Realize a análise pelo método clássico; dê expressões analíticas para U C (t); iC(t); gráficos. (Método clássico).

A equação de estado do circuito rC após a comutação é a seguinte:

(1) ou RC (2)

Sua solução:

A capacidade C após fechar a chave em t será cobrada para um valor estável.

Como as condições iniciais são zero, de acordo com a lei de comutação em t=0, ou 0=A, de onde A=-E.

A solução da equação (2) terá a forma:

Corrente do circuito i(t)=C

Figura 1.

Figura 2.

Gráficos de mudanças na tensão e corrente i(t) são mostrados nas Figuras 1 e 2. Pelas figuras pode-se observar que a tensão no capacitor aumenta exponencialmente de 0 a E, enquanto a intensidade da corrente no momento da comutação atinge abruptamente o valor E/r, e depois diminui para zero.

11.12.Processo transitório em r, C – circuitos quando conectados a uma fonte de tensão senoidal. Realize a análise pelo método clássico; dê expressões analíticas para U C (t); iC(t); gráficos. (Método clássico).

A equação de estado do circuito rC no modo transitório é a seguinte

RC .

Solução para esta equação:

Componente gratuito

onde =rC

Como o circuito é linear, então com efeito senoidal e em estado estacionário, a tensão no capacitor também mudará de acordo com uma lei senoidal com a frequência do efeito de entrada. Portanto, para determinar = usaremos o método de amplitudes complexas. :

;

Considerando que j= , obtemos:

Constante de integração A do componente livre

Vamos descobrir a partir das condições iniciais do circuito levando em consideração a lei de comutação:

.Em t=0 a última expressão tem a forma

Onde A=-

Somando as componentes e, obtemos a expressão final para a tensão no capacitor no modo transitório:

= + = - (1)

A análise da expressão (1) mostra que o processo transitório no circuito rC sob influência senoidal depende da fase inicial da fem da fonte no momento da comutação e da constante de tempo do circuito rC.

Se , então =0 e um estado estacionário ocorrerá no circuito imediatamente após a comutação, ou seja,

Quando tensão = -, ou seja, A tensão no capacitor imediatamente após a comutação pode atingir quase o dobro do valor do sinal positivo e, então, aproximar-se gradualmente de =.

A diferença de fase levará a equação (1) à forma:

A diferença entre este modo e o anterior é que a tensão no capacitor imediatamente após a comutação pode atingir quase o dobro do valor negativo.

Para o circuito Rc considerado com uma fonte de corrente senoidal em estado estacionário, a fase inicial tensão de entrada não desempenha qualquer papel, mas no processo de transição a sua influência é significativa.

13.Processo transitório em r, L, C – circuitos quando conectados a uma fonte de tensão constante. Processo em lote. Expressões analíticas para i(t), gráficos. (Método clássico).

As raízes são reais, negativas, diferentes.

I(t)=I boca +A1e p 1 t +A2e p 2 t

O processo é periódico:

t=0 (i(0)=A1+A2; A1=-A2

{

t=0 eu l (0)*r+L +Uc(0)=E A1=-A2= ()

eu eu (t)= ( )

14.Processo transitório em r, L, C – circuitos quando conectados a uma fonte de tensão constante. Processo crítico. Expressões analíticas para i(t), gráficos. (Método clássico).

eu l (t)=i boca +(B1+B2*t)*

t=0: eu l (0)=β1=0

Se as raízes forem reais, negativas, iguais, então o processo é crítico.

15.Processo transitório em r, L, C – circuitos quando conectados a uma fonte de tensão constante. Processo oscilatório. Expressão analítica para i(t), gráficos. (Método clássico).

P t = -δ±j*ω St ω St =

As raízes são reais negativas, algumas conjugadas complexas.

eu l (t)=i boca A1e - δt *sin(ω St t+ψ)

i l (t)=i boca +(M*cos ω luz t+N*sin ω luz t)*

eu eu (t)= * = *

16. Processo transitório em r, L, C – circuitos quando conectados a uma fonte de tensão senoidal. Processo aperiódico. Expressão analítica para i(t), gráficos. (Método clássico).

R(t)=E máx *sin(ωt+ψ)

2.

No número clássico de equações, neste caso, é igual ao número de ramificações do circuito

O método encontra uma solução na forma da soma de uma solução geral e de uma solução particular. O cálculo do processo transitório é descrito por um sistema de equações diferenciais ordinárias compiladas por um dos métodos de cálculo para valores instantâneos de funções de tempo. A solução para cada variável deste sistema é encontrada na forma da soma das soluções gerais e particulares. Para compilar uma equação, podem ser utilizados: um método baseado na aplicação das leis de Kirchhoff, o método dos potenciais nodais, o método das correntes de loop, etc. Por exemplo, um sistema de equações diferenciais compilado após a comutação de acordo com a primeira e a segunda leis de Kirchhoff tem a forma:

Por exemplo,

O número de equações neste caso é igual ao número de ramificações do circuito. Seja necessário encontrar a corrente i k em um ramal com número K. Eliminando as correntes dos ramos em sequência, obtemos como resultado a corrente i k e suas derivadas até a ordem n:

A ordem da equação diferencial n é determinada pelo número de elementos reativos independentes do circuito (m). Normalmente n=m, mas dependendo do método de conexão pode ser que n

Os elementos capacitivos conectados em série podem ser substituídos por um elemento, assim como os elementos indutivos conectados em paralelo podem ser substituídos por um equivalente. A Figura 9.5 mostra a substituição de 2 capacitores conectados em série por um equivalente.

Em geral, a ordem da equação diferencial n é igual a: n=n lc -n ce -n lj, onde n lc é o número de elementos reativos (L e C) no circuito, n ce é o número de elementos capacitivos circuitos, n lj é o número de nós ou seções indutivas.

Por capacitivo entende-se um circuito que consiste em elementos capacitivos ou elementos capacitivos e fontes de fem ideais. Fig. 9.6.a Por indutivo entende-se um nó para o qual convergem ramificações indutivas ou ramificações indutivas e fontes de corrente (Fig. 9.6.b), ou. seções que apenas cruzam ramos indutivos ou ramos indutivos e fontes de corrente.

Observe que a etapa de elaboração de uma equação diferencial não é obrigatória e a corrente ou tensão de transição pode ser encontrada sem a elaboração de uma equação. Como foi indicado, no método clássico de cálculo de processos transitórios resolvendo as equações é representado como a soma das soluções gerais e particulares.

Uma solução particular descreve um regime denominado forçado. A solução de uma equação homogênea (o lado direito é zero) descreve o processo na ausência de EMF externos e fontes de corrente e é chamada de livre. Correntes, tensões e cargas livres e forçadas são consideradas adequadamente.

Assim, a corrente no ramal com número K é representada como uma soma.

Definição. A equação característica de um operador linear f é uma equação da forma , onde λ é qualquer número real, A é a matriz do operador linear, E é a matriz identidade da mesma ordem.

Polinomial chamado polinômio característico matriz A (operador linear f). Na forma matricial, a equação característica tem a seguinte forma:

ou

.

Consequentemente, igualando o polinômio característico a zero, obtemos uma equação de grau sim, onde λ é a incógnita, obtemos os valores de suas raízes - os números característicos desta matriz. As raízes características desempenham um papel importante em muitas áreas da matemática. Consideremos uma das aplicações das raízes características - uma ferramenta muito importante no estudo de espaços lineares, bem como na resolução de muitos problemas aplicados de álgebra linear.

O conjunto de todas as raízes da equação característica é chamado de espectro do operador f(cada raiz é considerada com a multiplicidade que possui na equação característica).

Exemplo. Encontre as raízes características da matriz.

Vamos criar uma matriz

Igualando o polinômio característico a zero, obtemos uma equação quadrática

Então as raízes da equação são iguais .

Definição. Seja f um operador linear de espaço e seja algum vetor diferente de zero para o qual a igualdade

onde é um número real. Então o vetor é chamado de autovetor do operador e a matriz de seu operador, o autovalor ou autovalor da transformação. Neste caso, diz-se que o autovetor se refere ao autovalor.

Os autovetores desempenham um papel importante tanto na própria matemática quanto em suas aplicações. Por exemplo, ressonância, em que as frequências naturais de vibração do sistema coincidem com a frequência de vibração das forças externas. Em matemática, os autovetores são úteis na resolução de sistemas de equações diferenciais.

Teorema. Se um operador linear f tem a matriz A em sua base (primeira base) e a matriz B em sua base (segunda base), então a igualdade é válida: .

Conseqüentemente, ao passar para uma nova base, o polinômio característico do operador linear não muda.

◌ Se T é a matriz de transição da primeira base para a segunda, então. Então transformamos o lado direito da igualdade ●

Teorema. Para que o número λ 0 do corpo P seja um autovalor do vetor do espaço L n sobre P, é necessário e suficiente que o número λ 0 seja a raiz característica do operador f.

Doutor. EU. Necessidade. Deixar λ 0 autovalor do operador f, então em Ln existe um autovetor tal que.

Deixar é sua linha de coordenadas em alguma base, então

Por outro lado, porque , onde está a matriz de um operador linear em uma determinada base, então

Igualando os lados direitos de (1) e (2), obtemos:

(3)

Igualdades (3) significam que um vetor numérico com coordenadas é uma solução para o seguinte sistema de equações (4).

(4)

O vetor é diferente de zero (pois é próprio), portanto o sistema (4) tem solução diferente de zero, portanto seu determinante é 0.

(5)

e, portanto, o determinante transponível é igual a 0.

(6)

Se o diagrama de circuito contém capacitores conectados em paralelo C1, C2,... ou bobinas conectadas em série L1, L2,..., então, ao calcular processos transitórios, eles devem ser substituídos por um elemento equivalente SE = C1 + C2+... ou LE = L1 + L2+... λ 0 – raiz da equação característica.

II. Adequação. Deixar λ 0 – raiz característica do operador em alguma base . Vamos provar isso λ 0 é o autovalor do operador A.

Na verdade, se λ 0 é a raiz característica, então a igualdade (6) será satisfeita e, portanto, a igualdade (5), e isso significará que o sistema (4) tem soluções diferentes de zero.

Vamos escolher alguma solução diferente de zero do sistema (4): um vetor numérico . Então as igualdades (3) são satisfeitas.

Vamos considerar o vetor, e para ele a igualdade (2) será satisfeita e, em virtude da fórmula, a igualdade (1) é válida, onde está a matriz do operador na base EM. Isso implica a igualdade, o que significa que o vetor é um autovetor do operador ao qual o autovalor corresponde λ 0 . Era isso que precisava ser comprovado. O teorema foi provado.

Comentário. Para encontrar os autovalores do operador, é necessário compor e resolver a equação (5). Para encontrar os autovetores do operador, é necessário criar um sistema de equações (4) e encontrar um conjunto fundamental de soluções para este sistema.

Para controlar a exatidão do cálculo dos autovalores (podem ser coincidentes ou complexos), são utilizados dois fatos:

1) , onde a última soma da matriz traço é a soma dos elementos diagonais.

2) .

Exemplo. Encontre autovalores e autovetores .

Igualando a zero obtemos. .

3) . , .

Seja uma variável livre, então obtemos um vetor .

Exercício. Verifique o vetor.

.