Funções infinitamente grandes são suas propriedades. Definição de uma função infinitamente grande. Funções infinitesimais

A definição de uma sequência infinitamente grande é fornecida. São considerados os conceitos de vizinhança de pontos infinitamente distantes. É fornecida uma definição universal do limite de sequência, que se aplica tanto aos limites finitos quanto aos infinitos. São considerados exemplos de aplicação da definição de uma sequência infinitamente grande.

Contente

Veja também: Determinando o Limite de uma Sequência

Definição

Subsequência (β n) chamada de sequência infinitamente grande se para algum, número M arbitrariamente grande, existe tal número natural N M dependendo de M tal que para todos os números naturais n> N M a desigualdade
| β n | > M.
Neste caso, escreva
.
Ou em.
Eles dizem que tende ao infinito, ou converge para o infinito.

Se, a partir de algum número N 0 , então
( converge para mais infinito).
Se então
( converge para menos infinito).

Vamos escrever essas definições usando símbolos lógicos de existência e universalidade:
(1) .
(2) .
(3) .

As sequências com limites (2) e (3) são casos especiais de uma sequência infinitamente grande (1). Conclui-se dessas definições que se o limite de uma sequência é mais ou menos infinito, então também é igual ao infinito:
.
O inverso naturalmente não é verdade. Os membros da sequência podem ter caracteres alternados. Nesse caso, o limite pode ser igual ao infinito, mas sem um sinal definido.

Observe também que se alguma propriedade vale para uma sequência arbitrária com um limite igual ao infinito, então a mesma propriedade vale para uma sequência cujo limite é mais ou menos infinito.

Em muitos livros de análise matemática, a definição de uma sequência infinitamente grande indica que o número M é positivo: M > 0 ... No entanto, esse requisito é supérfluo. Se você cancelar, nenhuma contradição surgirá. Valores pequenos ou negativos não nos interessam. Estamos interessados ​​no comportamento da sequência para valores positivos arbitrariamente grandes de M. Portanto, se houver necessidade, então M pode ser limitado a partir de baixo por qualquer número predeterminado a, ou seja, podemos supor que M> a.

Quando determinamos ε - uma vizinhança do ponto final, então o requisito ε > 0 é importante. Com valores negativos, a desigualdade não pode ser satisfeita de forma alguma.

Bairros de pontos infinitamente distantes

Quando consideramos os limites finitos, introduzimos o conceito de vizinhança de um ponto. Lembre-se de que a vizinhança do ponto final é um intervalo aberto que contém esse ponto. Também podemos introduzir o conceito de vizinhança de pontos infinitamente distantes.

Seja M um número arbitrário.
Perto do ponto "infinito",, é chamado de conjunto.
Em torno do ponto "mais infinito",, é chamado de conjunto.
A vizinhança do ponto "menos infinito",, é chamado de conjunto.

A rigor, a vizinhança do ponto "infinito" é o conjunto
(4) ,
onde M 1 e M 2 - números positivos arbitrários. Usaremos a primeira definição porque é mais simples. No entanto, tudo o que é dito abaixo também é verdadeiro quando se usa a definição (4).

Podemos agora dar uma definição unificada de um limite de sequência que se aplica a limites finitos e infinitos.

Definição universal do limite de sequência.
Um ponto a (finito ou infinito) é o limite de uma sequência se para qualquer vizinhança deste ponto houver um número natural N tal que todos os elementos da sequência com números pertencem a esta vizinhança.

Assim, se o limite existe, então apenas um número finito de membros da sequência, ou um conjunto vazio, pode estar fora da vizinhança do ponto a. Essa condição é necessária e suficiente. A prova dessa propriedade é exatamente a mesma que para limites finitos.

Propriedade de vizinhança de uma sequência convergente
Para que o ponto a (finito ou infinitamente distante) seja o limite de uma sequência, é necessário e suficiente que fora de qualquer vizinhança desse ponto haja um número finito de membros da sequência ou um conjunto vazio.
Prova .

Além disso, às vezes o conceito de ε - vizinhanças de pontos infinitamente distantes é introduzido.
Lembre-se de que ε - uma vizinhança do ponto final a é chamada de conjunto.
Introduzir próxima designação... Seja ε uma vizinhança do ponto a. Então, para o ponto final,
.
Para pontos no infinito:
;
;
.
Usando o conceito de ε - vizinhanças, pode-se dar mais uma definição universal do limite de uma sequência:

O ponto a (ponto final ou no infinito) é o limite da sequência se for algum número positivo ε > 0 existe um número natural N ε dependendo de ε tal que para todos os números n> N ε os termos x n pertencem à ε - vizinhança do ponto a:
.

Usando os símbolos lógicos de existência e universalidade, esta definição será escrita da seguinte forma:
.

Exemplos de sequências infinitamente grandes

Exemplo 1

.

.
Vamos escrever a definição de uma sequência infinitamente grande:
(1) .
No nosso caso
.

Nós introduzimos números e, conectando-os com desigualdades:
.
Pelas propriedades das desigualdades, se e, então
.
Observe que, pois, essa desigualdade vale para qualquer n. Portanto, você pode escolher desta forma:
no ;
no .

Portanto, para qualquer um, pode-se encontrar um número natural que satisfaça a desigualdade. Então, para todos,
.
Significa que . Ou seja, a sequência é infinitamente grande.

Exemplo 2

Usando a definição de uma sequência infinitamente grande, mostre que
.

(2) .
O termo geral da sequência dada tem a forma:
.

Insira números e:
.
.

Então, para qualquer um pode encontrar um número natural que satisfaça a desigualdade, de modo que, para todos,
.
Significa que .

.

Exemplo 3

Usando a definição de uma sequência infinitamente grande, mostre que
.

Vamos escrever a definição do limite de uma sequência igual a menos infinito:
(3) .
O termo geral da sequência dada tem a forma:
.

Insira números e:
.
Isso mostra que se você, então
.

Uma vez que para qualquer um pode encontrar um número natural que satisfaça a desigualdade, então
.

Para um dado, como N, pode-se tomar qualquer número natural que satisfaça a seguinte desigualdade:
.

Exemplo 4

Usando a definição de uma sequência infinitamente grande, mostre que
.

Vamos escrever o termo geral da sequência:
.
Vamos escrever a definição do limite de sequência igual a mais infinito:
(2) .

Como n é um número natural, n = 1, 2, 3, ... , então
;
;
.

Introduzimos números e M, conectando-os por desigualdades:
.
Isso mostra que se você, então
.

Portanto, para qualquer número M, pode-se encontrar um número natural que satisfaça a desigualdade. Então, para todos,
.
Significa que .

Referências:
L. D. Kudryavtsev. O curso da análise matemática. Volume 1. Moscou, 2003.
CM. Nikolsky. O curso da análise matemática. Volume 1. Moscou, 1983.

Veja também:

Função y = f (x) chamado infinitesimal no x → a ou em x→ ∞ se ou, ou seja, infinitamente pequena funçãoÉ uma função cujo limite em um determinado ponto é zero.

Exemplos.

1. Função f (x)=(x-1) 2 é infinitesimal para x→ 1, desde (ver fig.).

2. Função f (x)= tg x- infinitamente pequeno em x→0.

3. f (x)= ln (1+ x) É infinitamente pequeno para x→0.

4. f (x) = 1/x- infinitamente pequeno em x→∞.

Vamos estabelecer a seguinte relação importante:

Teorema. Se a função y = f (x) representável em x → a como a soma de um número constante b e valor infinitesimal α (x): f (x) = b + α (x) então .

Por outro lado, se, então f (x) = b + α (x), Onde a (x)- infinitamente pequeno em x → a.

Prova.

1. Vamos provar a primeira parte da afirmação. De igualdade f (x) = b + α (x) deve | f (x) - b | = | α |... Mas desde a (x)É infinitamente pequeno, então para ε arbitrário há δ - uma vizinhança do ponto uma, com tudo x a partir da qual, os valores a (x) satisfazer a relação | α (x) |< ε. Então | f (x) - b |< ε. E isso significa isso.

2. Se, então para qualquer ε >0 para todos NS de algum δ é uma vizinhança do ponto uma vai | f (x) - b |< ε. Mas se denotarmos f (x) - b = α, então | α (x) |< ε, o que significa que uma- infinitamente pequeno.

Considere as propriedades básicas das funções infinitesimais.

Teorema 1. A soma algébrica de dois, três e, em geral, qualquer número finito de infinitesimal é uma função infinitesimal.

Prova... Deixe-nos dar uma prova para dois termos. Deixe ser f (x) = α (x) + β (x) onde e. Precisamos provar que para um ε arbitrariamente pequeno > 0 é encontrado δ> 0 tal que para x satisfazendo a desigualdade | x - a |<δ , realizado | f (x) |< ε.

Então, fixamos um número arbitrário ε > 0. Visto que pela hipótese do teorema α (x)É uma função infinitesimal, então existe δ 1 > 0, que para | x - a |< δ 1 nós temos | α (x) |< ε / 2. Da mesma forma, desde β (x)É infinitamente pequeno, então há δ 2 > 0, que para | x - a |< δ 2 nós temos | β (x) |< ε / 2.

Vamos levar δ = min (δ 1 , δ 2 } . Então, nas proximidades do ponto uma raio δ cada uma das desigualdades | α (x) |< ε / 2 e | β (x) |< ε / 2. Portanto, neste bairro haverá

| f (x) | = | α (x) + β (x)| ≤ | α (x) | + | β (x) |< ε /2 + ε /2= ε,

Essa. | f (x) |< ε, conforme necessário.

Teorema 2. Produto de uma função infinitesimal a (x) para função limitada f (x) no x → a(ou em x → ∞) é uma função infinitesimal.

Prova... Uma vez que a função f (x)é limitado, então há um número M de modo que para todos os valores x de algum bairro do ponto a | f (x) | ≤M. Além disso, desde a (x)É uma função infinitesimal em x → a, então para ε arbitrário > 0 há uma vizinhança do ponto uma, em que a desigualdade | α (x) |< ε / M... Então, no menor desses bairros, temos | αf |< ε / M= ε. E isso significa que af- infinitamente pequeno. Para a ocasião x → ∞ a prova é semelhante.

O teorema provado implica:

Corolário 1. Se e, então.

Corolário 2. Se c = const, então.

Teorema 3. Taxa de função infinitesimal α (x) por função f (x), cujo limite é diferente de zero, é uma função infinitesimal.

Prova... Deixe ser . Então 1 / f (x) existe uma função limitada. Portanto, a fração é o produto de uma função infinitesimal e uma função limitada, ou seja, função é infinitesimal.

Cálculo do infinitesimal e grande

Cálculo infinitesimal- cálculos realizados com valores infinitesimais, nos quais o resultado derivado é considerado uma soma infinita de valores infinitesimais. O cálculo de quantidades infinitesimais é um conceito geral para cálculo diferencial e integral, que forma a base da matemática superior moderna. O conceito de quantidade infinitesimal está intimamente relacionado ao conceito de limite.

Infinitamente pequeno

Subsequência uma n chamado infinitesimal, E se . Por exemplo, uma sequência de números é infinitesimal.

A função é chamada infinitesimal na vizinhança do ponto x 0 se .

A função é chamada infinitesimal no infinito, E se ou .

Também infinitesimal é uma função que é a diferença entre uma função e seu limite, ou seja, se , então f(x) − uma = α( x) , .

Valor infinitamente grande

Subsequência uma n chamado infinitamente grande, E se .

A função é chamada infinitamente grande na vizinhança do ponto x 0 se .

A função é chamada infinitamente grande no infinito, E se ou .

Em todos os casos, o infinito à direita da igualdade implica um certo sinal ("mais" ou "menos"). Essa é, por exemplo, a função x pecado x não é infinitamente grande.

Propriedades de infinitesimal e infinitamente grande

Comparação de quantidades infinitesimais

Como você compara valores infinitesimais?
A proporção de quantidades infinitesimais forma a chamada incerteza.

Definições

Suponha que temos infinitesimal para o mesmo valor α ( x) e β ( x) (ou, o que não é importante para a definição, sequências infinitesimais).

É conveniente usar a regra de L'Hôpital para calcular esses limites.

Exemplos de comparação

Usando O-símbolos, os resultados obtidos podem ser escritos da seguinte forma x 5 = o(x 3). Neste caso, as seguintes entradas são válidas 2x 2 + 6x = O(x) e x = O(2x 2 + 6x).

Quantidades equivalentes

Definição

Se, então, as quantidades infinitesimais α e β são chamadas equivalente ().
Obviamente, quantidades equivalentes são um caso especial de quantidades infinitesimais da mesma ordem de pequenez.

Pois, as seguintes relações de equivalência são válidas: ,, .

Teorema

O limite do quociente (razão) de duas quantidades infinitesimais não muda se uma delas (ou ambas) for substituída por uma quantidade equivalente.

Este teorema é de importância prática para encontrar os limites (veja o exemplo).

Exemplo de uso

Substituindo seun 2x valor equivalente 2 x, Nós temos

Esboço histórico

O conceito de "infinitesimal" foi discutido nos tempos antigos em conexão com o conceito de átomos indivisíveis, mas não entrou na matemática clássica. Ele foi revivido novamente com o surgimento no século 16 do “método dos indivisíveis” - dividindo a figura em estudo em seções infinitamente pequenas.

No século 17, ocorreu a algebraização do cálculo infinitesimal. Eles começaram a ser definidos como valores numéricos que são menores que qualquer valor finito (diferente de zero) e ainda não são iguais a zero. A arte da análise consistia em traçar uma relação contendo infinitesimais (diferenciais) e, em seguida, integrá-la.

Os matemáticos da velha escola expuseram o conceito infinitesimal crítica severa. Michel Roll escreveu que o novo cálculo é “ um conjunto de erros engenhosos"; Voltaire observou sarcasticamente que esse cálculo é a arte de calcular e medir coisas com precisão, cuja existência não pode ser provada. Até Huygens admitiu que não entendia o significado dos diferenciais de ordem superior.

Como ironia do destino, pode-se considerar o surgimento, em meados do século, da análise atípica, que provou que o ponto de vista original - o infinitesimal real - também é consistente e poderia ser usado como base para a análise.

Veja também

Fundação Wikimedia. 2010.

Veja o que é "Infinitamente grande" em outros dicionários:

Variável Y, o recíproco do valor infinitesimal X, ou seja, Y = 1 / X ... Grande Dicionário Enciclopédico

Variável y, o recíproco do valor infinitesimal x, ou seja, y = 1 / x. * * * INFINITAMENTE GRANDE INFINITAMENTE GRANDE, variável Y, inverso do infinitesimal X, ou seja, Y = 1 / X ... dicionário enciclopédico

Em matemática, uma variável que em um determinado processo de mudança torna-se e permanece em valor absoluto maior que qualquer número predeterminado. Estudo de B.. as quantidades podem ser reduzidas ao estudo do infinitesimal (Ver ... ... Grande Enciclopédia Soviética

INFINITAS PEQUENAS FUNÇÕES E SUAS PROPRIEDADES BÁSICAS

Função y = f (x) chamado infinitesimal no x → a ou em x→ ∞ se ou, ou seja, uma função infinitesimal é uma função cujo limite em um determinado ponto é zero.

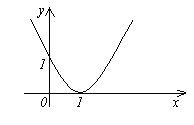
Exemplos.

Vamos estabelecer a seguinte relação importante:

Teorema. Se a função y = f (x) representável em x → a como a soma de um número constante b e valor infinitesimal α (x): f (x) = b + α (x) então .

Por outro lado, se, então f (x) = b + α (x), Onde a (x)- infinitamente pequeno em x → a.

Prova.

Considere as propriedades básicas das funções infinitesimais.

Teorema 1. A soma algébrica de dois, três e, em geral, qualquer número finito de infinitesimal é uma função infinitesimal.

Prova... Deixe-nos dar uma prova para dois termos. Deixe ser f (x) = α (x) + β (x) onde e. Precisamos provar que para um ε arbitrariamente pequeno > 0 é encontrado δ> 0 tal que para x satisfazendo a desigualdade | x - a |<δ , realizado | f (x) |< ε.

Então, fixamos um número arbitrário ε > 0. Visto que pela hipótese do teorema α (x)É uma função infinitesimal, então existe δ 1 > 0, que para | x - a |< δ 1 nós temos | α (x) |< ε / 2. Da mesma forma, desde β (x)É infinitamente pequeno, então há δ 2 > 0, que para | x - a |< δ 2 nós temos | β (x) |< ε / 2.

Vamos levar δ = min (δ 1 , δ 2 } . Então, nas proximidades do ponto uma raio δ cada uma das desigualdades será satisfeita | α (x) |< ε / 2 e | β (x) |< ε / 2. Portanto, neste bairro haverá

| f (x) | = | α (x) + β (x)| ≤ | α (x) | + | β (x) |< ε /2 + ε /2= ε,

Essa. | f (x) |< ε, conforme necessário.

Teorema 2. Produto de uma função infinitesimal a (x) para função limitada f (x) no x → a(ou em x → ∞) é uma função infinitesimal.

Prova... Uma vez que a função f (x)é limitado, então há um número M de modo que para todos os valores x de algum bairro do ponto a | f (x) | ≤M. Além disso, desde a (x)É uma função infinitesimal em x → a, então para ε arbitrário > 0 há uma vizinhança do ponto uma, em que a desigualdade | α (x) |< ε / M... Então, no menor desses bairros, temos | αf |< ε / M= ε. E isso significa que af- infinitamente pequeno. Para a ocasião x → ∞ a prova é semelhante.

O teorema provado implica:

Corolário 1. Se e, então.

Corolário 2. Se c = const, então.

Teorema 3. Taxa de função infinitesimal α (x) por função f (x), cujo limite é diferente de zero, é uma função infinitesimal.

Prova... Deixe ser ... Então 1 / f (x) existe uma função limitada. Portanto, a fração é o produto de uma função infinitesimal por uma função limitada, ou seja, função é infinitesimal.

RELAÇÃO ENTRE FUNÇÕES INFINITAS PEQUENAS E INFINITAMENTE GRANDES

Teorema 1. Se a função f (x)é infinitamente grande para x → a, então a função 1 / f (x)é infinitesimal para x → a.

Prova. Pegue um número arbitrário ε >0 e mostrar isso para alguns δ>0 (dependendo de ε) para todos x para qual | x - a |<δ , a desigualdade se mantém, e isso significa que 1 / f (x)É uma função infinitesimal. Na verdade, desde f (x)É uma função infinitamente grande em x → a, então há δ>0 tal que assim que | x - a |<δ então | f (x) |> 1/ ε. Mas então pelo mesmo x.

Exemplos.

O teorema inverso também pode ser provado.

Teorema 2. Se a função f (x)- infinitamente pequeno em x → a(ou x → ∞) e não desaparece, então y = 1/ f (x)é uma função infinitamente grande.

Prove o teorema você mesmo.

Exemplos.

Assim, as propriedades mais simples de funções infinitesimais e infinitamente grandes podem ser escritas usando as seguintes relações condicionais: UMA≠ 0

LIMIT THEORES

Teorema 1. O limite da soma algébrica de dois, três e geralmente um certo número de funções é igual à soma algébrica dos limites dessas funções, ou seja,

Prova... Façamos a prova para dois termos, visto que é feita da mesma maneira para qualquer número de termos. Deixe ser .Então f (x) = b + α (x) e g (x) = c + β (x), Onde α e β - funções infinitesimais. Portanto,

f (x) + g (x) = (b + c) + (α (x) + β (x)).

Porque b + cé uma constante, e α (x) + β (x)- a função é infinitesimal, então

Exemplo. ...

Teorema 2. O limite do produto de dois, três e geralmente um número finito de funções é igual ao produto dos limites dessas funções:

Prova... Deixe ser ... Portanto, f (x) = b + α (x) e g (x) = c + β (x) e

fg = (b + α) (c + β) = bc + (bβ + cα + αβ).

Trabalhar ac existe um valor constante. Função bβ + c α + αβ com base nas propriedades das funções infinitesimais, existe uma quantidade infinitamente pequena. É por isso .

Corolário 1. O fator constante pode ser retirado do sinal de limite:

.

Corolário 2. Limite de grau igual ao grau limite:

.

Exemplo..

Teorema 3. O limite de quociente de duas funções é igual ao quociente dos limites dessas funções se o limite do denominador for diferente de zero, ou seja,

.

Prova... Deixe ser . Portanto, f (x) = b + α (x) e g (x) = c + β (x), Onde α, β - infinitamente pequeno. Considere o privado

A fração é uma função infinitesimal, visto que o numerador é uma função infinitesimal, e o denominador tem um limite c 2 ≠ 0.

Exemplos.

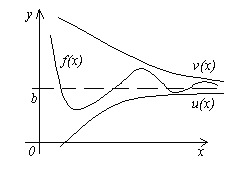
Teorema 4. Dadas três funções f (x), u (x) e v (x) satisfazendo as desigualdades u (x) ≤f (x) ≤ v (x)... Funções If u (x) e v (x) tem o mesmo limite em x → a(ou x → ∞), então a função f (x) tende para o mesmo limite, ou seja, E se

, então .

O significado deste teorema é claro na figura.

A prova do Teorema 4 pode ser encontrada, por exemplo, no livro didático: Piskunov N.S. Differential and integral calculus, vol. 1 - Moscou: Nauka, 1985.

Teorema 5. Se em x → a(ou x → ∞) função y = f (x) assume valores não negativos y≥0 e ao mesmo tempo tende ao limite b, então este limite não pode ser negativo: b≥0.

Prova... Realizamos a prova por contradição. Vamos fingir que b<0 , então | y - b | ≥ | b | e, portanto, o módulo da diferença não tende a zero como x → a... Mas então y não tende ao limite b no x → a, o que contradiz a hipótese do teorema.

Teorema 6. Se duas funções f (x) e g (x) para todos os valores do argumento x satisfazer a desigualdade f (x) ≥ g (x) e tem limites, então a desigualdade b≥c.

Prova. Pela hipótese do teorema f (x) -g (x) ≥0, portanto, pelo Teorema 5 , ou .

LIMITES DE UM LADO

Até agora, consideramos a definição do limite de uma função quando x → a de forma arbitrária, ou seja, o limite da função não dependia de como o x para uma, à esquerda ou à direita de uma... No entanto, muitas vezes você pode encontrar funções que não têm um limite sob esta condição, mas eles têm um limite se x → a ficando de um lado de uma, esquerda ou direita (ver fig.). Portanto, o conceito de limites unilaterais é introduzido.

Se f (x) tende ao limite b no x atendendo a um certo número uma tão x leva apenas valores menores que uma, então eles escrevem e ligam b pelo limite da função f (x) no ponto a à esquerda.

Cálculo do infinitesimal e grande

Cálculo infinitesimal- cálculos realizados com valores infinitesimais, nos quais o resultado derivado é considerado uma soma infinita de valores infinitesimais. O cálculo de quantidades infinitesimais é um conceito geral para cálculo diferencial e integral, que forma a base da matemática superior moderna. O conceito de quantidade infinitesimal está intimamente relacionado ao conceito de limite.

Infinitamente pequeno

Subsequência uma n chamado infinitesimal, E se . Por exemplo, uma sequência de números é infinitesimal.

A função é chamada infinitesimal na vizinhança do ponto x 0 se .

A função é chamada infinitesimal no infinito, E se ou .

Também infinitesimal é uma função que é a diferença entre uma função e seu limite, ou seja, se , então f(x) − uma = α( x) , .

Valor infinitamente grande

Em todas as fórmulas abaixo, infinito à direita da igualdade implica um certo sinal ("mais" ou "menos"). Essa é, por exemplo, a função x pecado x, ilimitado em ambos os lados, não é infinitamente grande em.

Subsequência uma n chamado infinitamente grande, E se .

A função é chamada infinitamente grande na vizinhança do ponto x 0 se .

A função é chamada infinitamente grande no infinito, E se ou .

Propriedades de infinitesimal e infinitamente grande

Comparação de quantidades infinitesimais

Como você compara valores infinitesimais?
A proporção de quantidades infinitesimais forma a chamada incerteza.

Definições

Suponha que temos infinitesimal para o mesmo valor α ( x) e β ( x) (ou, o que não é importante para a definição, sequências infinitesimais).

É conveniente usar a regra de L'Hôpital para calcular esses limites.

Exemplos de comparação

Usando O-símbolos, os resultados obtidos podem ser escritos da seguinte forma x 5 = o(x 3). Neste caso, as seguintes entradas são válidas 2x 2 + 6x = O(x) e x = O(2x 2 + 6x).

Quantidades equivalentes

Definição

Se, então, as quantidades infinitesimais α e β são chamadas equivalente ().
Obviamente, quantidades equivalentes são um caso especial de quantidades infinitesimais da mesma ordem de pequenez.

Pois, as seguintes relações de equivalência são válidas (como consequência dos chamados limites notáveis):

Teorema

O limite do quociente (razão) de duas quantidades infinitesimais não muda se uma delas (ou ambas) for substituída por uma quantidade equivalente.

Este teorema é de importância prática para encontrar os limites (veja o exemplo).

Exemplo de uso

Substituindo seun 2x valor equivalente 2 x, Nós temos

Esboço histórico

O conceito de "infinitesimal" foi discutido nos tempos antigos em conexão com o conceito de átomos indivisíveis, mas não entrou na matemática clássica. Ele foi revivido novamente com o surgimento no século 16 do “método dos indivisíveis” - dividindo a figura em estudo em seções infinitamente pequenas.

No século 17, ocorreu a algebraização do cálculo infinitesimal. Eles começaram a ser definidos como valores numéricos que são menores que qualquer valor finito (diferente de zero) e ainda não são iguais a zero. A arte da análise consistia em traçar uma relação contendo infinitesimais (diferenciais) e, em seguida, integrá-la.

Os matemáticos da velha escola expuseram o conceito infinitesimal crítica severa. Michel Roll escreveu que o novo cálculo é “ um conjunto de erros engenhosos"; Voltaire observou sarcasticamente que esse cálculo é a arte de calcular e medir coisas com precisão, cuja existência não pode ser provada. Até Huygens admitiu que não entendia o significado dos diferenciais de ordem superior.

Como ironia do destino, pode-se considerar o surgimento, em meados do século, da análise atípica, que provou que o ponto de vista original - o infinitesimal real - também é consistente e poderia ser usado como base para a análise.

Veja também

Fundação Wikimedia. 2010.

Veja o que é "valor infinitamente pequeno" em outros dicionários:

VALOR INFINITO PEQUENO- um valor variável em um determinado processo, se neste processo se aproxima infinitamente (tende) a zero ... Big Polytechnic Encyclopedia

Quantidade infinitamente pequena- ■ Algo desconhecido, mas relacionado à homeopatia ... Léxico de verdades comuns