Funkcje wektorowe historii pojawiania się argumentów skalarnych. Określanie funkcji przy użyciu wektora prawdy. Określanie użycia pełnego drzewa binarnego

i jego zróżnicowanie.

Jednym z najprostszych sposobów określenia krzywej przestrzennej jest określenie równania wektorowego:

Gdzie jest wektorem promienia punktu krzywej, oraz - parametr określający położenie punktu.

To. wektor zmienny istnieje funkcja skalarna . W analizie matematycznej takie funkcje nazywane są funkcjami wektorowymi argumentu skalarnego.

Rozkład stosując wektory jednostkowe, równanie (1) można zapisać w postaci:

To rozwinięcie pozwala przejść do równania parametrycznego krzywej:

Innymi słowy, określenie funkcji wektorowej jest równoznaczne z określeniem trzech funkcji skalarnych.

W odniesieniu do funkcji wektorowej (1) definiującej tę krzywą, sama krzywa nazywana jest hodografem tej funkcji. Początek współrzędnych nazywany jest w tym przypadku biegunem hodografu.

Niech to teraz
I
- punkty krzywej określone równaniem (1). Ponadto
, A
Wektory promieni tych punktów będą wynosić

I
.

Wektor
nazywany przyrostem funkcji wektorowej
, odpowiadający przyrostowi
jego argument i jest oznaczony przez
,

Funkcja wektorowa
będzie funkcją ciągłą , Jeśli

.

Aby znaleźć pochodną
postępujmy następująco -

.

Ustalmy teraz kierunek
. To oczywiste współliniowy z
i o godz
skierowany w tym samym kierunku co
i kiedy
- w przeciwnym kierunku. Ale w pierwszym przypadku
i w drugim
To. wektor zawsze skierowane wzdłuż siecznego hodografu
w górę .

Jeśli użyjemy rozwinięcia I w takim razie przez orty

Stąd dzieląc (*) przez
i dochodzimy do granic
Dla
dostajemy

Na podstawie (4) można wykazać, że obowiązują następujące wzory:

(5)

(6)

- funkcja skalarna.

Dowód (7).

Przeanalizujmy teraz niektóre właściwości
. Na początek znajdźmy jego moduł:

.

Ponieważ uważamy zatem, że łuk hodografu jest możliwy do naprawienia
- jest długością cięciwy, i
- długość łuku. Dlatego

To. moduł pochodnej funkcji wektorowej argumentu skalarnego jest równy pochodnej łuku hodografu względem tego samego argumentu.

Wniosek 1. Jeśli - wektor jednostkowy skierowany stycznie do hodografu w kierunku wzrostu , To

Wniosek 2. Jeśli jako argument funkcji wektorowej przyjmiemy długość łuku hodografu , To

(ponieważ
)

To. pochodna funkcji wektorowej po długości łuku hodografu jest równa wektorowi jednostkowemu stycznej do hodografu, skierowanej w stronę zwiększania długości łuku.

Wniosek 3. Jeśli hodograf funkcji wektorowej zostanie uznany za trajektorię punktu, i - jako czas ruchu, liczony od pewnego , To
pokrywa się pod względem wielkości i kierunku z wektorem prędkości ruchu
.

W rzeczywistości wartość skalarna prędkości jest równa pochodnej ścieżki po czasie:

Poza tym wektor skierowany stycznie do trajektorii w kierunku ruchu, który odpowiada kierunkowi wzrostu , tj. odpowiada kierunkowi .

To.
.

Rozważmy teraz
, którego długość jest stała,
, tj.

(*)
Gdzie

Różniczkując (*) znajdujemy:

Te.

W szczególności pochodna wektora dowolnej zmiennej w kierunku jednostki Zawsze
.

Niech to teraz
kąt między promieniami kuli jednostkowej poprowadzonymi do punktów
I
hodograf
. Następnie długość cięciwy
z trójkąta
będzie równe

Wielkość pochodnej jednostkowego wektora zmiennej jest równa prędkości kątowej obrotu tego wektora.

Jeśli chodzi o funkcje skalarne, różnicę funkcji wektorowej zapisuje się jako

Ale nawet wtedy

Krzywizna krzywej przestrzennej.

Towarzyszący trójścian.

Zgodnie z wnioskiem 2, dla możemy zapisać wzór:

Zmiana kierunku , związana ze zmianą stycznej do krzywej przestrzennej, charakteryzuje krzywiznę krzywej. Jako miarę krzywizny krzywej przestrzennej, podobnie jak krzywej płaskiej, przyjmuje się granicę stosunku kąta przylegania do długości łuku, gdy

krzywizna,
kąt przylegania,
długość łuku.

Po drugiej stronie
wektor jednostkowy i jego wektor pochodny jest do niego prostopadła oraz jego moduł
Różnicowanie Przez i wejście
wektor jednostkowy z kierunkiem , znajdujemy:

Wektor
wektor krzywizny krzywej przestrzennej. Jego kierunek, prostopadły do ​​kierunku stycznej, jest kierunkiem normalnym krzywej przestrzennej. Jednak krzywa przestrzenna ma w dowolnym punkcie nieskończoną liczbę normalnych, z których wszystkie leżą w płaszczyźnie przechodzącej przez dany punkt krzywej i prostopadłej do stycznej w danym punkcie. Płaszczyzna ta nazywana jest płaszczyzną normalną krzywej przestrzennej.

Definicja. Normalna krzywej, wzdłuż której wektor krzywizny krzywej jest skierowany w dany punkt, jest główną normalną krzywej przestrzennej. To.
główny wektor normalny jednostki.

Skonstruujmy teraz trzeci wektor jednostkowy równy iloczynowi krzyżowemu I

Wektor , tak jak również prostopadłe te. leży w płaszczyźnie normalnej. Jego kierunek nazywany jest kierunkiem binormalnej krzywej przestrzennej w danym punkcie. Wektor
I stanowią trio wzajemnie prostopadłych wektorów jednostkowych, których kierunek zależy od położenia punktu na krzywej przestrzennej i zmienia się w zależności od punktu. Wektory te tworzą tzw. towarzyszący trójścian (trójścian Freneta) krzywej przestrzennej. Wektor
I tworzą prawą trójkę, podobnie jak jednostkowe wektory jednostkowe
we właściwym układzie współrzędnych.

Brane w parach
zdefiniuj trzy płaszczyzny przechodzące przez ten sam punkt krzywej i tworzące ściany towarzyszącego trójścianu. Naraz I określić płaszczyznę oscylacji (łuk krzywej w sąsiedztwie danego punktu jest łukiem krzywej płaszczyzny w płaszczyźnie oscylacji z dokładnością wyższego rzędu);

I - płaszczyzna prostująca;

I - normalny samolot.

Równania styczne, normalne i binormalne.

Równania płaszczyzn towarzyszącego trójścianu.

Porozumiewawczy
I lub dowolne wektory niejednostkowe współliniowe z nimi T., N I B Wyprowadźmy równania wymienione w tej sekcji.

W tym celu w równanie kanoniczne bezpośredni

oraz w równaniu płaszczyzny przechodzącej przez dany punkt

wziąć za
współrzędne wybranego punktu na krzywej, np
lub odpowiednio dla
weź współrzędne wektorów
Lub
, który określa kierunek żądanej linii lub normalnej do żądanej płaszczyzny:

Lub - dla płaszczyzny stycznej lub normalnej,

Lub - dla głównej płaszczyzny normalnej i prostującej,

Lub - dla płaszczyzny binormalnej i oscylacyjnej.

Jeśli krzywa jest dana równaniem wektorowym
Lub
następnie dla wektora
można przyjąć skierowane stycznie

Aby znaleźć
I najpierw znajdźmy rozkład
przez wektory
Wcześniej (wniosek 1) znaleźliśmy to
Różnicowanie przez , otrzymujemy:

Ale, ponieważ

Pomnóżmy teraz wektorowo I

(*)

Na podstawie (*) na wektor , mając kierunek binormalny, moglibyśmy przyjąć wektor

Ale wtedy, dla
możemy wziąć iloczyn wektorowy tych ostatnich:

To. w dowolnym punkcie dowolnej krzywej możemy wyznaczyć wszystkie elementy towarzyszącego trójścianu.

Przykład. Równanie stycznej, normalnej i binormalnej do prawej helisy w dowolnym punkcie.

Tangens

Dom normalny

Binormalny

Niech zbiór wartości funkcji wektorowej argumentu skalarnego zostanie zredukowany do wspólnego początku w punkcie 0. Dopasujmy początek kartezjańskiego układu współrzędnych do tego punktu. Następnie dowolny wektor można rozwinąć na wektory jednostkowe

Zatem określenie funkcji wektorowej argumentu skalarnego oznacza określenie trzech funkcji skalarnych Kiedy wartość argumentu ulegnie zmianie, koniec wektora będzie opisywał krzywą w przestrzeni, co nazywa się hodografem wektorowym

Niech będzie bliska wartość dla Następnie wywoływana jest pochodna funkcji wektorowej do argumentu skalarnego

Nr 17 Prędkość i przyspieszenie punktu w ruchu krzywoliniowym

Prędkość

Prędkość jest wprowadzana jako cecha ruchu punktu materialnego. Prędkość jest wielkością wektorową, którą charakteryzuje zarówno prędkość ruchu (wielkość wektora prędkości), jak i jego kierunek (kierunek wektora prędkości) w w tej chwili czas. Pozwalać punkt materialny porusza się po krzywoliniowej trajektorii i w chwili t odpowiada wektorowi promienia r0 (rys. 1). W krótkim czasie Δt punkt przebędzie podróż Δs i jednocześnie doznaje elementarnego (nieskończenie małego) przemieszczenia Δr.

Wektor średniej prędkości nazywa się stosunkiem przyrostu Δr wektora promienia punktu do przedziału czasu Δt:

Kierunek wektora średniej prędkości pokrywa się z kierunkiem Δr. Przy nieskończonym spadku Δt średnia prędkość dąży do wartości zwanej prędkością chwilową v:

Oznacza to, że prędkość chwilowa v jest wielkością wektorową równą pierwszej pochodnej wektora promienia poruszającego się punktu po czasie. Ponieważ w granicy sieczna pokrywa się ze styczną, wówczas wektor prędkości v jest skierowany stycznie do trajektorii w kierunku ruchu (ryc. 2).

Ryc.2

Gdy Δt maleje, Δs będzie coraz bardziej zbliżać się do |Δr|, zatem moduł prędkości chwilowej

Oznacza to, że wartość bezwzględna prędkości chwilowej jest równa pierwszej pochodnej drogi po czasie:

Przy nierównym ruchu moduł prędkości chwilowej jest inny w różnych momentach. W takim przypadku użyj wielkości skalarnej - średnia prędkość ruchu nierównego:

Jeśli scałkujemy wyrażenie ds=vdt w czasie w zakresie od t do t+Δt (patrz wzór (2)), znajdziemy długość drogi przebytej przez punkt w czasie Δt:

W przypadku ruchu jednostajnego wartość liczbowa prędkości chwilowej jest stała; Wtedy wyrażenie (3) przyjmie postać

Długość drogi przebytej przez punkt w czasie od t1 do t2 jest wyrażona całką

PRZYŚPIESZENIE

Podczas nierównej jazdy często konieczna jest wiedza o tym, jak szybko zmienia się prędkość w czasie. Wielkość fizyczna charakteryzująca szybkość zmiany prędkości pod względem wielkości i kierunku nazywana jest przyspieszeniem. Rozważmy ruch płaski - ruch, w którym trajektorie każdego punktu rozpatrywanego układu leżą w tej samej płaszczyźnie. Niech wektor v będzie prędkością punktu A w chwili t. W czasie Δt punkt przemieścił się do pozycji B i otrzymał prędkość różną od v zarówno co do wartości, jak i kierunku, i równą v1 + Δv. Przesuńmy wektor v1 do punktu A i znajdźmy Δv (rys. 1).

Średnie przyspieszenie ruchu nierównomiernego w przedziale od t do t+Δt jest wielkością wektorową równą stosunkowi zmiany prędkości Δv do przedziału czasu Δt:

Chwilowe przyspieszenie a (przyspieszenie) punktu materialnego w chwili t będzie wielkością wektorową:

równa pierwszej pochodnej prędkości po czasie.

Rozłóżmy wektor Δv na dwie składowe. W tym celu z punktu A (rys. 1) w kierunku prędkości v wykreślamy wektor AD, którego moduł jest równy v1. Oczywiście wektor CD równy Δvτ wyznacza zmianę prędkości w czasie Δt modulo: Δvτ=v1-v. Druga składowa Δvn wektora Δv charakteryzuje zmianę prędkości w czasie Δt w kierunku.

Styczna składowa przyspieszenia:

tj. jest równa pierwszej pochodnej po czasie modułu prędkości, określając w ten sposób szybkość zmiany modułu prędkości.

Szukamy drugiej składowej przyspieszenia. Zakładamy, że punkt B leży bardzo blisko punktu A, zatem Δs można uznać za łuk okręgu o promieniu r, nieznacznie różniącym się od cięciwy AB. Trójkąt AOB jest podobny do trójkąta EAD, z którego wynika Δvn/AB=v1/r, ale skoro AB=vΔt, to

W granicy w Δt → 0 otrzymujemy v1 → v.

Ponieważ v1 → v, kąt EAD dąży do zera, a ponieważ trójkąt EAD jest równoramienny, wówczas kąt ADE pomiędzy v i Δvn ma tendencję do kąta prostego. W rezultacie w Δt → 0 wektory Δvn i v stają się wzajemnie prostopadłe. Ponieważ wektor prędkości jest skierowany stycznie do trajektorii, następnie wektor Δvn, prostopadły do ​​wektora prędkości, jest skierowany do środka krzywizny trajektorii punktu. Drugi składnik przyspieszenia, równy

nazywa się składową normalną przyspieszenia i jest skierowany wzdłuż linii prostej prostopadłej do stycznej do trajektorii (zwanej normalną) do środka jej krzywizny (dlatego nazywa się ją również przyspieszeniem dośrodkowym).

Pełne przyspieszenie ciało jest sumą geometryczną składowych stycznych i normalnych (ryc. 2):

Oznacza to, że składowa styczna przyspieszenia jest cechą szybkości zmiany prędkości pod względem wielkości (skierowaną stycznie do trajektorii), a składowa normalna przyspieszenia jest charakterystyką szybkości zmiany prędkości w kierunku (skierowanym w kierunku środek krzywizny trajektorii). W zależności od składowej stycznej i normalnej przyspieszenia, ruch można sklasyfikować w następujący sposób:

1)aτ=0, an=0 - prostoliniowy ruch jednostajny;

2)aτ=an=const, аn=0 - prostoliniowy ruch jednostajny. Z tego typu ruchem

Jeżeli czas początkowy t1 = 0 oraz prędkość początkowa v1 = v0, to oznaczając t2=t i v2 = v, otrzymujemy a=(v-v0)/t, z czego

Całkując ten wzór w zakresie od zera do dowolnego momentu czasu t, stwierdzamy, że długość drogi przebytej przez punkt w przypadku ruchu jednostajnie zmiennego

3)aτ=f(t), an=0 - ruch prostoliniowy ze zmiennym przyspieszeniem;

4)aτ=0, an=stała. Gdy aτ=0, prędkość nie zmienia się w wartości bezwzględnej, ale zmienia się w kierunku. Ze wzoru an=v2/r wynika, że ​​promień krzywizny musi być stały. Dlatego ruch kołowy jest ruchem jednostajnym krzywoliniowym;

5)aτ=0, an≠0 ruch jednostajny krzywoliniowy;

6)aτ=const, an≠0 - krzywoliniowy ruch jednostajny;

7)aτ=f(t), an≠0 - ruch krzywoliniowy ze zmiennym przyspieszeniem.

Nr 18 Równania płaszczyzny stycznej i normalnej do powierzchni

Definicja. Niech funkcja dwóch zmiennych z =f(x,y) będzie dana w dziedzinie D, M0(x0;y0) będzie punktem wewnętrznym dziedziny D, M(x0+Δx;y+Δy) będzie punktem w dziedzinie D „sąsiadujący” M0.

Rozważ pełny przyrost funkcji:

Jeśli Δz jest reprezentowane jako:

gdzie A, B są stałymi (niezależnymi od Δx, Δy), - odległość pomiędzy M i M0, α(Δ x, Δy) - nieskończenie mała przy Δx 0, Δy 0; wówczas funkcję z =f(x,y) nazywa się różniczkowalną w punkcie M0 i wyrażenie

nazywa się całkowitą różniczką funkcji z =f(x;y) w punkcie M0.

Twierdzenie 1.1. Jeżeli z =f(x;y) jest różniczkowalne w punkcie M0, to

Dowód

Ponieważ w (1.16) Δx, Δy są dowolnymi nieskończenie małymi, możemy przyjąć Δy =0, Δx≠0, Δx 0, wówczas

po czym z (1.16) wynika

Podobnie zostało to udowodnione

oraz Twierdzenie 1.1. udowodniony.

Uwaga: różniczkowalność z =f(x,y) w punkcie M0 implikuje istnienie pochodnych cząstkowych. Twierdzenie odwrotne jest fałszywe (istnienie pochodnych cząstkowych w punkcie M0 nie implikuje różniczkowalności w punkcie M0).

W rezultacie, biorąc pod uwagę Twierdzenie 1.1, wzór (1.18) przyjmie postać:

Konsekwencja. Funkcja różniczkowalna w punkcie M0 jest w tym punkcie ciągła (z (1.17) wynika, że ​​dla Δx 0, Δy 0: Δz 0, z(M) z(M0)).

Uwaga: Podobnie w przypadku trzech lub więcej zmiennych. Wyrażenie (1.17) będzie miało postać:

Używanie znaczenie geometryczne(Rys. 1.3) pochodne cząstkowe i możemy otrzymać równanie (1.24) płaszczyzny stycznej πcass do powierzchni: z =f(x,y) w punkcie C0(x0,y0,z0), z0=z(M ):

Z porównania (1.24) i (1.21) otrzymujemy znaczenie geometryczne pełny mechanizm różnicowy funkcje dwóch zmiennych:

Przyrost z, gdy punkt C przemieszcza się wzdłuż płaszczyzny stycznej od punktu C0 do punktu

skąd jest (1.24).

Równanie normalnej Lн do powierzchni: z = f(x,y) w punkcie C0 otrzymuje się jako równanie prostej przechodzącej przez C0 prostopadle do płaszczyzny stycznej:

Nr 19 Pochodna kierunkowa. Gradient

Niech funkcja będzie podana w jakiejś dziedzinie i okres . Narysujmy wektor z punktu, którego kierunek jest cosinusem . Na wektorze, w pewnej odległości od jego początku, rozważ punkt, tj. .

Zakładamy, że funkcja a jego pochodne cząstkowe pierwszego rzędu są ciągłe w dziedzinie.

Granicę stosunku w nazywa się pochodną funkcji w tym punkcie w kierunku wektora i jest oznaczony, tj. .

Aby znaleźć pochodną funkcji w danym punkcie w kierunku wektora skorzystaj ze wzoru:

Gdzie – cosinusy kierunku wektora , które oblicza się według wzorów:
.

Niech funkcja będzie określona w każdym punkcie pewnego obszaru .

Wektor, którego rzuty na osie współrzędnych są wartościami pochodnych cząstkowych tej funkcji w odpowiednim punkcie, nazywany jest gradientem funkcji i jest oznaczony lub (czytaj „nabla u”): .

W tym przypadku mówią, że w regionie jest zdefiniowane pole wektorowe gradientów.

Aby znaleźć gradient funkcji w danym punkcie skorzystaj ze wzoru: .

Nr 22 podstawowe własności całki nieoznaczonej

Całka nieoznaczona

gdzie F jest funkcją pierwotną funkcji f (na przedziale); C jest dowolną stałą.

Podstawowe właściwości

1.

2.

3. Jeśli To

24)

25)

28)

Metodę tę stosuje się w przypadkach, gdy całka jest iloczynem lub ilorazem funkcji heterogenicznych. W tym przypadku za V’(x) przyjmuje się część, którą można łatwo zintegrować.

29)

32) Rozkład ułamka wymiernego na ułamki proste.

Dowolny ułamek wymierny właściwy
można przedstawić jako sumę skończonej liczby prostych ułamków wymiernych pierwszego – czwartego typu. Do rozkładu
konieczne jest rozwinięcie mianownika na ułamki proste Qm(x) na czynniki liniowe i kwadratowe, dla których należy rozwiązać równanie:

- (5)

Twierdzenie.Właściwy ułamek wymierny
, Gdzie
, można jednoznacznie rozłożyć na sumę ułamków prostych:

- (6)

(A 1 , A 2 , …, A k , B 1 , B 2 , …, B 1 , M 1 , N 1 , M 2 , M 2 , …, M s , N s – niektóre liczby rzeczywiste).

33) Rozkład ułamka właściwego na ułamki proste ze złożonymi pierwiastkami mianownika

Opis problemu. Znajdź całkę nieoznaczoną

1 . Wprowadźmy następującą notację:

Porównajmy stopnie licznika i mianownika.

Jeśli całka jest ułamkiem niewłaściwym wymiernym, tj. stopień licznikaN większa lub równa potęgi mianownikaM , to najpierw wybieramy całą część funkcji wymiernej, dzieląc licznik przez mianownik:

Tutaj wielomian jest resztą dzielenia przez i stopieńPk(x) mniejszy stopieńQm

2 . Rozwińmy właściwy ułamek wymierny

do ułamków elementarnych.

Jeśli jego mianownik jest liczbą pierwszą złożone korzenie te.

wtedy rozwinięcie ma postać

3 . Aby obliczyć niepewne współczynniki,A1,A2,A3...B1,B1,B3... sprowadzamy ułamek po prawej stronie tożsamości do wspólnego mianownika, po czym przyrównujemy współczynniki do tych samych potęgX w licznikach po lewej i prawej stronie. Weźmy system 2 S równania z 2 S nieznany, który ma unikalne rozwiązanie.

4 Całkujemy ułamki elementarne formy

47) Jeśli istnieje skończona granica I sumy całkowej jako λ → 0 i nie zależy ona od sposobu wyboru punktów ξ i, sposobu podziału odcinka, to granicę tę nazywa się całką oznaczoną funkcji f ( x) nad segmentem i oznacza się następująco:

W tym przypadku mówi się, że funkcja f (x) jest całkowalna na . Liczby a i b nazywane są odpowiednio dolną i górną granicą całkowania, f (x) jest całką, x jest zmienną całkowania. Należy zauważyć, że nie ma znaczenia, która litera oznacza zmienną całkującą całki oznaczonej

ponieważ zmiana tego rodzaju zapisów w żaden sposób nie wpływa na zachowanie sumy całkowej. Pomimo podobieństwa w notacji i terminologii, pewne i Całki nieoznaczone różny

48) Twierdzenie o istnieniu całki oznaczonej

Podzielmy odcinek na części za pomocą punktów x1,x2,x3... tak

Oznaczmy przez deltaX długość i-tego odcinka i maksimum tych długości.

Wybierzmy dowolnie określony punkt na każdym segmencie (nazywa się to „punktem środkowym”) i skomponujmy

wielkość zwaną sumą całkowitą

Znajdźmy teraz granicę

Definicja. Jeśli istnieje i nie zależy od tego

a) sposób podziału odcinka na części i z

b) sposób wyboru punktu środkowego,

jest całką oznaczoną funkcji f(x) po segmencie .

Funkcja f(x) nazywana jest w tym przypadku całkowalną na przedziale. Wielkości a i b nazywane są odpowiednio dolną i górną granicą całkowania.

50) Podstawowe własności całki oznaczonej

1) Jeżeli przedział całkowania dzielimy na skończoną liczbę przedziałów cząstkowych, to całka oznaczona po tym przedziale jest równa sumie całek oznaczonych po wszystkich jego przedziałach cząstkowych.

2) twierdzenie o wartości średniej.

Niech funkcja y = f(x) będzie całkowalna na przedziale ,m=min f(x) i M=max f(x), to istnieje taka liczba

Konsekwencja.

Jeżeli funkcja y = f(x) jest ciągła na przedziale , to istnieje liczba taka, że.

3) Po zmianie granic całkowania całka oznaczona zmienia swój znak na przeciwny.

4) Całka oznaczona przy tych samych granicach całkowania jest równa zeru.

5)Integracja modułu funkcyjnego

Jeżeli funkcja f(x) jest całkowalna, to jej moduł jest także całkowalny na przedziale.

6)Całkowanie nierówności

Jeśli f(x) i q(x) są całkowalne w przedziale, do którego należy x

To

7)Liniowość

Stały współczynnik można przyjąć poza znak całki oznaczonej

jeśli f(x) istnieje i jest całkowalne na przedziale, A=const

Jeżeli funkcja y=f(x) jest ciągła na pewnym przedziale i F(x) jest którąkolwiek z jej funkcji pierwotnych na (F’(x)=f(x)), to wzór jest spełniony

Pozwolić, aby obliczyć całkę funkcja ciągła dokonuje się podstawienia x=α(t).

1) Funkcja x=α(t) i jej pochodna x’=α’(t) są ciągłe dla t należącego do

2) Zbiór wartości funkcji x=α(t) w t należy do segmentu

3) A α(c)=a i α(v)=b

Niech funkcja f(x) będzie ciągła na tym przedziale i będzie miała nieskończoną nieciągłość w x=b. Jeżeli granica istnieje, nazywa się ją całką niewłaściwą drugiego rodzaju i oznacza się ją przez .

Zatem z definicji

Jeżeli istnieje granica po prawej stronie, to całka niewłaściwa zbiega się. Jeśli określona granica nie istnieje lub jest nieskończona, wówczas mówią, że całka różni się.

Pobierz z plików depozytowych

GEOMETRIA RÓŻNICZKOWA

I. FUNKCJA WEKTOROWA ARGUMENTU SKALARNEGO

Funkcja wektorowa (definicja 1.1), metody jej wyznaczania.

Wektor promienia i hodograf, specyfikacja hodografu parametrycznego.

Pochodna funkcji wektorowej (Definicja 1.6).

Znaczenie geometryczne pochodnej funkcji wektorowej.

Zasady różniczkowania funkcji wektorowych.

1.1. DEFINICJA FUNKCJI WEKTOROWEJ

Definicja 1.1Jeśli każda wartość argumentu skalarnegodopasowany wektor
przestrzeń trójwymiarowa R 3 , to mówią, że funkcja wektorowa (lub funkcja wektorowa) argumentu skalarnego jest dana na zbiorze XT .

Jeśli w kosmosie R 3 dany układ kartezjański współrzędneO xyz , to zadaniem jest funkcja wektorowa
,
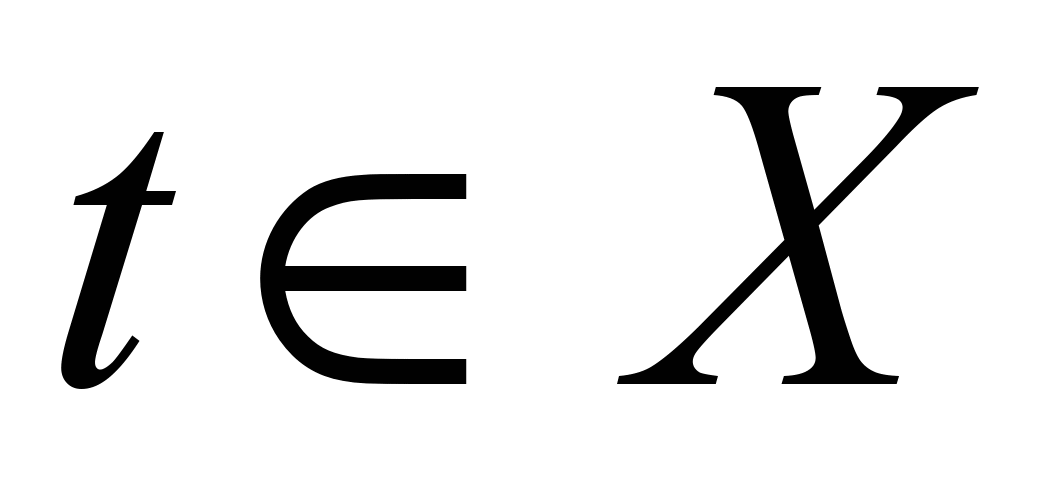jest równoznaczne z określeniem trzech funkcji skalarnychX( T ), y ( T ), z ( T ) – współrzędne wektora:

= { X ( T ), y ( T ), z ( T )} (1.1)

lub , (1.2)

Gdzie
— wektory jednostkowe współrzędnych.

1.2. LINIA PRZESTRZENNA JAKO HODOGRAF WEKTORA PROMIENIA

Definicja 1.2 Jeśli początkiem wszystkich wektorów jest ,umieszczone w początku układu, nazywane są wektorami promieniowymi.

Definicja 1.3 Linię będącą miejscem geometrycznym końców wektorów promienia , nazywamy hodografem funkcji wektorowej, a ich wspólnym początkiem jest biegun hodografu.

Jeżeli parametr T jest czasem i jest wektorem promienia poruszającego się punktu, wówczas hodografem funkcji jest trajektoria poruszającego się punktu.

Równanie hodografu można zapisać w postaci wektorowej (1.2) lub w postaci parametrycznej:

(1.3)

W szczególności, jeśli funkcja wektorowawraz ze zmianą argumentu zmienia się tylko jego moduł, ale kierunek się nie zmienia (), wówczas hodografem takiej funkcji wektorowej będzie promień prostoliniowy wychodzący z początku; jeśli tylko zmieni się kierunek wektora, ale jego wielkość pozostanie niezmieniona (
), wówczas hodografem funkcji wektorowej będzie krzywa położona na kuli o środku na biegunie i promieniu równym stałemu modułowi wektora.

Rysunek 1.

1.3. GRANICA, CIĄGŁOŚĆ I POCHODNA FUNKCJI WEKTOROWEJ

Definicja 1. 4 wektor nazywa się granicą funkcji wektorowejNa
, Jeśli

. (1.4)

Definicja 1.5 Nazywa się funkcję wektorową ciągły w pewnym punkcieT 0, jeśli ma w tym punkcie granicę równą wartości funkcji wektorowej w tym punkcie:

. (1.5)

Definicja 1.6Pochodna funkcji wektorowej w tym punkcie T nazywa się granicą stosunku przyrostu funkcji wektorowej do przyrostu argumentu
Na
:

(1.6)

1.4. ZNACZENIE GEOMETRYCZNE I MECHANICZNE PIERWSZEJ POCHODNEJ FUNKCJI WEKTOROWEJ

Znaczenie geometryczne pierwszej pochodnej funkcji wektorowej argumentu skalarnego jest takie, że pochodna ta jest nowym wektorem skierowanym stycznie do hodografu:
. Pokażmy to.

Rysunek 2

Zakładamy, że hodograf rozpatrywanej funkcji wektorowej jest linią ciągłą, która w dowolnym punkcie ma styczną.

Podajmy argument T przyrost, a następnie geometrycznie stosunek
jest jakimś wektorem
, leżący na siecznej MM”. Kiedy ten wektor obraca się i zamienia się w wektor
, leżącego na stycznej i skierowanego w kierunku rosnącymT . Zatem wektor

(1.7)

będzie jednostkowym wektorem stycznym zorientowanym w kierunku rosnącego parametruT .

Dlatego wektor
można przyjąć jako wektor kierunkowy styczny do krzywej w punkcie ), (lub
) i zapisz równanie styczne w postaci:

(1.8)

Jeśli T – czas i — wektor promienia punktu
, wprowadzając się przestrzeń trójwymiarowa, potem okołozależność nazywa się średnią prędkością punktu na odcinku [T; T+T].

Znaczenie mechanicznepierwsza pochodna funkcji wektorowej jest taka, że ​​pochodna ta reprezentuje prędkość punktu M w danej chwiliT :

Zasady różniczkowania funkcji wektorowych

Udowodnijmy regułę 1, korzystając z zasad odejmowania wektorów i dzielenia wektora przez liczbę:

Dowód pozostałych reguł opiera się na regule 1 i zasadach operowania wektorami.

Przykład 1.1: Biorąc pod uwagę funkcję wektorową.Skonstruuj jego hodograf i utwórz równanie jego stycznej w dowolnym punkcie.

Rozwiązanie. Dla dowolnego punktu ( X , y , z ) wektor hodografu – funkcje jakie mamy:X = koszt ; y = asint ; z = bt a zatem dla każdego
obowiązuje równośćX 2 + y 2 = A 2 , a tworząca jest równoległa do osi Oz. Jeżeli parametr T interpretowany jako czas, następnie przy ruchu jednostajnym po okręgu rzut końca wektora promienia na płaszczyznęOksy jego rzut na ośOz będzie poruszać się równomiernie i prostoliniowo z dużą prędkościąB . Inaczej mówiąc, zastosowanie punktu hodografu funkcji wektorowej rośnie proporcjonalnie do kąta obrotu jej rzutu na płaszczyznęOksy . Zatem pożądany hodograf będzie miał postać pokazaną na rys. 3 i nazywa się to linią helikalną. Aby znaleźć styczne do hodografu (linię śrubową), znajdujemy pochodną funkcji wektorowej.

Rozwiązanie. Od, Następnie

Przykład 2. Rozważmy na przykład funkcję trzech zmiennych F(X,Na,z), mając następującą tabelę prawdy:

Z porządkiem leksykograficznym wektorów wartości zmiennych  X N można je pominąć, a funkcja zostanie całkowicie określona przez własną funkcję wektor wartości logicznych F= (10110110).

Metoda matrycowa

Rzecz w tym, że jest wiele zmiennych  X N rozpada się na dwie części  Na M I  z n–m w taki sposób, aby wszystkie możliwe wartości logiczne wektora  Na M są wykreślane wzdłuż rzędów macierzy i wszystkich możliwych wartości logicznych wektora  z n - m- według kolumn. Wartości logiczne funkcji F na każdym zestawie   N = ( 1 , ...,  M ,  m+ 1 ,...,  N) umieszczone w komórkach utworzonych przez przecięcie linii ( 1 , ...,  M) i kolumna ( m+ 1 ,...,  N).

W omówionym powyżej przykładzie 2, w przypadku zmiennych dzielących ( x, y, z) na podzbiory ( X) I ( y, z) macierz ma postać:

	y,z

Istotną cechą metody macierzowej jest to, że kompletuje zbiory zmiennych  X N, odpowiadające sąsiadującym (zarówno w pionie, jak i w poziomie) komórkom, różnią się jedną współrzędną.

Określanie użycia pełnego drzewa binarnego

Do opisu N-funkcja lokalna F( X N) używana jest właściwość drzewa binarnego wysokość N, co polega na tym, że każdy znajdujący się w nim wierzchołek wiszący odpowiada w stosunku jeden do jednego pewnemu zbiorowi wartości wektorowych  X N. W związku z tym temu wiszącemu wierzchołkowi można przypisać tę samą wartość logiczną, jaką ma funkcja w tym zbiorze F. Jako przykład (rys. 1.3) przedstawiamy zadanie wykorzystujące omówione powyżej drzewo binarne funkcji trójskładnikowej f =(10110110).

Pierwszy rząd liczb przypisany do wiszących wierzchołków drzewa oznacza numer leksykograficzny zbioru, drugi - sam zbiór, a trzeci - wartość znajdującej się na nim funkcji.

Zadanie za pomocąN - sześcian jednostkowy wymiaruW N

Od szczytów W N można również odwzorować jeden do jednego na zbiór wszystkich zbiorów  X N, To N-funkcja lokalna F(X N) można określić, przypisując jego wartości logiczne odpowiednim wierzchołkom sześcianu W N . Rysunek 1.4 przedstawia ustawienie funkcji F= (10110110) na kostce W 3. Wierzchołom sześcianu przypisane są wartości prawdy.

Definicja . Algebra logiki nazwij zbiór stałych i zmiennych logicznych wraz z wprowadzonymi na nich łącznikami logicznymi.

Zadanie formułowe

Funkcje algebry logicznej można określić jako wyrażenia analityczne.

Definicja. Pozwalać X― alfabet zmiennych i stałych stosowanych w algebrze logicznej, F― zbiór oznaczeń wszystkich funkcji elementarnych i ich uogólnień z liczbą zmiennych przekraczającą 2.

Formuła na X, F(wzór na algebrę logiczną) nazwijmy wszystkie rekordy formularza:

A) X, Gdzie X X;

b)  F 1 , F 1 &F 2 ,F 1 F 2 , F 1 F 2 , F 1  F 2 , F 1 F 2 ,F 1 F 2 ,F 1 F 2 , Gdzie F 1 , F 2 - koniec formuł X, F;

V) H(F 1 , … ,F N ), Gdzie N > 2, F 1 ,… ,F N- koniec formuł X,F, H ― oznaczenie uogólnionej funkcji progowej z F .

Jak wynika z definicji, dla dwumiejscowych funkcji elementarnych stosuje się notację wrostkową, w której pomiędzy argumentami umieszcza się symbol funkcjonalny, w przypadku funkcji negacji i uogólnionej stosuje się przedrostkową formę zapisu, w której symbol funkcjonalny jest umieszczany przed listą argumentów.

Przykład 3.

1. Wyrażenia X(Naz); ( X, y, z  ty) są wzorami algebry logicznej, gdyż spełniają definicję podaną powyżej.

2. Wyrażenie  X (Na z) nie jest wzorem algebry logicznej, ponieważ operacja  została zastosowana niepoprawnie .

Definicja. Funkcja realizowana przez wzór F, jest funkcją uzyskaną przez podstawienie wartości zmiennych do F. Oznaczmy to F(F).

Przykład 4. Rozważ formułę F=xy (Xz). W celu skonstruowania tablicy prawdy zaimplementowanej funkcji należy wykonać mnożenie logiczne sekwencyjnie, biorąc pod uwagę siłę spójników logicznych xy, to implikacja ( Xz), następnie dodaj powstałe wartości prawdy modulo 2. Wynik działań pokazano w tabeli:

				X z

Formuła reprezentacji funkcji pozwala na ocenę a priori wielu właściwości funkcji. Przejście od zadania formułowego do tablicy prawdy zawsze można dokonać poprzez kolejne podstawienia wartości logicznych do funkcji elementarnych zawartych we wzorze. Przejście odwrotne jest niejednoznaczne, ponieważ tę samą funkcję można przedstawić za pomocą różnych wzorów. Wymaga osobnego rozważenia.

Definicja 1. Wektor r nazywa się funkcją wektorową argumentu skalarnego t, jeśli każda wartość skalara z zakresu dopuszczalnych wartości odpowiada pewnej wartości wektora r. Zapiszemy to w ten sposób: Jeśli wektor r jest funkcją argumentu skalarnego t, wówczas współrzędne x, y, z wektora r będą również funkcjami argumentu t: Funkcja wektorowa argumentu skalarnego. Hodograf. Granica i ciągłość funkcji wektorowej argumentu skalarnego. I odwrotnie, jeśli współrzędne wektora g są funkcjami t%, to sam wektor g będzie funkcją t: Zatem określenie funkcji wektorowej r(f) wynosi równoważne określeniu trzech funkcji skalarnych y(t), z(t). Definicja 2. Hodograf funkcji wektorowej r(t) argumentu skalarnego to zbiór punktów opisujący koniec wektora r(*) przy zmianie skalara t, gdy początek wektora r(f) wynosi umieszczony w stałym punkcie O w przestrzeni (rys. I ). Hodograf ze względu na ruch wektora wąsów r = g(*) Rys. 1 płonący punkt będzie trajektorią L samego tego punktu. Hodograf prędkości v = v(J) tego punktu będzie inną linią L\ (ryc. 2). Zatem jeśli punkt materialny porusza się po okręgu ze stałą prędkością |v| = const, to hodograf prędkości jest również okręgiem o środku w punkcie 0\ i promieniu równym |v|. Przykład 1. Zbuduj hodograf wektora r = ti + t\ + t\. Rozwiązanie. 1. Konstrukcję tę można wykonać punkt po punkcie, tworząc tabelę: Ryc. 3 2i Możesz zrobić to samo. Oznaczając współrzędne wektora V przez x, y, z otrzymamy Hts I kluczem do tych równań jest parametr 1Y otrzymujemy równania powierzchni y - z = x1, których linia przecięcia L wyznaczy hodograf wektora z() (rys. 3). D> Zadania dla. Konstruuj hodografy wektorów: Niech funkcja wektorowa r = argument skalarny t będzie zdefiniowana w pewnym sąsiedztwie wartości argumentu t, z wyjątkiem być może dla tej samej wartości rozszerzenia 1. Wektor stały А nazywany jest granicą wektor r(t), gdy dla dowolnego e > 0 istnieje b > 0 takie, że dla wszystkich t φ spełniających warunek 11, nierówność jest spełniona. Podobnie jak w analizie konwencjonalnej, napisz limr(0=A. Rys. 4 Geometrycznie , oznacza to, że wektor) as t -* to dąży do wektora And zarówno pod względem długości, jak i kierunku (ryc. 4). Definicja 2. Mówi się, że wektor a(£) jest nieskończenie mały w t -» to jeśli a(£) ma granicę w t -* to i granica ta jest równa zeru: Funkcja wektorowa argumentu skalarnego. Hodograf. Granica i ciągłość funkcji wektorowej argumentu skalarnego lub, co jest takie samo, dla dowolnego e istnieje 6 > 0 takie, że dla każdego t Ф spełniającego warunek nierówność |a(£)| Przykład 1. Pokaż, że wektor jest nieskończenie szkarłatnym wektorem dla t -* 0. Rozwiązanie. Mamy gdzie jest jasne, że jeśli dla dowolnego e 0 przyjmiemy 6 = ~, to w -0| zaznaczymy |. Zgodnie z definicją oznacza to, że a(t) jest wektorem nieskończonym w t 0. 1> problemy z niezależnym rozwiązaniem r. Pokaż, że granica modułu wektora jest równa modułowi jego granicy, jeśli ta ostatnia granica istnieje. . Udowodnić, że aby funkcja wektorowa r(*) miała granicę A w do, konieczne i wystarczające jest, aby r(można było przedstawić jako funkcję wektorową argumentu skalarnego. Hodograph. Granica i ciągłość funkcji wektorowej argument skalarny de a( t) jest wektorem nieskończonym dla t -* t0 14. Funkcja wektorowa a+ b(*) jest ciągła dla t = t0. Czy z tego wynika, że ​​wektory a(t) i b(J) są także ciągłe dla t - to? 15. Udowodnić, że jeśli a( są ciągłymi funkcjami wektorowymi, to ich iloczyn skalarny (a(*),b(f)) i iloczyn wektorowy |a(f),b(t)] są również ciągłe.