Dom
Fasady szklane
Równanie prostej, wzdłuż której przecinają się płaszczyzny. Równania prostej w przestrzeni. Własności macierzy odwrotnych

Równanie prostej, wzdłuż której przecinają się płaszczyzny. Równania prostej w przestrzeni. Własności macierzy odwrotnych

W tej części będziemy kontynuować badanie tematu równania prostej w przestrzeni z perspektywy stereometrii. Oznacza to, że linię prostą w przestrzeni trójwymiarowej będziemy uważać za linię przecięcia dwóch płaszczyzn.

Zgodnie z aksjomatami stereometrii, jeśli dwie płaszczyzny nie pokrywają się i mają jedną wspólny punkt, to i one mają jedną wspólną prostą, na której leżą wszystkie punkty wspólne obu płaszczyznom. Korzystając z równań dwóch przecinających się płaszczyzn, możemy wyznaczyć linię prostą układ prostokątny współrzędne

Rozważając temat, podamy liczne przykłady, szereg ilustracji graficznych i szczegółowych rozwiązań niezbędnych do lepszego przyswojenia materiału.

Niech zostaną dane dwie płaszczyzny, które nie pokrywają się ze sobą i przecinają. Oznaczmy je jako płaszczyznę α i płaszczyznę β. Umieśćmy je w prostokątnym układzie współrzędnych O x y z przestrzeń trójwymiarowa.

Jak pamiętamy, dowolną płaszczyznę w prostokątnym układzie współrzędnych wyznacza się ogólnym równaniem płaszczyzny w postaci A x + B y + C z + D = 0. Zakładamy, że płaszczyzna α odpowiada równaniu A 1 x + B 1 y + C 1 z + D 1 = 0, a płaszczyzna β odpowiada równaniu A 2 x + B 2 y + C 2 z + D 2 = 0. W tym przypadku wektory normalne płaszczyzn α i β n 1 → = (A 1, B 1, C 1) i n 2 → = (A 2, B 2, C 2) nie są współliniowe, ponieważ płaszczyzny tak nie pokrywają się ze sobą, a e są umieszczone równolegle do siebie. Zapiszmy ten warunek w następujący sposób:

n 1 → ≠ λ n 2 → ⇔ ZA 1 , b 1 , do 1 ≠ λ ZA 2 , λ b 2 , λ do 2 , λ ∈ R

Aby odświeżyć pamięć materiału na temat „Równoległość płaszczyzn”, zobacz odpowiednią sekcję naszej strony internetowej.

Oznaczmy literą linię przecięcia płaszczyzn A . Te. a = α ∩ β. Linia ta reprezentuje zbiór punktów wspólnych dla obu płaszczyzn α i β. Oznacza to, że wszystkie punkty prostej a spełniają oba równania płaszczyzny A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0. W rzeczywistości są one szczególnym rozwiązaniem układu równań A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.

Rozwiązanie ogólne układ równań liniowych A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 określa współrzędne wszystkich punktów linii, wzdłuż której znajdują się dwie płaszczyzny α i β przecinają się . Oznacza to, że za jego pomocą możemy wyznaczyć położenie prostej w prostokątnym układzie współrzędnych O x y z.

Rozważmy ponownie opisaną teorię, teraz na konkretnym przykładzie.

Przykład 1

Linia prosta O x jest linią prostą, wzdłuż której przecinają się płaszczyzny współrzędnych O x y i O x z. Zdefiniujmy płaszczyznę O x y równaniem z = 0, a płaszczyznę O x z równaniem y = 0. Omówiliśmy to podejście szczegółowo w rozdziale „Niekompletne ogólne równanie płaszczyzny”, aby w razie trudności można było ponownie sięgnąć do tego materiału. W tym przypadku oś współrzędnych O x wyznacza się w trójwymiarowym układzie współrzędnych za pomocą układu dwóch równań postaci y = 0 z = 0.

Znalezienie współrzędnych punktu leżącego na prostej, wzdłuż której przecinają się płaszczyzny

Rozważmy problem. Niech w przestrzeni trójwymiarowej będzie dany prostokątny układ współrzędnych O x y z. Linię, wzdłuż której przecinają się dwie płaszczyzny, wyznacza układ równań A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0. Dany punkt w przestrzeni trójwymiarowej M 0 x 0, y 0, z 0.

Ustalmy, czy punkt M 0 x 0, y 0, z 0 należy do danej prostej A .

Aby uzyskać odpowiedź na pytanie, jakie jest zadanie, podstawiamy współrzędne punktu M 0 do każdego z dwóch równań płaszczyzny. Jeżeli w wyniku podstawienia oba równania zamienią się w prawidłowe równości A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 i A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0, wówczas punkt M 0 należy do każdej z płaszczyzn i należy do danej prostej. Jeśli choć jedna z równości A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 i A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 okaże się fałsz, to punkt M 0 nie należy do prostej.

Spójrzmy na przykładowe rozwiązanie

Przykład 2

Linię prostą w przestrzeni definiują równania dwóch przecinających się płaszczyzn postaci 2 x + 3 y + 1 = 0 x - 2 y + z - 3 = 0. Ustal, czy punkty M 0 (1, - 1, 0) i N 0 (0, - 1 3, 1) należą do linii prostej przecięcia płaszczyzn.

Rozwiązanie

Zacznijmy od punktu M 0. Podstawmy jego współrzędne do obu równań układu 2 · 1 + 3 · (- 1) + 1 = 0 1 - 2 · (- 1) + 0 - 3 = 0 ⇔ 0 = 0 0 = 0 .

W wyniku podstawienia otrzymaliśmy prawidłowe równości. Oznacza to, że punkt M 0 należy do obu płaszczyzn i leży na linii ich przecięcia.

Podstawmy współrzędne punktu N 0 (0, - 1 3, 1) do obu równań płaszczyzny. Otrzymujemy 2 0 + 3 - 1 3 + 1 = 0 0 - 2 - 1 3 + 1 - 3 = 0 ⇔ 0 = 0 - 1 1 3 = 0.

Jak widać drugie równanie układu stało się równaniem niepoprawnym. Oznacza to, że punkt N 0 nie należy do danej prostej.

Odpowiedź: punkt M 0 należy do linii prostej, ale punkt N 0 nie.

Teraz oferujemy algorytm znajdowania współrzędnych pewnego punktu należącego do linii prostej, jeśli prosta w przestrzeni w prostokątnym układzie współrzędnych O x y z jest określona równaniami przecinających się płaszczyzn A 1 x + B 1 y + C 1 z + re 1 = 0 ZA 2 x + b 2 y + do 2 z + re 2 = 0 .

Liczba rozwiązań układu dwóch równań liniowych z niewiadomymi A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 jest nieskończona. Każde z tych rozwiązań może być rozwiązaniem problemu.

Podajmy przykład.

Przykład 3

Niech linię prostą w przestrzeni trójwymiarowej zdefiniują równania dwóch przecinających się płaszczyzn postaci x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0. Znajdź współrzędne dowolnego punktu na tej prostej.

Rozwiązanie

Przepiszmy układ równań x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 .

Weźmy niezerową mollę drugiego rzędu jako moll bazowy macierzy głównej układu 1 0 2 3 = 3 ≠ 0. To oznacza, że z jest nieznaną zmienną wolną.

Przesuńmy wyrazy zawierające niewiadomą wolną z na prawą stronę równań:

x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 ⇔ x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z

Wprowadźmy dowolną liczbę rzeczywistą λ i załóżmy, że z = λ.

Wtedy x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z ⇔ x + 0 y = - 7 - 3 λ 2 x + 3 y = - 2 - 3 λ .

Aby rozwiązać powstały układ równań, stosujemy metodę Cramera:

∆ = 1 0 2 3 = 1 3 - 0 1 = 2 ∆ x = - 7 - 3 λ 0 - - 3 λ 3 = - 7 - 3 λ 3 - 0 (- 2 - 3 λ) = 21 - 9 λ ⇒ x = ∆ x ∆ = - 7 - 3 λ ∆ y = 1 - 7 - 3 λ 2 - 2 - 3 λ = 1 · - 2 - 3 λ - - 7 - 3 λ = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

Ogólne rozwiązanie układu równań x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 będzie miało postać x = - 7 - 3 λ y = 4 + λ z = λ, gdzie λ ∈ R.

Aby otrzymać konkretne rozwiązanie układu równań, które da nam pożądane współrzędne punktu należącego do danej prostej, musimy przyjąć określoną wartość parametru λ. Jeśli λ = 0, to x = - 7 - 3 0 y = 4 + 0 z = 0 ⇔ x = - 7 y = 4 z = 0.

Pozwala nam to uzyskać współrzędne pożądanego punktu - 7, 4, 0.

Sprawdźmy dokładność znalezionych współrzędnych punktu, podstawiając je do oryginalnych równań dwóch przecinających się płaszczyzn - 7 + 3 · 0 + 7 = 0 2 · (- 7) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .

Odpowiedź: - 7 , 4 , 0

Wektor kierunkowy linii, wzdłuż której przecinają się dwie płaszczyzny

Przyjrzyjmy się, jak określić współrzędne wektora kierunkowego linii prostej, które są określone przez równania dwóch przecinających się płaszczyzn A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + do 2 z + re 2 = 0. W prostokątnym układzie współrzędnych 0xz wektor kierunkowy linii prostej jest nierozerwalnie związany z linią prostą.

Jak wiemy, prosta jest prostopadła do płaszczyzny w przypadku, gdy jest prostopadła do dowolnej prostej leżącej w danej płaszczyźnie. Z powyższego wynika, że ​​wektor normalny płaszczyzny jest prostopadły do ​​dowolnego niezerowego wektora leżącego w danej płaszczyźnie. Te dwa fakty pomogą nam w znalezieniu wektora kierunku linii.

Płaszczyzny α i β przecinają się wzdłuż linii A . Wektor kierunku a → linia prosta A położony prostopadle do wektora normalnego n 1 → = (A 1 , B 1 , C 1) płaszczyzny A 1 x + B 1 y + C 1 z + D 1 = 0 i wektora normalnego n 2 → = (A 2 , B 2, C 2) płaszczyzny A 2 x + B 2 y + C 2 z + re 2 = 0.

Wektor bezpośredni A jest iloczynem wektorowym wektorów n → 1 = (A 1, B 1, C 1) i n 2 → = A 2, B 2, C 2.

za → = n → 1 × n 2 → = ja → jot → k → ZA 1 b 1 do 1 za 2 b 2 do 2

Zdefiniujmy zbiór wszystkich wektorów kierujących linii jako λ · a → = λ · n 1 → × n 2 → , gdzie λ jest parametrem, który może przyjmować dowolne wartości rzeczywiste inne niż zero.

Przykład 4

Niech prostą w przestrzeni w prostokątnym układzie współrzędnych O x y z wyznaczają równania dwóch przecinających się płaszczyzn x + 2 y - 3 z - 2 = 0 x - z + 4 = 0. Znajdźmy współrzędne dowolnego wektora kierunku tej linii.

Rozwiązanie

Płaszczyzny x + 2 y - 3 z - 2 = 0 i x - z + 4 = 0 mają wektory normalne n 1 → = 1, 2, - 3 i n 2 → = 1, 0, - 1. Za wektor kierunkowy przyjmijmy linię prostą, która jest przecięciem dwóch dane samoloty, iloczyn wektorowy wektorów normalnych:

a → = n → 1 × n 2 → = ja → jot → k → 1 2 - 3 1 0 - 1 = ja → · 2 · (- 1) + jot → · (- 3) · 1 + k → · 1 · 0 - - k → · 2 · 1 - j → · 1 · (- 1) - i → · (- 3) · 0 = - 2 · ja → - 2 jot → - 2 k →

Zapiszmy odpowiedź w postaci współrzędnych a → = - 2, - 2, - 2. Tym, którzy nie pamiętają, jak to zrobić, zalecamy zapoznanie się z tematem „Współrzędne wektorowe w prostokątnym układzie współrzędnych”.

Odpowiedź: a → = - 2 , - 2 , - 2

Przejście do równań parametrycznych i kanonicznych prostej w przestrzeni

Do rozwiązania szeregu problemów łatwiej jest zastosować równania parametryczne prostej w przestrzeni postaci x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ lub równania kanoniczne linia prosta w przestrzeni postaci x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ. W tych równaniach a x, a y, a z są współrzędnymi wektora kierującego linii, x 1, y 1, z 1 są współrzędnymi pewnego punktu na linii, a λ jest parametrem przyjmującym dowolne wartości rzeczywiste.

Z równania prostego postaci A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 możemy przejść do równań kanonicznych i parametrycznych linia prosta w przestrzeni. Do napisania równań kanonicznych i parametrycznych linii prostej będziemy potrzebować umiejętności znajdowania współrzędnych określonego punktu na prostej, a także współrzędnych pewnego wektora kierującego linii prostej, określonych równaniami dwie przecinające się płaszczyzny.

Spójrzmy na to, co napisano powyżej na przykładzie.

Przykład 5

Zdefiniujmy linię prostą w trójwymiarowym układzie współrzędnych za pomocą równań dwóch przecinających się płaszczyzn 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0. Napiszmy równania kanoniczne i parametryczne tej prostej.

Rozwiązanie

Znajdźmy współrzędne wektora kierującego linii, który jest iloczynem wektorowym wektorów normalnych n 1 → = 2, 1, - 1 płaszczyzny 2 x + y - z - 1 = 0 i n 2 → = ( 1, 3, - 2) płaszczyzny x + 3 y - 2 z = 0:

a → = n 1 → × n 2 → = ja → jot → k → 2 1 - 1 1 3 - 2 = ja → · 1 · (- 2) + jot → · (- 1) · 1 + k → · 2 · 3 - - k → · 1 · 1 - j → · 2 · (- 2) - i → · (- 1) · 3 = i → + 3 · jot → + 5 · k →

Współrzędne wektora kierującego prostej a → = (1, 2, 5).

Kolejnym krokiem jest wyznaczenie współrzędnych pewnego punktu na danej prostej, co jest jednym z rozwiązań układu równań: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ 2 x + y - z = 1 x + 3 y - 2 z = 0 .

Za małą macierz układu przyjmijmy wyznacznik 2 1 1 3 = 2 · 3 - 1 · 1 = 5, który jest niezerowy. W tym przypadku zmienna z jest bezpłatny. Przesuńmy z nim wyrazy na prawą stronę każdego równania i nadajmy zmiennej dowolną wartość λ:

2 x + y - z = 1 x + 3 y - 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ, λ ∈ R

Do rozwiązania otrzymanego układu równań wykorzystujemy metodę Cramera:

∆ = 2 1 1 3 = 2 3 - 1 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = (1 + λ) 3 - 1 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ - (1 + λ) · 1 = - 1 + 3 λ ⇒ y = ∆ y ∆ = - 1 + 3 λ 5 = - 1 5 + 3 5 λ

Otrzymujemy: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 y = - 1 5 + 3 5 z = λ

Przyjmijmy λ = 2, aby otrzymać współrzędne punktu na prostej: x 1 = 3 5 + 1 5 2 y 1 = - 1 5 + 3 5 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Teraz mamy wystarczająco dużo danych, aby zapisać równania kanoniczne i parametryczne danej prostej w przestrzeni: x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ x - 1 1 = y - 1 3 = z - 2 5 x = x 1 + za x · λ y = y 1 + za y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ

Odpowiedź: x - 1 1 = y - 1 3 = z - 2 5 i x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ

Istnieje inny sposób rozwiązania tego problemu.

Znalezienie współrzędnych określonego punktu na linii odbywa się poprzez rozwiązanie układu równań A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.

W ogólnym przypadku jej rozwiązania można zapisać w postaci żądanych równań parametrycznych prostej w przestrzeni x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ.

Równania kanoniczne otrzymujemy następująco: każde z otrzymanych równań rozwiązujemy ze względu na parametr λ i przyrównujemy prawe strony równości.

x = x 1 + a x · λ y = y 1 + za y · λ z = z 1 + a z · λ ⇔ λ = x - x 1 a x λ = y - y 1 za y λ = z - z 1 a z ⇔ x - x 1 za x = y - y 1 za y = z - z 1 za z

Zastosujmy tę metodę, aby rozwiązać problem.

Przykład 6

Wyznaczmy położenie prostej za pomocą równań dwóch przecinających się płaszczyzn 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0. Napiszmy równania parametryczne i kanoniczne dla tej prostej.

Rozwiązanie

Rozwiązywanie układu dwóch równań z trzema niewiadomymi przeprowadzamy analogicznie jak w poprzednim przykładzie. Otrzymujemy: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ .

Są to równania parametryczne linii w przestrzeni.

Równania kanoniczne otrzymujemy w następujący sposób: x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ ⇔ λ = x - 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x - 3 5 1 5 = y + 1 5 3 5 = z 1

Równania otrzymane w obu przykładach różnią się wyglądem, ale są równoważne, ponieważ definiują ten sam zbiór punktów w przestrzeni trójwymiarowej, a zatem tę samą linię prostą.

Odpowiedź: x - 3 5 1 5 = y + 1 5 3 5 = z 1 i x = 3 5 + 1 5 λ y = - 1 5 + 3 5 λ z = λ

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Ze względu na swoją wagę problem przecięcia płaszczyzn nazywany jest przez wielu autorów „problemem pozycyjnym nr 2”.

Ze stereometrii wiadomo, że linia przecięcia dwóch płaszczyzn jest linią prostą. W poprzednich zagadnieniach wstępnych, gdzie mówiliśmy o szczególnych przypadkach przecięcia płaszczyzn, wychodziliśmy z tej definicji.

Jak wiadomo, aby skonstruować tę czy inną linię, w najprostszym przypadku konieczne jest znalezienie dwóch punktów należących do tej prostej. W przypadku określenia płaszczyzny za pomocą śladów, te dwa punkty są punktami przecięcia tych samych śladów przecinających się płaszczyzn.

Przykłady samodzielnej pracy

Ćwiczenie 5.1

Skonstruuj linie przecięcia płaszczyzn wyznaczonych przez tory (ryc. 72):

  • a) wystające poziomo I i wystające do przodu A;
  • b) wystający poziomo Z i płaszczyzna ogólne stanowisko Q;
  • c) dwie płaszczyzny położenia ogólnego I i 0.

Ryż. 72

Na ryc. 73 zawiera odpowiedzi do tego ćwiczenia.

W przypadkach, gdy płaszczyzny są określone lokalnymi figurami płaszczyzny, wskazane jest zastosowanie co najmniej dwóch różnych ścieżek rozwiązania.


Ryż. 73

Pierwszym rozwiązaniem jest zastosowanie trójstopniowego algorytmu znajdowania punktu styku prostej ogólnej z płaszczyzną ogólną. Aby znaleźć linię przecięcia dwóch trójkątów, jeden z trójkątów pozostaje niezmieniony, a drugi jest mentalnie podzielony na osobne segmenty, przedstawiając je jako linie proste w ogólnym położeniu. Najpierw znajdź punkt przecięcia jednej z ogólnych linii z płaszczyzną trójkąta. Następnie znajdują kolejny brakujący punkt należący do żądanej linii. Odbywa się to w podobny sposób, powtarzając całą opisaną sekwencję czynności.

Ćwiczenie 5.2

Dane współrzędne wierzchołków dwóch trójkątów LAN I DEK skonstruuj diagram tego ostatniego i znajdź linię ich przecięcia. Wskaż na schemacie widoczność elementów obu trójkątów: A(0, 9, 2); ?(10, 1, 16); C (23, 14, 9); D(3, 17, 18); ?(22, 11, 17); ?(12,0, 2). Aby znaleźć linie przecięcia trójkątów, zaleca się najpierw znaleźć punkt przecięcia linii prostej KD z trójkątem ABC, a następnie punkt przecięcia linii prostej NE z trójkątem EDK.

Ogólny widok otrzymanego diagramu pokazano na ryc. 74.

Drugie rozwiązanie to zastosowanie dwóch pomocniczych płaszczyzn tnących poziomu.

Dane przecinające się figury płaskie należy przeciąć dwukrotnie płaszczyznami pomocniczymi (albo o tej samej nazwie, albo przeciwnej - nie ma to znaczenia), np. dwiema płaszczyznami poziomymi.

Łatwo zrozumieć, że jednorazowe rozcięcie pozwala znaleźć dwie przecinające się linie h l I i 2, dając jeden punkt A, należący do żądanej linii przecięcia (ryc. 75). Rysowanie kolejnej podobnej płaszczyzny pomocniczej w pewnej odległości

Ryż. 74


Ryż. 75

z pierwszego dostają podobną konstrukcję i jeszcze jeden punkt. Łącząc rzuty o tej samej nazwie dwóch uzyskanych punktów, znajduje się pożądaną linię przecięcia dwóch płaszczyzn.

Ćwiczenie 5.3

Korzystając z podanych współrzędnych punktów dwóch figur trójkątnych, skonstruuj diagram tej ostatniej, na którym za pomocą płaszczyzn pomocniczych skonstruuj linię przecięcia trójkątów. Wskaż na schemacie widoczność elementów obu trójkątów:

do ABC. A(16, 5, 17); Ja (10, 19,

A OBR: D (24, 12, 14); ? (4, 18,

Ogólny widok rozwiązanego problemu pokazano na rys. 76.

Ćwiczenie 5.4

Aby utrwalić umiejętność znajdowania linii przecięcia dwóch płaszczyzn, podano problem, którego rozwiązanie podano w dynamice konstrukcji zgodnie z etapami algorytmu.

Znajdź linię przecięcia dwóch płaszczyzn we wspólnym położeniu p to jq

określone przez dwa trójkąty ABC I OBR i określić widoczność ich wzajemnego przenikania się (ryc. 77).

Rozwiązanie przykładu sprowadza się do znalezienia punktów przecięcia boków (prostych) A ABC z płaszczyzną rodzajową podaną przez A OBR. Algorytm rozwiązania tego przykładu jest znany.

Kończymy bok (prosty) JAKO LAN w pomocniczą wystającą do przodu płaszczyznę t _1_ P 2 (ryc. 78).

Ślad czołowy tej płaszczyzny pomocniczej przecina rzuty boków D 2 mi 2 gE 2 - 1 2 i D 2 F 2 pt 2 = 2 2 w punktach 1 2 i 2 2 . Linie komunikacyjne projekcji umożliwiają wyznaczenie linii przecięcia (1 !~2 2) = n A na poziomej płaszczyźnie rzutów D X E X F ( . Następnie wskaż K 1 i jego projekcja K2 określić punkt przecięcia linii AC z A OBR.

Powtarzamy algorytm znajdowania punktu przecięcia boku A ABC bezpośredni Słoneczny z ADEFem. Zamykamy słońce w pomocniczej, wystającej do przodu płaszczyźnie p_L P 2 (ryc. 79).

Znajdujemy rzuty punktów 3 i 4 i na poziomą płaszczyznę rzutów wyznaczamy rzut punktu przecięcia prostej B1C [ z linią przecięcia (3,-4,):

Linia komunikacyjna projekcji pozwala na odnalezienie jej przedniego punktu projekcji M 2.

Łączenie znalezionych punktów Ki Mi znajdź linię przecięcia dwóch płaszczyzn ogólnych A ABC n A OBR= AF (ryc. 80).

Widoczność boków AABC stosunkowo ADEF ustalane na podstawie konkurencyjnych punktów. Najpierw określamy widoczność kształty geometryczne na płaszczyźnie projekcji P 2. Aby to zrobić, poprzez konkurencyjne punkty 5 i 6 (5 2 = 6 2) narysuj linię komunikacyjną projekcji prostopadle do osi projekcji x rz(ryc. 81).

Według rzutów poziomych 5 U I 6 { punkty 5 i 6, w których linia połączenia rzutu odpowiednio przecina linie przecinające się AC 4 D.F. okazuje się, że punkt 6 jest bardziej oddalony od płaszczyzny rzutu P 2 niż punkt 5. Zatem punkt 6 jest linią prostą D.F. do którego należy, są widoczne względem płaszczyzny projekcji P 2 . Wynika z tego, że segment (K 2 -6 2) będzie niewidoczny. Podobnie wyznaczamy widoczność boków A LAN i A DEF - niedz I D.F. te. segment (F 2 -8 2) będzie niewidoczny.

Widoczność AABC I ADEF względem płaszczyzny projekcji П j, ustala się w podobny sposób. Aby określić widoczność przecinających się linii AC*DF I BC ±DF względem płaszczyzny projekcji P] przez konkurujące ze sobą punkty 9 1 = 10 1 i 11 1 = 12 1 rysujemy linie komunikacyjne projekcji prostopadle x s. Na podstawie rzutów czołowych tych konkurujących punktów ustalamy, że rzuty punktów 10 2 i 12 2 są bardziej oddalone od płaszczyzny rzutu P ( . W związku z tym segmenty (А^-УД i (M g 2 1) będzie niewidoczny. Stąd widoczność AABC I ADEF jest wyraźnie pokazane na ryc. 82.

KĄT MIĘDZY PŁASZCZYZNAMI

Rozważmy dwie płaszczyzny α 1 i α 2, określone odpowiednio równaniami:

Pod kąt między dwiema płaszczyznami zrozumiemy jeden z kątów dwuściennych utworzonych przez te płaszczyzny. Oczywiste jest, że kąt między wektorami normalnymi a płaszczyznami α 1 i α 2 jest równy jednemu ze wskazanych sąsiednich kątów dwuściennych lub . Dlatego . Ponieważ I , To

.

Przykład. Określ kąt między płaszczyznami X+2y-3z+4=0 i 2 X+3y+z+8=0.

Warunek równoległości dwóch płaszczyzn.

Dwie płaszczyzny α 1 i α 2 są równoległe wtedy i tylko wtedy, gdy ich wektory normalne są równoległe, a zatem .

Zatem dwie płaszczyzny są do siebie równoległe wtedy i tylko wtedy, gdy współczynniki odpowiednich współrzędnych są proporcjonalne:

Lub

Warunek prostopadłości płaszczyzn.

Jest oczywiste, że dwie płaszczyzny są prostopadłe wtedy i tylko wtedy, gdy ich wektory normalne są prostopadłe, a zatem, lub .

Zatem, .

Przykłady.

PROSTO W PRZESTRZENI.

RÓWNANIE WEKTOROWE DLA LINII.

PARAMETRYCZNE RÓWNANIA BEZPOŚREDNIE

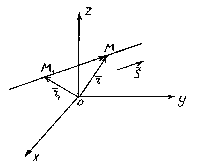
Położenie linii w przestrzeni jest całkowicie określane poprzez określenie dowolnego z jej punktów stałych M 1 i wektor równoległy do ​​tej prostej.

Nazywa się wektor równoległy do ​​prostej przewodniki wektor tej linii.

Więc niech linia prosta l przechodzi przez punkt M 1 (X 1 , y 1 , z 1), leżącego na prostej równoległej do wektora .

Rozważ dowolny punkt M(x,y,z) na linii prostej. Z rysunku wynika, że .

Wektory i są współliniowe, więc istnieje taka liczba T, co , gdzie jest mnożnik T może przyjmować dowolną wartość liczbową w zależności od położenia punktu M na linii prostej. Czynnik T zwany parametrem. Po wyznaczeniu wektorów promieni punktów M 1 i M odpowiednio poprzez i , otrzymujemy . To równanie nazywa się wektor równanie prostej. Pokazuje to dla każdej wartości parametru T odpowiada wektorowi promienia pewnego punktu M, leżąc na linii prostej.

Zapiszmy to równanie w postaci współrzędnych. Zauważ, że i stąd

Powstałe równania nazywane są parametryczny równania prostej.

Podczas zmiany parametru T współrzędne się zmieniają X, y I z i okres M porusza się po linii prostej.


RÓWNANIA KANONICZNE BEZPOŚREDNIEJ

Pozwalać M 1 (X 1 , y 1 , z 1) – punkt leżący na prostej l, I jest jego wektorem kierunkowym. Weźmy jeszcze raz dowolny punkt na prostej M(x,y,z) i rozważ wektor .

Oczywiste jest, że wektory są również współliniowe, więc odpowiadające im współrzędne muszą być proporcjonalne, dlatego

– kanoniczny równania prostej.

Uwaga 1. Należy zauważyć, że równania kanoniczne prostej można uzyskać z równań parametrycznych, eliminując parametr T. Rzeczywiście, z równań parametrycznych otrzymujemy Lub .

Przykład. Zapisz równanie prostej w formie parametrycznej.

Oznaczmy , stąd X = 2 + 3T, y = –1 + 2T, z = 1 –T.

Uwaga 2. Niech prosta będzie prostopadła do jednej z osi współrzędnych, na przykład osi Wół. Wtedy wektor kierunkowy linii jest prostopadły Wół, stąd, M=0. W rezultacie równania parametryczne linii przyjmą postać

Wyłączenie parametru z równań T, otrzymujemy równania prostej w postaci

Jednak i w tym przypadku zgadzamy się formalnie zapisać równania kanoniczne prostej w postaci . Zatem jeśli mianownik jednego z ułamków wynosi zero, oznacza to, że linia prosta jest prostopadła do odpowiedniej osi współrzędnych.

Podobnie jak w równaniach kanonicznych odpowiada linii prostej prostopadłej do osi Wół I Oj Lub równolegle do osi Oz.

Przykłady.

RÓWNANIA OGÓLNE PROSTEJ JAKO LINIE PRZECIĘCIA DWÓCH PŁASZCZYZN

Przez każdą linię prostą w przestrzeni przechodzi niezliczona ilość płaszczyzn. Dowolne dwa z nich, przecinające się, definiują to w przestrzeni. W konsekwencji równania dowolnych dwóch takich płaszczyzn, rozpatrywane łącznie, reprezentują równania tej prostej.

Ogólnie rzecz biorąc, podane są dowolne dwie nierównoległe płaszczyzny równania ogólne

wyznacz linię prostą ich przecięcia. Równania te nazywane są równania ogólne bezpośredni.

Przykłady.

Skonstruuj prostą określoną równaniami

Aby zbudować linię prostą, wystarczy znaleźć dowolne dwa jej punkty. Najłatwiej jest wybrać punkty przecięcia prostej z płaszczyznami współrzędnych. Na przykład punkt przecięcia z płaszczyzną xOj otrzymujemy z równań prostej, zakładając z= 0:

Po rozwiązaniu tego systemu znajdujemy sedno M 1 (1;2;0).

Podobnie, zakładając y= 0, otrzymujemy punkt przecięcia prostej z płaszczyzną xOz:

Z ogólnych równań prostej można przejść do jej równań kanonicznych lub parametrycznych. Aby to zrobić, musisz znaleźć jakiś punkt M 1 na linii prostej i wektor kierunkowy linii prostej.

Współrzędne punktu M 1 otrzymujemy z tego układu równań, nadając jednej ze współrzędnych dowolną wartość. Aby znaleźć wektor kierunku, należy pamiętać, że wektor ten musi być prostopadły do ​​obu wektorów normalnych I . Dlatego poza wektorem kierunkowym linii prostej l możesz wziąć iloczyn wektorowy normalnych wektorów:

.

Przykład. Podaj ogólne równania prostej do postaci kanonicznej.

Znajdźmy punkt leżący na prostej. W tym celu wybieramy dowolnie jedną ze współrzędnych, np. y= 0 i rozwiąż układ równań:

Wektory normalne płaszczyzn wyznaczających linię mają współrzędne Dlatego wektor kierunku będzie prosty

. Stąd, l: .


KĄT MIĘDZY PROSTYMI

Kąt pomiędzy liniami prostymi w przestrzeni nazwiemy dowolny z sąsiednich kątów utworzonych przez dwie linie proste poprowadzone przez dowolny punkt równoległy do ​​danych.

Niech w przestrzeni zostaną dane dwie proste:

Oczywiście kąt φ między prostymi można przyjąć jako kąt między ich wektorami kierunkowymi i . Ponieważ , to korzystając ze wzoru na cosinus kąta między wektorami otrzymujemy

Wprowadźmy równania kanoniczne prostej

współczynnik jest różny od zera, czyli linia prosta nie jest równoległa do płaszczyzny xOy. Zapiszmy te równania oddzielnie w następującej postaci:

W naszych warunkach równania (6) całkowicie definiują linię prostą. Każdy z nich indywidualnie wyraża płaszczyznę, przy czym pierwsza z nich jest równoległa do osi Oy, a druga do osi

Zatem przedstawiając prostą za pomocą równań postaci (6), uważamy ją za przecięcie dwóch płaszczyzn, które rzutują tę prostą na płaszczyznę współrzędnych xOz i yOz. Pierwsze z równań (6), rozpatrywane w płaszczyźnie, określa rzut danej prostej na tę płaszczyznę; w ten sam sposób drugie z równań (6), rozpatrywane w płaszczyźnie, wyznacza rzut danej prostej na płaszczyznę yOz. Można więc powiedzieć, że podanie równań prostej w postaci (6) oznacza podanie jej rzutu na płaszczyznę współrzędnych xOz i yOz.

Gdyby współczynnik wiodący wynosił zero, to na przykład co najmniej jeden z dwóch pozostałych współczynników byłby różny od zera, czyli linia prosta nie byłaby równoległa do płaszczyzny yOz. W tym przypadku moglibyśmy wyrazić linię prostą

równania płaszczyzn rzutując je na płaszczyzny współrzędnych, zapisując równania (5) w postaci

Zatem dowolną linię prostą można wyrazić równaniami dwóch przechodzących przez nią płaszczyzn i rzutujących ją na płaszczyzny współrzędnych. Ale wcale nie jest konieczne definiowanie linii prostej za pomocą takiej pary płaszczyzn.

Przez każdą linię prostą przechodzi niezliczona ilość płaszczyzn. Dowolne dwa z nich, przecinające się, definiują to w przestrzeni. W konsekwencji równania dowolnych dwóch takich płaszczyzn, rozpatrywane łącznie, reprezentują równania tej prostej.

Ogólnie rzecz biorąc, dowolne dwie płaszczyzny, które nie są do siebie równoległe, z ogólnymi równaniami

wyznacz linię prostą ich przecięcia.

Równania (7), rozpatrywane łącznie, nazywane są ogólnymi równaniami prostej.

Z ogólnych równań prostej (7) możemy przejść do jej równań kanonicznych. W tym celu musimy znać jakiś punkt na prostej i wektor kierunkowy.

Współrzędne punktu z danego układu równań możemy łatwo znaleźć, wybierając dowolnie jedną ze współrzędnych, a następnie rozwiązując układ dwóch równań, korzystając z wyrazów pozostałych dwóch współrzędnych.

Aby znaleźć wektor kierunkowy linii prostej, zauważamy, że wektor ten, skierowany wzdłuż linii przecięcia tych płaszczyzn, musi być prostopadły do ​​obu wektorów normalnych tych płaszczyzn. I odwrotnie, każdy wektor prostopadły do ​​jest równoległy do ​​obu płaszczyzn, a zatem do danej prostej.

Ale iloczyn wektorowy ma również tę właściwość. Dlatego iloczyn wektorowy wektorów normalnych tych płaszczyzn można przyjąć jako wektor kierujący linii prostej.

Przykład 1. Sprowadź równanie prostej do postaci kanonicznej

Wybierzmy jedną ze współrzędnych dowolnie. Niech np. Następnie

skąd Więc znaleźliśmy punkt (2, 0, 1) leżący na prostej,

Teraz znajdując iloczyn wektorowy wektorów, otrzymujemy wektor kierunkowy linii prostej. Dlatego równania kanoniczne będą miały postać:

Komentarz. Z ogólnych równań prostych postaci (7) można przejść do równań kanonicznych bez uciekania się do metody wektorowej.

Zatrzymajmy się najpierw bardziej szczegółowo na równaniach

Wyraźmy x i y z nich poprzez . Następnie otrzymujemy:

gdzie powinno być

Równania (6) w rzutach na płaszczyznę nazywane są równaniami prostymi

Zainstalujmy znaczenie geometryczne stałe M i N: M oznacza współczynnik kątowy rzutu danej linii na płaszczyznę współrzędnych (styczna kąta tego rzutu z osią Oz), a N jest współczynnikiem kątowym rzutu tej prostej na płaszczyznę płaszczyzna współrzędnych (styczna kąta tego rzutu z osią Oz). Liczby wyznaczają zatem kierunki rzutów danej prostej na dwie płaszczyzny współrzędnych, czyli charakteryzują także kierunek samej danej prostej. Dlatego nazywane są liczby M i N współczynniki kątowe ta linia.

Aby poznać geometryczne znaczenie stałych, postawmy w równaniach (6) linię prostą i otrzymamy: czyli punkt leży na danej prostej. Oczywiście ten punkt jest punktem przecięcia tej prostej z płaszczyzną. Są to więc współrzędne śladu tej prostej na płaszczyźnie współrzędnych

Teraz łatwo jest dokonać przejścia od równań rzutowych do równań kanonicznych. Podajmy na przykład równania (6). Rozwiązując te równania dla , znajdujemy:

z którego bezpośrednio otrzymujemy równania kanoniczne w postaci

Przykład 2. Podaj równania kanoniczne prostej

do równań w rzutach na płaszczyznę

Zapisujemy te równania w postaci

Rozwiązując pierwsze z tych równań dla x, a drugie dla y, znajdujemy wymagane równania w rzutach:

Przykład 3. Podaj równania w rzutach

do postaci kanonicznej.

Rozwiązując te równania dla , otrzymujemy.

Równania kanoniczne prostej w przestrzeni to równania definiujące linię przechodzącą przez dany punkt współliniową z wektorem kierunku.

Niech będzie dany punkt i wektor kierunkowy. Dowolny punkt leży na prostej l tylko wtedy, gdy wektory i są współliniowe, czyli jest dla nich spełniony warunek:

.

Powyższe równania są równaniami kanonicznymi prostej.

Takty muzyczne M , N I P są rzutami wektora kierunku na osie współrzędnych. Ponieważ wektor jest różny od zera, to wszystkie liczby M , N I P nie może być jednocześnie równa zeru. Ale jeden lub dwa z nich mogą okazać się zerowe. Na przykład w geometrii analitycznej dozwolony jest następujący wpis:

,

co oznacza, że ​​rzuty wektora na oś Oj I Oz są równe zeru. Dlatego zarówno wektor, jak i prosta określona równaniami kanonicznymi są prostopadłe do osi Oj I Oz, czyli samoloty yOz .

Przykład 1. Zapisz równania prostej w przestrzeni prostopadłej do płaszczyzny i przechodzący przez punkt przecięcia tej płaszczyzny z osią Oz .

Rozwiązanie. Znajdźmy punkt przecięcia tej płaszczyzny z osią Oz. Ponieważ dowolny punkt leży na osi Oz, ma zatem współrzędne , przyjmując w danym równaniu płaszczyznę x = y = 0, otrzymujemy 4 z- 8 = 0 lub z= 2 . Dlatego punkt przecięcia tej płaszczyzny z osią Oz ma współrzędne (0; 0; 2) . Ponieważ pożądana linia jest prostopadła do płaszczyzny, jest równoległa do jej wektora normalnego. Dlatego wektor kierunkowy linii prostej może być wektorem normalnym dany samolot.

Zapiszmy teraz wymagane równania prostej przechodzącej przez punkt A= (0; 0; 2) w kierunku wektora:

Równania prostej przechodzącej przez dwa dane punkty

Linię prostą można wyznaczyć przez dwa leżące na niej punkty I W tym przypadku wektorem kierującym prostej może być wektor . Wtedy równania kanoniczne prostej przyjmują postać

.

Powyższe równania wyznaczają prostą przechodzącą przez dwa dane punkty.

Przykład 2. Napisz równanie prostej w przestrzeni przechodzącej przez punkty i .

Rozwiązanie. Zapiszmy wymagane równania linii prostych w postaci podanej powyżej w podręczniku teoretycznym:

.

Ponieważ , to pożądana linia prosta jest prostopadła do osi Oj .

Prosta jak linia przecięcia płaszczyzn

Linię prostą w przestrzeni można zdefiniować jako linię przecięcia dwóch nierównoległych płaszczyzn oraz jako zbiór punktów spełniający układ dwóch równań liniowych

Równania układu nazywane są również ogólnymi równaniami linii prostej w przestrzeni.

Przykład 3. Ułóż równania kanoniczne prostej w przestrzeni podane równaniami ogólnymi

Rozwiązanie. Aby zapisać równania kanoniczne prostej, czyli równania prostej przechodzącej przez dwa dane punkty, należy znaleźć współrzędne dowolnych dwóch punktów na tej prostej. Mogą to być na przykład punkty przecięcia prostej z dowolnymi dwiema płaszczyznami współrzędnych yOz I xOz .

Punkt przecięcia prostej i płaszczyzny yOz ma odciętą X= 0 . Dlatego zakładając w tym układzie równań X= 0, otrzymujemy układ z dwiema zmiennymi:

Jej decyzja y = 2 , z= 6 razem z X= 0 definiuje punkt A(0; 2; 6) żądana linia. Następnie zakładając w zadanym układzie równań y= 0, otrzymujemy system

Jej decyzja X = -2 , z= 0 razem z y= 0 definiuje punkt B(-2; 0; 0) przecięcie prostej z płaszczyzną xOz .

Zapiszmy teraz równania prostej przechodzącej przez punkty A(0; 2; 6) i B (-2; 0; 0) :

,

lub po podzieleniu mianowników przez -2:

,

Sekcje