Wykład 4.

Ciągłość funkcji

1. Funkcja ciągłości w punkcie

Definicja 1.Pozwól funkcji y.=fA.(x.) zdefiniowany w punkcie h. 0 I w jakimś otoczeniu tego punktu. Funkcjonować y.=fA.(x.) Nazywa ciągły w pkt x 0 Jeśli w tym momencie istnieje limit funkcji i jest równa wartości funkcji w tym momencie, tj.

W porządku, stan funkcji ciągłości y.=fA.(x.) W punkcie h. 0 czy to:

Tak jak
, wówczas równość (32) można napisać jako

(33)

Oznacza to, że kiedy znalezienie limitu funkcji ciągłejfA.(x.) Możesz przejść do limitu pod znakiem funkcji, tj. w działaniu fA.(x.) Zamiast argument h. zastąpić h. 0 .

lIM SIN. x.\u003d Grzech (lim x.);

lim arctg. x.\u003d Arctg (lim x.); (34)

lIM LOG. x.\u003d LOG (LIM x.).

Zadanie.Znajdź limit: 1)
; 2)
.

Dajemy definitywność funkcji, w oparciu o koncepcję przyrostu argumentu i funkcji.

Dlatego warunki
i
To samo (rys. 4), a następnie równość (32) ma formę:

lub
.

Definicja 2. Funkcjonować y.=fA.(x.) Nazywa ciągły w pkt x 0 , Jeśli jest zdefiniowany w punkcie h. 0 I jego otoczenie, a nieskończenie niewielki przyrost argumentu odpowiada nieskończenie niewielki przyrost funkcji.

Zadanie. Przeglądaj funkcję ciągłości y.=2h. 2 1.

Właściwości funkcji, ciągły w punkcie

1. Jeśli funkcje fA.(x.) JA. φ (x.) Ciągły w punkcie h. 0, to ich kwota
, skład
i prywatny
(jeśli się uwzględni
) są funkcjami ciągłymi w punkcie h. 0 .

2. Jeśli funkcja w.=fA.(x.) ciągły w punkcie h. 0 I. fA.(x. 0)\u003e 0, wówczas jest taka dzielnica punktu h. 0, w którym. fA.(x.)>0.

3. Jeśli funkcja w.=fA.(u.) ciągły w punkcie U 0 i funkcji U \u003d φ (x.) ciągły w punkcie u 0 \u003d. φ (x. 0 ), a następnie kompleksowa funkcja y.=fA.[φ (x.)] Ciągły w punkcie h. 0 .

2. Ciągłość funkcji w przedziale i segmencie

 Funkcja y.=fA.(x.) Nazywa ciągły w przedziale (zA.; b.) Jeśli jest ciągły w każdym punkcie tego interwału.

 Funkcja y.=fA.(x.) Nazywa ciągły na cięcie [zA.; b.] Jeśli jest ciągły w przedziale ( zA.; b.) iw punktu h.=ale ciągły po prawej stronie (tj.
) i w punkcie x.=b. ciągły po lewej (tj.
).

3. Punkty funkcji pęknięcia i ich klasyfikacja

Klauzule, w których ciągłość funkcji jest zakłócana, są nazywane punkty pęknięcia Ta cecha

Jeśli h.=h. 0  punkt przerwy punkt y.=fA.(x.) Następnie nie posiada co najmniej jednego z warunków pierwszego określenia ciągłości funkcji.

Przykład.

1.
. 2.

3)
4)
.

▼ Punkt grocencji h. 0 zwany punktem przerwy pierwszy rodzaj Funkcje y.=fA.(x.) Jeśli końcowe limity funkcji po lewej i prawej stronie istnieją w tym momencie (jednostronne limity), tj.
i
. W którym:

Wielkość |. ZA. 1 -ZA. 2 |. Połączenie funkcja skoku W punkcie złamania pierwszego rodzaju. ▲.

▼ Punkt grocencji h. 0 zwany punktem przerwy drugi wyścig Funkcje y.=fA.(x.) Jeśli co najmniej jeden z jednostronnych limitów (lewy lub prawej) nie istnieje ani nie jest równy nieskończoności. ▲.

Zadanie. Znajdź punkt Gap i znajdź swój typ dla funkcji:

1)
; 2)
.

4. Główne twierdzenia dotyczące funkcji ciągłych

Kontynuuj twierdzenia o ciągłości przestrzegane są bezpośrednio z odpowiednich twierdzeń o granicach.

Twierdzenie 1. Kwota, produkt i prywatne dwie funkcje ciągłe mają ciągłą funkcję (dla prywatnego, z wyjątkiem wartości argumentu, w którym dzielnik nie jest zero).

Twierdzenie 2. Niech funkcje u.=φ (x.) ciągły w punkcie h. 0 i funkcja y.=fA.(u.) ciągły w punkcie u.=φ (x. 0 ). Następnie funkcja złożona fA.(φ (x.)), składający się z ciągłych funkcji, jest ciągły w punkcie h. 0 .

Twierdzenie 3. Jeśli funkcja y.=fA.(x.) ciągłe i ściśle monotonne na [ zA.; b.] Oś O, a następnie odwrotna funkcja w.=φ (x.) Również ciągłe i monotonne na odpowiednim segmencie [ dO.;rE.] Oś Ou.

Każda funkcja podstawowa jest ciągła w każdym punkcie, w której jest zdefiniowany.

5. Właściwości funkcji ciągły w segmencie

Twierdzenie Weierstrass. Jeśli funkcja jest ciągła w segmencie, osiągnie jego największe i najmniejsze wartości w tym segmencie.

Następstwo. Jeśli funkcja jest ciągła w segmencie, ogranicza się do segmentu.

The Bolzano Cauchy Twierdzenie.Jeśli funkcja y.=fA.(x.) ciągły w segmencie [ zA.; b.] i przyjmuje nierówne wartości na jego końcach fA.(zA.)=ZA. i fA.(b.)=B.,
Więc jaki byłby liczba Z, więzień między ALE i W,jest punkt
taka fA.(dO.)=DO..

Geometrycznie Twierdzenie jest oczywiste. Dla dowolnej liczby Zzamknięty między ALE i W, istnieje punkt z wnętrzem tego segmentu fA.(Z)=DO.. Prosto w.=Z Przejdź na wykres funkcji przynajmniej w pewnym momencie.

Następstwo. Jeśli funkcja y.=fA.(x.) ciągły w segmencie [ zA.; b.] I przyjmuje na końcu wartości różnych znaków, a następnie wewnątrz segmentu [ zA.; b.] Będzie co najmniej jeden punkt zw którym funkcja y.=fA.(x.) Adres do zera: fA.(dO.)=0.

Geometrycznyznaczenie twierdzenia: Jeśli harmonogram ciągłej funkcji porusza się po jednej stronie osi O do drugiego, przechodzi do osi O.

Funkcja ciągłości w punkcie

Przypuśćmy, że funkcja F (X) jest zdefiniowana w niektórych momentach O (X0) X0 (w tym sama X0).

Funkcja F (x) nazywa się ciągłą w punkcie X0, jeśli występuje Limx → X0 F (X) równa wartości funkcji F (X) w tym momencie: LIM

f (x) \u003d f (x0), (1)

te. "O (f (x0)) $ O (x0): x o (x0) ya f (x) o (f (x0)).

Komentarz. Równość (1) można zapisać w formie: LIM

te. Pod znakiem funkcji ciągłej można przejść do limitu.

Niech Δx \u003d X - X0 będzie przyrostem argumentu, Δy \u003d f (x) - f (x0) - odpowiednie przyrost funkcji.

JA. wystarczający stan Funkcja ciągłości w punkcie

Funkcja Y \u003d F (X) jest ciągły w punkcie X0, jeśli i tylko wtedy, gdy

Komentarz. Warunek (2) można interpretować jako drugą definicję funkcji ostatecznej w punkcie. Obie definicje są równoważne.

Niech funkcja F (X) zostanie zdefiniowana w półprzestępnym.

Funkcja F (X) nazywana jest ciągłym lewo w punkcie X0, jeśli jest limit jednokierunkowy

Ciągłość kwoty, prac i prywatnych dwóch funkcji ciągłych

Twierdzenie 1. Jeśli funkcje f (x) i g (x) są ciągłe w punkcie x0, w tym momencie są ciągłe f (x) ± g (x), f (x) · g (x), f ( x)

Ciągłość kompleksowej funkcji

Twierdzenie 2. Jeśli funkcja U (X) jest ciągła w punkcie X0, a funkcja F (U) jest ciągła w odpowiednim punkcie U0 \u003d F (x0), a następnie kompleksową funkcję F (U (X)) jest ciągły w pkt x0.

Wszystkie podstawowe funkcje są ciągłe w każdym punkcie ich obszarów definicji.

Lokalne właściwości funkcji ciągłych

Twierdzenie 3 (ograniczona funkcja ciągła). Jeśli funkcja F (X) jest ciągła w punkcie X0, znajduje się sąsiedztwo o (x0), w którym f (x) jest ograniczone.

Dowód wynika z zgody ograniczonej funkcji mającym limit.

Twierdzenie 4 (stabilność znaku ciągłej funkcji). Jeśli funkcja f (x) jest ciągła w pkt x0 i f (x0) ≠ 0, wówczas jest sąsiedztwo punktu x0, w którym f (x) ≠ 0, a znak f (x) w tym obszarze zbiega się Znak f (x0) w tym sąsiedztwie.

Klasyfikacja punktów pęknięcia

Warunek (1) ciągłości funkcji F (X) w punkcie X0 jest równoważny warunkom F (X0 - 0) \u003d F (X0 + 0) \u003d F (x0), (3)

gdzie f (x 0 - 0) \u003d lim

f (x) i f (x0 + 0) \u003d lim

f (x) - jednostronne limity funkcji F (x) w punkcie x0.

Jeśli warunek (3) zostanie naruszony, punkt x0 nazywa się punktem pęknięcia f (x). W zależności od rodzaju naruszenia warunku (3) punkty pęknięcia są różne i są klasyfikowane w następujący sposób:

1. Jeśli w punkcie X0 istnieje jednostronne limity f (x0 - 0), f (x0 + 0) i

f (x0 - 0) \u003d f (x0 + 0) ≠ f (x0), a następnie punkt x0 nazywany jest wyjmowanym punktem przerwania f (x) (rys. 1).

Komentarz. W punkcie X0 funkcja może nie zostać zdefiniowana.

2. Jeśli w punkcie X0 istnieje jednostronne limity f (x0 - 0), f (x0 + 0) i

f (x0 - 0) ≠ F (x0 + 0), a następnie punkt X0 nazywa się punktem przerwowym z faktem Funkcją skoku F (X) (rys. 2).

Komentarz. W punkcie przerwy z końcowym skokiem, wartość funkcji może być dowolna, i nie może być określona.

Jednorazowe punkty przerwania i skok końcowy nazywane są kropkami odstępu pierwszego rodzaju. Im osobliwość jest istnieniem skończonych jednostronnych limitów f (x0 - 0) i

3. Jeśli w punkcie x0 co najmniej jeden z jednostronnych limitów f (x0 - 0), f (x0 + 0) jest równy nieskończoności lub nie istnieje
x0 nazywa się punktem zwrotu drugiego rodzaju (rys. 3).

Jeśli co najmniej jeden z jednostronnych limitów f (x0 - 0), f (x0 + 0) jest nieskończoności, a następnie proste x \u003d x 0 nazywa się pionową asymptota funkcji funkcji Y \u003d f (x) .

Definicja. Funkcja F (x), określona w sąsiedztwie określonego punktu X0, nazywana jest ciągła w punkcie X0, jeśli limit funkcji i jej wartość w tym punkcie jest równa, tj.

Ten sam fakt może być zapisany w inny sposób:

Definicja. Jeśli funkcja F (X) jest zdefiniowana w określonym sąsiedztwie punktu x0, ale nie jest ciągły w samym punkcie X0, nazywa się to funkcją nieciągłą, a punkt X0 jest punktem szczeliny.

Definicja. Funkcja F (x) nazywa się ciągłą w punkcie X0, jeśli dla każdego liczba dodatnia E\u003e 0 Jest taka liczba D\u003e 0, która dla każdego X spełniająca stan

prawdziwa nierówność.

Definicja. Funkcja F (x) nazywa się ciągłą w punkcie X \u003d X0, jeśli przyrost funkcji w punkcie X0 jest nieskończenie małą wartością.

f (x) \u003d f (x0) + a (x)

gdzie A (X) jest nieskończenie mały w X®x0.

Właściwości funkcji ciągłych.

1) Kwota, różnica i produkt funkcji są ciągły w punkcie X0 - istnieje funkcja ciągła w pkt x0.

2) Prywatne dwie funkcje ciągłe - istnieje ciągła funkcja, pod warunkiem, że g (x) nie jest zero w punkcie x0.

3) Superpozycja funkcji ciągłych - istnieje ciągła funkcja.

Ta właściwość może być rejestrowana w następujący sposób:

Jeśli u \u003d f (x), v \u003d g (x) - funkcje ciągłe w punkcie x \u003d x0, a następnie funkcja V \u003d g (f (x)) jest również ciągłą funkcją w tym momencie.

Ważność powyższych właściwości można łatwo udowodnić za pomocą twierdzeń granicznych

Właściwości funkcji ciągły w segmencie.

Nieruchomość 1: (The First Weierstrass Twierdzenie (Weierstrass Karl (1815-1897) jest niemieckim matematykiem)). Funkcja ciągła w segmencie jest ograniczona w tym segmencie, tj. Segment jest wykonywany przez warunek -M f (x) £ M.

Dowód tej właściwości opiera się na fakcie, że funkcja jest ciągła w punkcie X0 jest ograniczona w niektórych okolicach, a jeśli podzielisz segment do nieskończonej liczby segmentów, które są "dokręcone" do punktu X0, powstaje niektóre sąsiedztwo punktu X0.

Nieruchomość 2: Funkcja ciągła w segmencie trwa go największe i najmniejsze wartości.

Te. Istnieją takie wartości x1 i x2, że f (x1) \u003d m, f (x2) \u003d m, i

Należy pamiętać, że te największe i najmniejsze wartości funkcji mogą przyjąć segment i kilka razy (na przykład - F (x) \u003d Sinx).

Różnica między największymi i najniższymi wartościami funkcji w segmencie nazywana jest oscylacją funkcji w segmencie.

Nieruchomość 3: (drugi teore bolzano - Cauchy). Funkcja ciągła w segmencie nabiera tego segmentu wszystkie wartości między dwiema dowolnymi wartościami.

Nieruchomość 4: Jeśli funkcja f (x) jest ciągła w punkcie x \u003d x0, istnieje pewne sąsiedztwo punktu x0, w którym funkcja zapisuje znak.

Nieruchomość 5: (Twierdzenie Bolzano (1781-1848) - Cauchy). Jeśli funkcja F (X) jest ciągła w segmencie i ma na końcach segmentu Wartości przeciwnych znaków, istnieje taki punkt w tym segmencie, gdzie f (x) \u003d 0.

Te. Jeśli znak (f (a)) ¹ znak (f (b)), a następnie X0 $: F (x0) \u003d 0.

Definicja. Funkcja F (X) nazywana jest jednolicie ciągła w segmencie, jeśli istnieje D\u003e 0 dla dowolnego E\u003e 0, że dla dowolnych punktów X1î i X2î

ïx2 - x1ï.< D

prawdziwe nierówności ïf (x2) - f (x1) ï< e

Różnica między jednolitą ciągłością z "zwykłego" jest to, że dla każdej e jest jego D, niezależnie od X, oraz z "normalną" ciągłością D zależy od E i X.

Nieruchomość 6: Twierdzenie Cantora (Kantor George (1845-1918) jest niemieckim matematykiem). Funkcja ciągła w segmencie jest równomiernie ciągła.

(Ta właściwość jest ważna tylko dla segmentów, a nie dla interwałów i półokręgów).

Definicja ciągłości

Funkcja F (X) nazywa się ciągłą w punkcie A, jeśli: w F () PP

1) Funkcja F (X) jest zdefiniowana w punkcie A,

2) ma skończony limit w X → A 2) ma końcowy limit w X → A,

3) Ten limit jest równy wartości funkcji w tym momencie:

Ciągłość w przedziale

Funkcja F (X) nazywa się ciągłą w przedziale X, jeśli F () RR RR

Jest ciągły w każdym punkcie tej luki.

Komunikat. Funkcje allologiczne są ciągłe

Obszary ich definicji.

Ograniczona funkcja (ograniczona funkcja)

Funkcjonowała ograniczona obsługa, jeśli

otrzymywaniem M jest to, że dla "X ∈ jest wykonywane

nierówność: |. F (x) | ≤ M.

Dwie teoremy weierstrass.

Themetoremäviersstrass.. Jeśli funkcja F (X p Prol F F (

ciągły nadzór, Tonaogrichenanaeetomotrech

Nadrukujący. Jeśli funkcja f (x

ciągła niespodzianka, Tunika Tuniter Butomotrus

najmniejsze banery M M. Inaganly Signefications

Bolzano Cauchy Twierdzenie

Jeśli funkcja f (x) nieustannie zaskoczona fu f () pp r

koniec cięcia F (A) i F (b) są skonfrontowane,

tovnotriotre cięcia C∈ (A, B) tak, że F (C) \u003d 0. Ur P () F ()

Funkcja ciągłości. Punkt pęknięcia.

Jest byk, kołysanie, westchnienia w podróży:
- Och, zarząd się kończy, teraz upadnę!

W tej lekcji przeanalizujemy koncepcję ciągłości funkcji, klasyfikacja punktów szczelinowych i wspólnego zadania praktycznego funkcje badawcze do ciągłości. Z samej nazwy tematu wiele intuicyjnie zdaje sobie sprawę, co zostanie wydane i pomyśleć, że materiał jest dość prosty. To prawda. Ale to dokładnie proste zadania najczęściej karane za lekceważenie i powierzchowne podejście do ich rozwiązania. Dlatego polecam bardzo ostrożnie studiować artykuł i złapać wszystkie subtelności i techniki techniczne.

Co musisz wiedzieć i być w stanie?Naprawdę dużo. Aby uzyskać lekcję o wysokiej jakości, konieczne jest zrozumienie, co jest limit funkcji. . Niski czytniki przygotowawcze są wystarczające do zrozumienia artykułu Limity funkcji. Przykłady rozwiązań i patrzeć znaczenie geometryczne. limit w metodach Wykresy i właściwości funkcji podstawowych . Wskazane jest również zapoznanie się z przekształcenia wykresu geometrycznego Od czasu praktyki w większości przypadków obejmuje budowanie rysunku. Perspektywy są optymistyczne dla każdego, a nawet kompletny czajnik będzie w stanie niezależnie poradzić sobie z zadaniem w następnej godzinie - inne!

Funkcja ciągłości. Riptenty i ich klasyfikacja

Koncepcja funkcji ciągłości

Rozważaj pewną funkcję, ciągłe na całej linii numerycznej:

Lub, mówiąc bardziej zwięzły, nasza funkcja jest ciągła włączona (wiele liczb).

Co to jest kryterium ciągłości "Filistynu"? Oczywiście można wyciągnąć wykres funkcji ciągłej bez robienia ołówka z papieru.

Jednocześnie należy wyraźnie wyróżnić dwie proste koncepcje: obszar definicji funkcji. i funkcja ciągłości. Ogólnie to nie to samo. Na przykład:

Ta cecha określony na całym numerycznym prostym, dla kAŻDY Znaczenia "X" istnieją swoje znaczenie "Gry". W szczególności, jeśli to. Należy pamiętać, że kolejny punkt ludności, ponieważ z definicji funkcji, wartość argumentu musi odpowiadać jedyną rzeczą Wartość funkcji. W ten sposób, domena Nasza funkcja :.

ale ta funkcja nie jest ciągła! Oczywiście w momencie toleruje złamać. Termin jest również dość zrozumiały i odwiedzany, rzeczywiście, ołówek tutaj dla każdego będzie musiał oderwać papier. Nieco później rozważymy klasyfikację punktów szczelin.

Ciągłość funkcji w punkcie i w przedziale

W taki czy inny sposób zadanie matematyczne Możemy porozmawiać o ciągłości funkcji w punkcie, ciągłości funkcji w przedziale, pół-przedziale lub ciągłości funkcji w segmencie. To znaczy, nie ma "ciągłości" - Funkcja może być gdzieś ciągła. I fundamentalna "cegła" wszystkiego innego funkcja ciągłości w punkcie .

Teoria analiza matematyczna Daje determinację ciągłości funkcji w punkcie za pomocą delty i epsilonu otoczenia, ale w praktyce istnieje kolejna definicja, do kogo będziemy zwracać szczególną uwagę.

Najpierw pamiętaj jednostronne limityKto wpadł w nasze życie w pierwszej lekcji o wykresach funkcji . Rozważ w ciągu tygodnia:

Jeśli podejdziesz do osi do punktu lewo (Red strzałka), a następnie odpowiednie wartości "Igarek" pójdą wzdłuż osi do punktu (strzałka malinowa). Matematycznie ten fakt jest ustalony limit lewostronny:

Zwróć uwagę na wpis (Iks czytają po lewej stronie "). "Dodatek" "minus zero" symbolizuje W rzeczywistości oznacza to, że zbliżamy się z lewej strony.

Podobnie, jeśli zbliża się do punktu "ka" po prawej (niebieska strzałka), a następnie "zapłon" przyjdzie do tego samego znaczenia, ale już na zielonej strzałce i limit słupkowy będzie następujący:

"Dodatek" symbolizuje A nagranie jest tak czytane: "X dąży do właściwego".

Jeśli jednostronne limity są skończone i równe (jak w naszym przypadku): , powiemy, że jest wspólny limit. Wszystko jest proste, ogólny limit jest naszym "zwykłym" limit funkcji. równa skończonej liczbie.

Należy pamiętać, że jeśli funkcja nie jest zdefiniowana w (wypełnij czarny punkt na gałęzi tablicy), a następnie wymienione obliczenia pozostają ważne. Jak wielokrotnie odnotowałem, w szczególności w artykule o nieskończenie małych funkcjach , Wyrażenia oznaczają, że "X" nieskończenie blisko zbliża się do punktu w tym samym czasie NIEISTOTNYSama funkcja jest określona w tym momencie lub nie. Dobry przykład zostanie spełniony w następnym akapicie, gdy funkcja jest analizowana.

Definicja: Funkcja jest ciągła w punkcie, jeśli limit funkcji w tym momencie jest równa wartości funkcji w tym momencie :.

Definicja jest opisana w następujących warunkach:

1) Funkcja musi być zdefiniowana w punkcie, czyli, musi istnieć wartość.

2) Musi istnieć wspólny limit funkcji. Jak wspomniano powyżej, oznacza to istnienie i równość ograniczeń jednokierunkowych: .

3) Limit funkcji w tym punkcie powinien być równy wartości funkcji w tym momencie :.

Jeśli naruszono przynajmniej jeden W trzech warunkach funkcja traci własność ciągłości w punkcie.

Funkcja ciągłości w przedziale Formułuj dowcipny i bardzo prosty: funkcja jest ciągła w przedziale, jeśli jest ciągły w każdym punkcie tego interwału.

W szczególności wiele funkcji jest ciągły na nieskończonym przedziale, czyli na różnych ważnych liczbach. Jest to funkcja liniowa, wielomian, wykładnik, zatok, cosinus itp. W ogóle, każdy funkcja podstawowa Ciągły na moim obszary definicji Na przykład funkcja logarytmiczna jest ciągła w przedziale. Mam nadzieję, że K. ten moment Wyobrażasz sobie całkiem dobrze, jak wygląda grafika podstawowych funkcji. Jeszcze dokładna informacja o ich ciągłości można się nauczyć dobry człowiek Przez nazwę FIHtendholz.

Wraz z ciągłością funkcji w segmencie i pół-przedziałach wszystko jest również proste, ale bardziej należy powiedzieć w lekcji o znalezieniu minimalnych i maksymalnych wartości funkcji w segmencie , W międzyczasie nie młodzi nas głowy.

Klasyfikacja punktów pęknięcia

Fascynującym życiem funkcji jest bogaty we wszelkiego rodzaju specjalne punkty, a punkty luk są tylko jedną z stron swojej biografii.

Uwaga : Na wypadek, gdyby skupić się na podstawowej chwili: Punkt Gap jest zawsze oddzielony punkt - Nie ma "kilku punktów zerwania w rzędzie", to znaczy, nie ma czegoś takiego jak "przerwę".

Te punkty z kolei są podzielone na dwie duże grupy: pierwszy rodzaj luk i rale drugiego rodzaju. Każdy rodzaj luki ma swój własny charakterystykaktóre teraz patrzymy teraz:

Punkt przerwania pierwszego rodzaju

Jeśli stan ciągłości jest uszkodzony w punkcie i jednostronne limity drobniejszy Wtedy nazywa się punkt łamania pierwszego rodzaju.

Zacznijmy od najbardziej optymistycznego przypadku. Po wstępnym pomysłem lekcji chciałem powiedzieć teorii " generał"Ale aby zademonstrować rzeczywistość materiału, zatrzymał się w wariancie z określonymi podmiotami.

Zdjęcie nowożeńców jest smutne na tle wiecznego płomienia, ale następna ramka jest ogólnie akceptowana. Zdjęcia w funkcji harmonogramu rysunku:


Ta funkcja jest ciągła na całym numerycznym bezpośrednim, z wyjątkiem punktu. W rzeczywistości mianownik nie może być zero. Jednak zgodnie ze znaczeniem limitu - możemy nieskończenie blisko Podejdź do "zera", a po lewej i prawej, to znaczy, że istnieją jednostronne limity i, oczywiście, zbiegają się:
(Stan ciągłości jest zakończony).

Ale funkcja nie jest zdefiniowana w tym momencie, dlatego ciągłość 1 stan zostanie naruszony, a funkcja jest ciągnięta w tym momencie.

Łamanie takiego rodzaju (z istniejącymi wspólny limit) Połączenie rozporządzalny pęknięcie. Dlaczego wyeliminowany? Ponieważ funkcja może dolegliwość W punkcie przerwy:

Wygląda dziwnie? Może. Ale taki zapis funkcji nic nie zaprzecza! Teraz luka jest wyeliminowana i wszyscy są szczęśliwi:


Wykonaj formalny czek:

2) - istnieje ogólny limit;
3)

Zatem wszystkie trzy warunki są wykonane, a funkcja jest ciągła w punkcie, aby określić ciągłość funkcji w punkcie.

Jednakże nienawiści Matana mogą mieć wpływ na funkcję ze złym sposobem, na przykład :


Jest ciekawy, że wykonano tutaj pierwsze dwa warunki ciągłości:
1) - Funkcja jest określona w tym momencie;
2) - Ogólny limit istnieje.

Ale trzeci frontier nie jest podróżowany: w punkcie jest funkcja limitu nie równe Wartość tej funkcji w tym momencie.

Tak więc w punkcie funkcja cierpi na przerwę.

Po drugie, nazywa się bardziej smutny przypadek zgraj pierwszy rodzaj ze skokiem. A smutek wywołany jednostronne ograniczenia skończony i inny. Przykład jest przedstawiony na drugim rysowaniu lekcji. Taka luka występuje, z reguły, w fragmentaryczne funkcje określonektóre już zostały wymienione w artykule na przemianach wykresów. .

Rozważ funkcję utworu I wykonaj jego rysunek. Jak zbudować wykres? Bardzo prosta. W półpokojowym fragmencie paraboli ( zielony kolor), w przedziale - wyciąć prosto (czerwony) i na pół-interwał - bezpośredni (niebieski kolor).

Jednocześnie, ze względu na nierówność, wartość jest zdefiniowana funkcja kwadratowa (Zielony punkt), a na mocy nierówności wartość jest zdefiniowana dla funkcji liniowej (niebieska kropka):

W bardzo trudnym przypadku sprawa powinna być uciekana do bieżącej konstrukcji każdej grafiki (patrz pierwszy lekcja na wykresach funkcji ).

Teraz będziemy zainteresowani tylko punktem. Przeglądaj go do ciągłości:

2) Oblicz jednostronne limity.

Po lewej stronie mamy czerwoną linię cięcia, więc limit lewostronny:

Prawo - niebieski, prosty i prawowy granica:

W rezultacie uzyskany ostateczne numery, i oni nie równe. Ponieważ ograniczenia jednokierunkowe skończony i inny: , a następnie nasza funkcja toleruje gap pierwszego rodzaju z skokiem.

Logiczne jest, że luka nie jest wyeliminowana - funkcja nie jest tego nie robić, a "nie klej", jak w poprzednim przykładzie.

Punkty złamania drugiego rodzaju

Zazwyczaj ta kategoria spryt obejmuje wszystkie inne przypadki pęknięcia. Nie wymieniam wszystkiego, ponieważ w praktyce na 99% odsetki zadań spotkają się z tobą nieskończona przerwa - gdy pozostawione lub słuszne, a częściej oba limity są nieskończone.

I oczywiście najbardziej odpowiedni obraz - hiperbolia w punkcie zero. Tutaj obie jednostronne limit są nieograniczone: Dlatego funkcja toleruje szczelinę drugiego sortowania w punkcie.

Staram się wypełnić moje artykuły z najbardziej zróżnicowanymi treściami, więc spójrzmy na harmonogram funkcji, który jeszcze nie spotkał:

Według standardowego schematu:

1) Funkcja nie jest określona w tym momencie, ponieważ mianownik odnosi się do zera.

Oczywiście można natychmiast stwierdzić, że funkcja cierpi na szczelinę w miejscu, ale dobrze byłoby sklasyfikować naturę luki, co jest często wymagane przez stan. Dla tego:

Przypominam, że pod rekordem jest rozumiany nieskończenie mały numer ujemnyi pod rekordem - nieskończenie niewielka liczba dodatnia.

Limity jednokierunkowe są nieskończone, oznacza to, że funkcja cierpi na szczelinę 2nd rodu w punkcie. Oś rzędna jest pionowa asmeptota. Za harmonogram.

Sytuacja nie jest rzadka, gdy istnieją obie jednostronne limity, ale tylko jeden z nich jest nieograniczony, na przykład:

Jest to wykres funkcji.

Przeglądaj punkt ciągłości:

1) Funkcja nie jest określona w tym momencie.

2) Oblicz limity jednokierunkowe: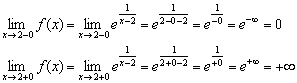

Porozmawiamy o metodzie obliczania takich jednostronnych limitów w dwóch ostatnich przykładach wykładu, chociaż wielu czytelników już widział i domyślił.

Limit lewostronny jest skończony i równy zero (w punkcie "nie idziemy"), ale limit prawą jest nieskończenie, a pomarańczowy oddział wykresu jest nieskończenie blisko jego pionowa asymptota określone przez równanie (czarny kropkowany).

Zatem funkcja toleruje luka drugiego rodzaju W punkcie.

Jeśli chodzi o szczelinę pierwszego rodzaju, w punkcie punktu przerwania można określić funkcję. Na przykład, dla funkcji utworu Odważnie umieść czarny pogrubiony punkt na początku współrzędnych. Po prawej - gałęzi hiperboli, a limit prawą jest nieskończony. Myślę, że prawie wszystkie przedstawione, jak wygląda ten harmonogram.

Co czekali na:

Jak zbadać funkcję ciągłości?

Badanie funkcji ciągłości w punkcie odbywa się na już schematu rutynowym, który ma weryfikację trzech warunków ciągłości:

Przykład 1.

Przeglądaj funkcję

Decyzja:

1) Pod oczami jest jedynym punktem, w którym funkcja nie jest zdefiniowana.

2) Oblicz limity jednokierunkowe:

Jednostronne limity są skończone i równe.

Tak więc w punkcie funkcja cierpi na jednorazową szczelinę.

Jak wygląda wykres tej funkcji?

Chcę być uproszczony i wydaje się być zwykłą parabola. ALE Początkowa funkcja nie jest zdefiniowana w punkcie, więc wymagana jest następująca rezerwacja:

Wykonaj rysunek:

Odpowiedź: Funkcja jest ciągła na całym numerycznym bezpośrednio, z wyjątkiem punktu, w którym jest ciągnięta przez jednorazową szczelinę.

Funkcja może być wykonana dobra lub nie w taki sposób, ale pod warunkiem nie jest to wymagane.

Czy mówisz wyjątkowy przykład? Ani trochę. Dziesiątki czasów spotkały się w praktyce. Prawie wszystkie zadania strony pochodzą z prawdziwych prac niezależnych i testowych.

Jesteśmy podzielone na swoje ulubione moduły:

Przykład 2.

Przeglądaj funkcję Na ciągłość. Określ naturę przerw w funkcji, jeśli istnieją. Wykonaj rysunek.

Decyzja: Z jakiegoś powodu uczniowie boją się i nie lubią funkcji z modułem, chociaż nic się w nich nie skomplikowane. W lekcji dotknęliśmy takich rzeczy. Przekształcenia wykresu geometrycznego . Ponieważ moduł nie jest negatywny, ujawnia się w następujący sposób: gdzie "Alpha" jest niektóre wyrażenie. W takim przypadku nasza funkcja powinna podpisać fragmentaryczny sposób:

Ale frakcje obu kawałków muszą zostać zmniejszone przez. Redukcja, jak w poprzednim przykładzie nie przejdzie bez konsekwencji. Początkowa funkcja nie jest zdefiniowana w punkcie, ponieważ mianownik dodaje do zera. Dlatego system powinien dodatkowo określić warunek, a pierwsza nierówność powinna być surowa:

Teraz o bardzo przydatnej decyzji o decyzji.: Przed zakończeniem zadanie w projekcie jest opłacalne, aby zrobić rysunek (niezależnie od tego, czy jest to wymagane przez warunek, czy nie). Pomoże to, najpierw natychmiast patrz punkty ciągłości i punktu szczelin, a po drugie, w 100% zaoszczędzi przed błędami podczas znalezienia jednostronnych limitów.

Wykonaj rysunek. Zgodnie z naszymi obliczeniami, po lewej stronie punktu, konieczne jest narysowanie fragmentu parabola (niebieskiego), a po prawej stronie - kawałek paraboli (czerwony), a funkcja nie jest zdefiniowana w samym punkcie:

Jeśli są wątpliwości, wykonaj kilka wartości "x", zastąpić je do funkcji (Nie zapominając, że moduł niszczy ewentualny znak "minus") i sprawdź harmonogram.

Badamy funkcję ciągłości analitycznie:

1) Funkcja nie jest zdefiniowana w punkcie, dzięki czemu można natychmiast powiedzieć, że nie jest w nim ciągły.

2) Ustal naturę luki, w tym obliczymy limity jednokierunkowe:

Limity jednokierunkowe są skończone i różne, oznacza to, że funkcja toleruje różnicę pierwszego rodzaju z skokiem w punkcie. Po raz kolejny zauważ, że gdy znajdziesz limity, nie ma znaczenia, funkcja jest zdefiniowana w punkcie przerwy, czy nie.

Teraz pozostaje przemieszczać rysunek z projektu (jest wykonany tak, jakby korzystać z badania ;-)) i wypełnij zadanie:

Odpowiedź: Funkcja jest ciągła na całym numerycznym bezpośrednio, z wyjątkiem punktu, w którym toleruje pierwszy rodzaj przerwy z skokiem.

Czasami musisz dodatkowo określić wyciek. Jest obliczany jest to elementarne - od prawego limitu należy odliczyć lewy limit:, to jest, w punkcie przerwy, nasza funkcja podskoczyła przez 2 jednostki w dół (jak mówimy znak "minus").

Przykład 3.

Przeglądaj funkcję Na ciągłość. Określ naturę przerw w funkcji, jeśli istnieją. Zrobić remis.

Jest to przykład dla niezależnego rozwiązania, przykładowego roztworu próbkowania na końcu lekcji.

Odwróćmy się do najbardziej popularnej i wspólnej wersji zadania, gdy funkcja składa się z trzech części:

Przykład 4.

Przeglądaj funkcję ciągłości i zbuduj wykres funkcji .

Decyzja: Oczywiście wszystkie trzy części funkcji są ciągłe w odpowiednich odstępach czasu, więc pozostaje do sprawdzenia tylko dwóch punktów "połączenie" między kawałkami. Po pierwsze, wykonam rysunek na temat projektu, techniki budowy, narzekłem szczegółowo w pierwszej części artykułu. Jedynym, konieczne jest, aby dokładnie prześledzić nasze specjalne punkty: Ze względu na nierówność, wartość należy do linii prostej (zielony punkt) oraz na mocy nierówności, wartość należy do paraboli (Red Dot):


Cóż, zasadniczo wszystko jest jasne \u003d) pozostaje decyzję. Dla każdego z dwóch punktów "Butt" w standardowej 3 warunkach ciągłości:

JA) Przeglądaj punkt ciągłości

1)

Limity jednokierunkowe są skończone i różne, oznacza to, że funkcja toleruje różnicę pierwszego rodzaju z skokiem w punkcie.

Oblicz szczelinę skok jako różnicę między limitami prawami a lewicami:
Oznacza to, że harmonogram rzucił się do jednej jednostki w górę.

II) Przeglądaj punkt ciągłości

1) - Funkcja jest zdefiniowana w tym momencie.

2) Znajdziemy limity jednokierunkowe:

- Jednostronne limity są skończone i równe, co oznacza, że \u200b\u200bistnieje ogólny limit.

3) - Funkcja limitu w punkcie jest równa wartości tej funkcji w tym momencie.

Na ostatnim etapie przenosimy rysunek do pierwszego Chistika, po czym umieściliśmy ostateczny akord:

Odpowiedź: Funkcja jest ciągła na całym numerycznym bezpośrednim, z wyjątkiem punktu, w którym toleruje pierwszy rodzaj przerwy z skokiem.

Przykład 5.

Przeglądaj ciągłość i buduj jego harmonogram .

Jest to przykład dla niezależnego rozwiązania, krótkiego rozwiązania i przykładowej próbki projektu zadań na końcu lekcji.

Może to być wrażenie, że w pewnym momencie funkcja musi koniecznie być ciągła, a druga - musi być luka. W praktyce nie zawsze jest tak. Staraj się nie zaniedbywać pozostałych przykładów - będzie kilka interesujących i ważnych żetonów:

Przykład 6.

Funkcja Dana. . Przeglądaj funkcję ciągłości w punktach. Zbuduj wykres.

Decyzja: I znowu natychmiast wykonam rysunek w projekcie:

Cechą tego harmonogramu jest to, że z funkcją ustawiono równanie osi odcięcia. Tutaj ta działka jest narysowana przez zieleń, aw notebooku jest zwykle wybucha w tłustym prosty ołówek. I oczywiście nie zapominaj o naszych ramach: Wartość odnosi się do gałęzi stycznej (czerwona kropka), a wartość należy do linii.

Od rysunku wszystko jest jasne - funkcja jest ciągła na całym numerycznym bezpośrednim, pozostaje roztwór, który jest sprowadzany do pełnego automatyzmu dosłownie po 3-4 podobnych przykładach:

JA) Przeglądaj punkt ciągłości

1) - Funkcja jest określona w tym momencie.

2) Oblicz limity jednokierunkowe:

Więc istnieje ogólny limit.

Trygentny fakt przypomni Ci jakikolwiek strażak: stały limit jest równy ciągłym stałym. W tym przypadku limit zerowy wynosi sam zero (limit lewostronny).

3) - Funkcja limitu w punkcie jest równa wartości tej funkcji w tym momencie.

W ten sposób funkcja jest ciągła w punkcie, aby określić ciągłość funkcji w punkcie.

II) Przeglądaj punkt ciągłości

1) - Funkcja jest określona w tym momencie.

2) Znajdziemy limity jednokierunkowe:

I tutaj - limit jednostkowy jest równy samej jedności.

- Ogólny limit istnieje.

3) - Funkcja limitu w punkcie jest równa wartości tej funkcji w tym momencie.

W ten sposób funkcja jest ciągła w punkcie, aby określić ciągłość funkcji w punkcie.

Jak zwykle, po badaniu przenosimy nasz rysunek do Cleanstik.

Odpowiedź: Funkcja jest ciągła w punktach.

Należy pamiętać, że w stanie nie pytaliśmy niczego o badanie całej funkcji ciągłości, a dobry ton matematyczny jest uważany za formułowany dokładny i wyraźny Odpowiedź na kwestionowane pytanie. Nawiasem mówiąc, jeśli pod warunkiem nie jest zobowiązany do zbudowania harmonogramu, a następnie masz pełne prawo do tego, a nie budować (jednak nauczyciel może to zrobić).

Małe matematyczne "Patter" na niezależne rozwiązanie:

Przykład 7.

Funkcja Dana. . Przeglądaj funkcję ciągłości w punktach. Sklasyfikuj punkty luki, jeśli są. Wykonaj rysunek.

Spróbuj "odpowiadać" wszystkie "słowa" \u003d), a harmonogram, aby narysować bardziej precyzyjną, dokładność, nie będzie zbyt wiele ;-)

Jak pamiętasz, poleciłem natychmiast rysować rysunek na projekcie, ale od czasu do czasu są takie przykłady, gdzie nie zrozumiesz, jak wygląda harmonogram. Dlatego w niektórych przypadkach korzystne jest najpierw znaleźć jednostronne limity i tylko wtedy na podstawie badania, przedstawiające gałęzie. W dwóch ostatnich przykładach, dodatkowo opanujemy technikę obliczania niektórych jednostronnych limitów:

Przykład 8.

Zbadaj funkcję ciągłości i zbuduj jego schematyczny wykres.

Decyzja: Złe punkty są oczywiste: (rysuje mianownik wskaźnika do zera) i (rysuje denomoter całej frakcji do zera). Nie jest możliwe, jak wygląda harmonogram tej funkcji, a zatem lepiej jest prowadzić badanie.

Definicja. Funkcja F (X), określona w sąsiedztwie pewnego punktu x 0, nazywa się ciągły w pktx 0, jeśli limit funkcji i jego wartość w tym punkcie jest równa, tj.

Ten sam fakt może być zapisany w inny sposób:

Definicja. Jeśli funkcja f (X) jest zdefiniowana w niektórych sąsiedztwie punktu x 0, ale nie jest ciągły w punkcie X 0, to jest nazywany wybuchający Funkcja i punkt x 0 - punkt Gap.

Przykład funkcji ciągłej:

y.

0 x 0 - x 0 x 0 +  x

P. rymerowa funkcja nieciągła:

Definicja. Funkcja F (X) nazywa się ciągłą w punkcie X 0, jeśli występuje taka liczba \u003e 0 dla dowolnej pozytywnej liczby \u003e 0, która dla każdego x spełniająca warunek

prawdziwa nierówność
.

Definicja. Funkcja F (X) jest nazywana ciągły W punkcie x \u003d x 0, jeśli przyrost funkcji w punkcie X 0 jest nieskończenie małą wartością.

f (x) \u003d f (x 0) +  (x)

gdzie  (x) jest nieskończenie mały z XX 0.

Właściwości funkcji ciągłych.

1) Suma, różnica i produkt funkcji Ciągły w punkcie X 0 - W punkcie X 0 jest funkcja ciągła.

2) Prywatne dwie funkcje ciągłe - Jest funkcja ciągła, pod warunkiem, że g (x) nie jest zero w punkcie x 0.

3) Superpozycja funkcji ciągłych - istnieje ciągła funkcja.

Ta właściwość może być rejestrowana w następujący sposób:

Jeśli u \u003d f (x), V \u003d g (x) są funkcjami ciągłymi w punkcie x \u003d x 0, a następnie funkcja V \u003d g (f (x)) jest również ciągłą funkcją w tym momencie.

Ważność powyższych właściwości można łatwo udowodnić za pomocą twierdzeń granicznych.

Ciągłość niektórych funkcji podstawowych.

1) Funkcja F (X) \u003d C, C \u003d Const - Ciągła funkcja na całej okolicy definicji.

2) Rational Funkcja
ciągły dla wszystkich wartości x, z wyjątkiem tych, w których adresy mianownik do zera. Zatem funkcja tego gatunku jest ciągła w całej powierzchni definicji.

3) Funkcje trygonometryczne Sincosneprers w ich dziedzinie definicji.

Udowadniamy nieruchomość 3 dla funkcji Y \u003d Sinx.

Piszemy przyrost funkcji y \u003d sin (X + x) - Sinx lub po konwersji:

Rzeczywiście, istnieje limit pracy dwóch funkcji.
i
. Jednocześnie funkcja Cosinus jest ograniczoną funkcją opcji
, i to

limit funkcji zatok
, to jest nieskończenie mały.

W związku z tym istnieje produkt ograniczonej funkcji w nieskończenie małym, dlatego jest to produkt, tj. Funkcja u - nieskończenie mały. Zgodnie z opisami omówionymi powyżej, funkcja Y \u003d Sinx jest ciągłą funkcją dla dowolnej wartości x \u003d x 0 z obszaru definicji, ponieważ Jej przyrost w tym momencie jest nieskończenie małą wartością.

Punkty spożywcze i ich klasyfikacja.

Rozważaj pewną funkcję F (x), ciągłe w sąsiedztwie punktu X 0, z wyjątkiem sytuacji, gdy sama może być sama kwestia. Od określenia punktu punktu przerwania wynika z tego, że X \u003d X 0 to punkt przerwy, jeśli funkcja nie jest określona w tym momencie, lub nie jest w nim ciągły.

Należy również zauważyć, że ciągłość funkcji może być jednostronna. Wyjaśnijmy to w następujący sposób.

Funkcja nazywana jest ciągłym prawym.

Jeśli jednostronny limit (patrz wyżej)
Funkcja nazywa się ciągłą po lewej stronie.

Definicja. Punkt x 0 o nazwie punkt rozpylaczafunkcje F (x), jeśli f (x) nie jest zdefiniowane w punkcie x 0 lub nie jest w tym momencie ciągły.

Definicja. Punkt x 0 o nazwie punktowa szczelina 1.Jeśli w tym momencie funkcja f (x) ma skończoną, ale nie równa się nawzajem pozostałych i odpowiednimi limitami.

Aby wykonać warunki tej definicji, nie jest wymagana, że \u200b\u200bfunkcja zostanie określona w punkcie x \u003d x 0, wystarczy, że jest zdefiniowany po lewej i prawej stronie.

Z definicji możemy stwierdzić, że w punkcie punktu przerwania pierwszego rodzaju funkcja może mieć tylko ostateczny skok. W niektórych szczególnych przypadkach, czas łamania pierwszego rodzaju jest czasami nazywany jednorazowypunkt luki, ale porozmawiamy o tym poniżej.

Definicja. Punkt x 0 o nazwie szary punkt drugiego rodzajuJeśli w tym momencie funkcja f (x) nie oznacza co najmniej jednej z jednostronnych limitów lub przynajmniej jednego z nich jest nieskończona.

Ciągłość funkcji w odstępie i segmencie.

Definicja. Funkcja F (X) jest nazywana ciągły w przedziale (segment)Jeśli jest ciągły w dowolnym miejscu w przedziale (segment).

Nie wymaga ciągłości funkcji na końcach segmentu lub interwału, konieczne jest tylko jednostronna ciągłość na końcach segmentu lub interwału.

Właściwości funkcji ciągły w segmencie.

Nieruchomość 1: (Pierwszy twierdzenie Weierstrass (Weierstrass Karl (1815-1897) jest niemieckim matematykiem)). Funkcja ciągła w segmencie jest ograniczona w tym segmencie, tj. Segment jest zadowolony ze stanu -M  F (x)  M.

Dowodem tej właściwości opiera się na fakcie, że funkcja jest ciągła w punkcie X 0 jest ograniczona w niektórych z jego dzielnicach, a jeśli podzielisz segment do nieskończonej liczby segmentów, które są "dokręcone" do punktu x 0, Wtedy powstaje niektóre sąsiedztwo punktu X 0.

Nieruchomość 2: Funkcja ciągła w segmencie przejmuje go największe i najmniejsze wartości.

Te. Istnieją takie wartości x 1 i x 2, że f (x 1) \u003d m, f (x 2) \u003d m, i

m  f (x)  m

Należy pamiętać, że te największe i najmniejsze wartości funkcji mogą przyjąć segment i kilka razy (na przykład - F (x) \u003d Sinx).

Nazywa się różnicę między największą a najmniejszą wartością funkcji w segmencie oscylacjafunkcje w segmencie.

Nieruchomość 3: (Drugi twierdzenie Bolzano - Cauchy). Funkcja ciągła w segmencie nabiera tego segmentu wszystkie wartości między dwiema dowolnymi wartościami.

Nieruchomość 4: Jeśli funkcja F (x) jest ciągła w punkcie x \u003d x 0, istnieje pewne sąsiedztwo punktu x 0, w którym funkcja zapisuje znak.

Nieruchomość 5: (Pierwszy twierdzenie Bolzano (1781-1848) - Cauchy). Jeśli funkcja F (X) jest ciągła w segmencie i ma na końcach segmentu Wartości przeciwnych znaków, istnieje taki punkt w tym segmencie, gdzie f (x) \u003d 0.

Te. Jeśli znak (f (a))  znak (f (b)), a następnie  x 0: f (x 0) \u003d 0.

Przykład.

w punkcie X \u003d -1, funkcja jest ciągła w punkcie X \u003d 1 punkt łamania pierwszego rodzaju

w.

Przykład. Przeglądaj ciągłość funkcji i określić typ punktów szczelin, jeśli są.

w punkcie X \u003d 0, funkcja jest ciągła w punkcie X \u003d 1 punkt punktu przerwania pierwszego rodzaju