Równanie charakterystyczne. Pierwiastki równania charakterystycznego. Stałe czasowe. Czas przejścia. Metody zestawiania równania charakterystycznego Dlaczego potrzebujesz równania charakterystycznego

Równanie charakterystyczne jest obliczane dla obwodu po przełączeniu. Można go uzyskać w następujący sposób:

• bezpośrednio w oparciu o równanie różniczkowe postaci (2) (patrz wykład nr 24), tj. poprzez wyłączenie z układu równań opisującego stan elektromagnetyczny obwodu w oparciu o pierwszą i drugą zasadę Kirchhoffa wszystkie nieznane wielkości z wyjątkiem jednej, w odniesieniu do której zapisane jest równanie (2);
• za pomocą wyrażenia na impedancję wejściową sinusoidalnego obwodu prądowego;
• na podstawie wyrażenia głównego wyznacznika.

Według pierwszej metody, na poprzednim wykładzie otrzymano równanie różniczkowe dotyczące napięcia na kondensatorze dla szeregowego obwodu R-L-C, na podstawie którego zapisano równanie charakterystyczne.

Należy zauważyć, że ponieważ obwód liniowy objęty jest jednym procesem przejściowym, pierwiastki równania charakterystycznego są wspólne dla wszystkich wolnych składowych napięć i prądów gałęzi obwodu, których parametry zawarte są w równaniu charakterystycznym. Zatem zgodnie z pierwszym sposobem układania równania charakterystycznego jako zmienną, względem której jest zapisana, można wybrać dowolną zmienną.

Rozważmy zastosowanie drugiej i trzeciej metody układania równania charakterystycznego na przykładzie obwodu z ryc. 1.

Skład równania charakterystycznego metodą rezystancji wejściowej jest następujący:

jest nagrany impedancja wejściowa obwody prądu przemiennego;

jw zastępuje się operatorem p;

wynikowe wyrażenie jest równe zero.

Równanie

pokrywa się z charakterystyczną.

Należy podkreślić, że rezystancję wejściową można zapisać w odniesieniu do punktu przerwania dowolnej gałęzi obwodu. W tym przypadku aktywną sieć dwuterminalową zastępuje się siecią pasywną, analogicznie do metody generatora zastępczego. Ta metoda komponowania równania charakterystycznego zakłada brak w obwodzie gałęzi sprzężonych magnetycznie; jeśli takie istnieją, należy przeprowadzić ich wstępne odwiązanie.

Dla obwodu z rys. 1 w odniesieniu do zacisków źródłowych

.

Zastępując jw przez p i przyrównując wynikowe wyrażenie do zera, piszemy

.

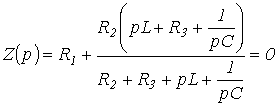
(1)

Podczas kompilowania równania charakterystycznego na podstawie wyrażenia głównego wyznacznika, liczby równania algebraiczne, na podstawie którego napisano, jest równa liczbie nieznanych składowych prądu swobodnego. Algebraizacja pierwotnego układu całkowania równania różniczkowe, skompilowany na przykład na podstawie praw Kirchhoffa lub metodą prądu pętlowego, odbywa się poprzez zastąpienie symboli odpowiednio różniczkowania i całkowania mnożeniem i dzieleniem przez operatora p. Równanie charakterystyczne otrzymuje się przez zrównanie zapisanego wyznacznika z zerem. Ponieważ wyrażenie na wyznacznik główny nie zależy od prawych stron układu równań niejednorodnych, można je zestawić na podstawie układu równań zapisanych dla prądów całkowitych.

Dla obwodu z rys. 1 algebraiczny układ równań oparty na metodzie prądu pętlowego ma postać

Stąd wyrażenie na główny wyznacznik tego układu

Przyrównując D do zera, otrzymujemy wynik podobny do (1).

Ogólna metodologia obliczania procesów przejściowych metodą klasyczną

Ogólnie metodologia obliczania procesów przejściowych metodą klasyczną obejmuje następujące kroki:

Przykłady obliczania procesów przejściowych metodą klasyczną

1. Procesy przejściowe w Łańcuchy R-L po podłączeniu do źródła napięcia

Takie procesy zachodzą np. podczas podłączania elektromagnesów, transformatorów, silników elektrycznych itp. do źródła zasilania.

Rozważmy dwa przypadki:

Zgodnie z rozważaną metodą prądu w obwodzie na ryc. 2 można napisać

Równanie charakterystyczne

stąd stała czasowa .

Zatem,

.

(5)

Podstawiając (4) i (5) do relacji (3) piszemy

.

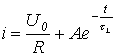Zgodnie z pierwszym prawem komutacji. Następnie

,

Zatem prąd w obwodzie podczas procesu przejściowego opisuje równanie

,

a napięcie na cewce jest podane przez

.

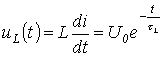Jakościowy wygląd krzywych i odpowiadający otrzymanym rozwiązaniom przedstawiono na ryc. 3.

Dla drugiego typu źródła składową wymuszoną oblicza się metodą symboliczną:

,

Wyrażenie wolnej składowej nie zależy od rodzaju źródła napięcia. Stąd,

.

Od tego czasu

Zatem w końcu dostajemy

.

(6)

Analiza otrzymanego wyrażenia (6) pokazuje:

Jeśli jest to znaczna wielkość, to przez pół okresu wolny składnik nie zmniejsza się znacząco. W takim przypadku maksymalna wartość prądu przejściowego może znacznie przekroczyć amplitudę prądu stanu ustalonego. Jak widać z rys. 4, gdzie

, maksymalny prąd występuje po ok. . W limicie o godz.

Zatem dla obwodu liniowego maksymalna wartość prądu przejściowego nie może przekroczyć dwukrotności amplitudy prądu wymuszonego: .

Podobnie dla obwodu liniowego z kondensatorem: jeśli w chwili załączenia wymuszone napięcie jest równe jego wartości amplitudy, a stała czasowa obwodu jest wystarczająco duża, to po około połowie okresu napięcie na kondensatorze osiąga wartość maksymalną , która nie może przekroczyć dwukrotności amplitudy napięcia wymuszonego: .

2. Procesy przejściowe podczas odłączania cewki indukcyjnej od źródła zasilania

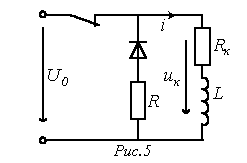
Po otwarciu kluczyka w obwodzie pokazanym na ryc. 5 wymuszona składowa prądu przez cewkę indukcyjną.

Równanie charakterystyczne

,

Gdzie I .

Zgodnie z pierwszym prawem komutacji

.

Zatem wyrażenie na prąd przejściowy to

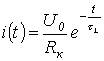
i napięcie na cewce

.

(7)

Analiza (7) pokazuje, że w przypadku otwarcia obwodów zawierających elementy indukcyjne mogą wystąpić duże przepięcia, które bez podjęcia specjalnych działań mogą spowodować uszkodzenie sprzętu. Rzeczywiście, kiedy Moduł napięciowy na cewce w momencie załączenia będzie wielokrotnie wyższy od napięcia źródła: . W przypadku braku rezystora gaszącego R, do styków otwierających klucza przykładane jest określone napięcie, w wyniku czego między nimi powstaje łuk.

3. Ładowanie i rozładowywanie kondensatora

Po przesunięciu kluczyka do pozycji 1 (patrz rys. 6) rozpoczyna się proces ładowania kondensatora:

.

Wymuszona składowa napięcia na kondensatorze.

Z równania charakterystycznego

korzeń jest określony . Stąd stała czasowa.

Tryb swobodny obwodu nie jest zależny od źródeł energii, determinuje go jedynie konstrukcja obwodu i parametry jego elementów. Wynika z tego, że pierwiastki równania charakterystycznego p1, p2,…, pn będą dla wszystkich takie same funkcje zmienne(prądy i napięcia).

Równanie charakterystyczne można zbudować różnymi metodami. Pierwsza metoda jest klasyczna, gdy równanie charakterystyczne jest kompilowane ściśle według równania różniczkowego według schematu klasycznego. Przy obliczaniu procesów przejściowych w złożony schemat układ równań różniczkowych „m” jest kompilowany zgodnie z prawami Kirchhoffa dla schematu obwodu po przełączeniu. Ponieważ pierwiastki równania charakterystycznego są wspólne dla wszystkich zmiennych, rozwiązanie układu równań różniczkowych przeprowadza się w odniesieniu do dowolnej zmiennej (opcjonalnie). W wyniku rozwiązania otrzymuje się niejednorodne równanie różniczkowe z jedną zmienną. Ułóż równanie charakterystyczne zgodnie z otrzymanym równaniem różniczkowym i określ jego pierwiastki.

Przykład. Narysuj równanie charakterystyczne i określ jego pierwiastki dla zmiennych przedstawionych na wykresie na ryc. 59.1. Parametry elementów podano w formie ogólnej.

Układ równań różniczkowych według praw Kirchhoffa:

Rozwiążmy układ równań dla zmiennej i3, w wyniku czego otrzymamy niejednorodne równanie różniczkowe:

Drugi sposób zestawienia równania charakterystycznego polega na przyrównaniu do zera głównego wyznacznika układu równań Kirchhoffa dla zmiennych składowych swobodnych.

Niech wolna składowa dowolnego prądu ma postać iksv = Аkept, wówczas:

Układ równań na składowe swobodne otrzymuje się z układu równań różniczkowych Kirchhoffa zastępując pochodne zmiennych przez współczynnik p, a całki przez 1/p. Dla rozważanego przykładu układ równań dla składników swobodnych ma postać:

Równanie charakterystyczne i jego pierwiastek:

Trzeci sposób zestawienia równania charakterystycznego (inżynierskiego) polega na zrównaniu rezystancji operatora wejściowego obwodu z zerem w stosunku do dowolnej jego gałęzi.

Opór operatora elementu uzyskuje się z jego złożonego oporu, po prostu zastępując współczynnik jω p

Dla omawianego przykładu:

Trzecia metoda jest najprostsza i najbardziej ekonomiczna, dlatego najczęściej stosowana jest przy obliczaniu procesów przejściowych w obwodach elektrycznych.

Pierwiastki równania charakterystycznego charakteryzują proces przejściowy swobodny w obwodzie bez źródeł energii. Proces ten zachodzi ze stratami energii i dlatego z czasem zanika.

W ogólnym przypadku rząd równania różniczkowego opisującego proces przejściowy w obwodzie, a w konsekwencji stopień równania charakterystycznego i liczba jego pierwiastków są równe liczbie niezależnych warunki początkowe lub liczbę niezależnych urządzeń magazynujących energię (cewki L i kondensatory C).

Jeżeli schemat obwodu zawiera równolegle połączone kondensatory C1, C2,... lub szeregowo połączone cewki L1, L2,..., to przy obliczaniu procesów przejściowych należy je zastąpić jednym równoważnym elementem SE = C1 + C2+... lub LE = L1 + L2+... Zatem, widok ogólny

rozwiązania dla dowolnej zmiennej przy obliczaniu procesu przejściowego można zestawić jedynie na podstawie analizy schematu obwodu, bez kompilowania i rozwiązywania układu równań różniczkowych.

) Dla przykładu omówionego powyżej. = ||A||ik N

1 odejmując wartość λ od elementów przekątnych. Wyznacznikiem tym jest wielomian względem X – wielomian charakterystyczny. Po otwarciu X. u. jest napisane tak: Gdzie = S 1 + 11 +... 22 anna - tzw ślad matrycy, S2 ik- suma wszystkich nieletnich większych drugiego rzędu, tj. małoletnich postaci i k), itd., oraz S Dla przykładu omówionego powyżej.- wyznacznik macierzy ik. Korzenie H. u. λ 1 , λ 2 ,..., λ Dla przykładu omówionego powyżej. nazywane są wartościami własnymi macierzy . Dla prawdziwej macierzy symetrycznej, a także dla macierzy hermitowskiej, wszystkie λ k . Dla prawdziwej macierzy symetrycznej, a także dla macierzy hermitowskiej, wszystkie λ są rzeczywiste, prawdziwa macierz skośno-symetryczna ma wszystkie λ . Dla prawdziwej macierzy symetrycznej, a także dla macierzy hermitowskiej, wszystkie λ| = 1.

liczby czysto urojone; w przypadku rzeczywistej macierzy ortogonalnej, jak i macierzy unitarnej, wszystkie |λ

H.u. Można je znaleźć w wielu różnych dziedzinach matematyki, mechaniki, fizyki i technologii. W astronomii, określając świeckie perturbacje planet, dochodzą także do równań chemicznych; stąd drugie imię X. u. - odwieczne równanie.

2) H. u. liniowe równanie różniczkowe o stałych współczynnikachλ 0 (y) + N (1 rok) +... + n-1 + n-1 y” = 0

każdy Równanie algebraiczne, które otrzymuje się z zadanego równania różniczkowego po zmianie funkcji Na

2) H. u. liniowe równanie różniczkowe o stałych współczynnikachλ ik + i jego pochodne przez odpowiednie potęgi λ, czyli równanieλ 1 + ... + n-1 n-1 + n-1 y” = 0.

y” Równanie algebraiczne, które otrzymuje się z zadanego równania różniczkowego po zmianie funkcji = Równanie to uzyskuje się poprzez znalezienie konkretnego rozwiązania postaci λ se X

dla danego równania różniczkowego. Dla układu liniowych równań różniczkowych

H.u. zapisane za pomocą wyznacznika H.u. matryce =

A Duży Encyklopedia radziecka. 1969-1978 .

. - M .: Encyklopedia radziecka

Zobacz, czym jest „Równanie charakterystyczne” w innych słownikach: W wielu przypadkach, występujące w układach, opisuje się układem zwykłych liniowych równań różniczkowych o stałych współczynnikach, które w dość ogólnym przypadku można sprowadzić do równania różniczkowego ... Encyklopedia technologii

Równanie algebraiczne postaci: Wyznacznik w tym wzorze otrzymuje się z wyznacznika macierzy odejmując wartość x od elementów przekątnych; reprezentuje wielomian w x i nazywany jest wielomianem charakterystycznym... Wielki słownik encyklopedyczny

równanie charakterystyczne- - [V.A. Semenow. Angielsko-rosyjski słownik zabezpieczeń przekaźników] Tematy zabezpieczeń przekaźników EN równanie charakterystyczne ... Przewodnik tłumacza technicznego

Równanie algebraiczne postaci. Wyznacznik w tym wzorze otrzymuje się z wyznacznika macierzy x elementów przekątnych; jest to wielomian w x i nazywany jest wielomianem charakterystycznym. * * * CHARAKTERYSTYKA… … Słownik encyklopedyczny

równanie charakterystyczne- būdingoji lygtis statusas T sritis automatika atitikmenys: engl. równanie charakterystyczne; równanie wydajności vok. charakteristische Gleichung, f; Stammgleichung, f rus. równanie charakterystyczne, n pranc. équation caractéristique, f … Automatikos terminų žodynas

równanie charakterystyczne- būdingoji lygtis statusas T sritis fizika atitikmenys: engl. równanie charakterystyczne; równanie wydajności vok. Charakteristische Gleichung, f rus. równanie charakterystyczne, n pranc. équation caractéristique, f … Fizikos terminų žodynas

równanie charakterystyczne Encyklopedia „Lotnictwo”

równanie charakterystyczne- równanie charakterystyczne. W wielu przypadkach procesy fizyczne zachodzące w układach opisuje się układem zwyczajnych liniowych równań różniczkowych o stałych współczynnikach, które w dość ogólnym przypadku można zredukować... Encyklopedia „Lotnictwo”

Równanie świeckie, patrz art. Charakterystyczny wielomian... Encyklopedia matematyczna

Wielomian charakterystyczny to wielomian określający wartości własne macierzy. Inne znaczenie: charakterystyczny wielomian powtarzalności liniowej jest wielomianem. Spis treści 1 Definicja… Wikipedia

Książki

• Charakterystyczne pierścienie Liego i nieliniowe równania całkowalne, Zhiber A.V.. Książka poświęcona jest systematycznej prezentacji algebraicznego podejścia do badania nieliniowych całkowalnych równań różniczkowych cząstkowych i ich dyskretnych analogów, w oparciu o koncepcję...

Równanie charakterystyczne ma postać:

Aby określić rodzaj składowej swobodnej, należy ułożyć i rozwiązać równanie charakterystyczne: z(p) = 0. Aby zapisać równanie charakterystyczne, należy narysować schemat, na którym należy zastąpić wszystkie źródła pola elektromagnetycznego i prądu przez ich własne wnętrze opór i opór przyjąć indukcyjność i pojemność odpowiednio równe Pl i , wówczas należy przerwać dowolną gałąź tego obwodu, zapisać jej początkową rezystancję względem punktów przerwania, przyrównać ją do zera, rozwiązać i wyznaczyć pierwiastki p, jeśli pierwiastki okaże się naprawdę ujemny, wówczas wolny składnik żądanej funkcji:

,gdzie m jest liczbą pierwiastków równania;

Korzenie; - na stałe zintegrowany.

Jeżeli pierwiastki równania znaku okażą się sprzężeniem złożonym, wówczas stan wolny będzie miał postać:

gdzie jest częstotliwość drgań swobodnych;

Początkowa faza swobodnych oscylacji.

8.Czas przejścia. Wyznaczenie praktycznie t pp. Obliczanie czasu procesu przejścia.

Czas procesu przejściowego zależy od współczynnika tłumienia. Wartość odwrotna nazywana jest stałą czasową i jest czas, w trakcie przy czym wartość składowej swobodnej procesu nieustalonego zmniejszy się e=2,72 razy. Wartość zależy od obwodu i parametrów. Zatem dla obwodu z połączenie szeregowe r i L = oraz w połączeniu szeregowym

Zakończenie procesu przejścia w 95% 3.

Najłatwiej skonstruować krzywe składowych swobodnych procesu nieustalonego, ustawiając wartości czasu t na 0, ,2..... Jeżeli istnieje kilka pierwiastków rzeczywistych, to wynikową krzywą otrzymuje się przez zsumowanie rzędne poszczególnych terminów (ryc. 1.)

Rysunek 1:

9.10, Proces przejściowy w r, C – obwody po podłączeniu do źródła Napięcie stałe. Wykonaj analizę metodą klasyczną; podać wyrażenia analityczne dla UC (t); iC(t); grafika. (Metoda klasyczna).

Równanie stanu obwodu rC po przełączeniu wygląda następująco:

(1) lub rC (2)

Jego rozwiązanie:

Pojemność C po zamknięciu klucza w momencie t będzie ładowana do stałej wartości

Ponieważ warunki początkowe wynoszą zero, zgodnie z prawem komutacji w t=0, lub 0=A, skąd A=-E.

Rozwiązanie równania (2) będzie miało postać:

Prąd obwodu i(t)=C

Rysunek 1.

Rysunek 2.

Wykresy zmian napięcia i prądu i(t) pokazano na rysunkach 1 i 2. Z rysunków widać, że napięcie na kondensatorze rośnie wykładniczo od 0 do E, natomiast natężenie prądu w momencie załączenia gwałtownie osiąga wartość E/r, a następnie maleje do zera.

11.12.Proces przejściowy w r, C – obwody po podłączeniu do źródła napięcia sinusoidalnego. Wykonaj analizę metodą klasyczną; podać wyrażenia analityczne dla UC (t); iC(t); grafika. (Metoda klasyczna).

Równanie stanu obwodu rC w trybie przejściowym jest następujące

rC .

Rozwiązanie tego równania:

Darmowy komponent

gdzie =rC

Ponieważ obwód jest liniowy, to z efektem sinusoidalnym i w stanie ustalonym, napięcie na kondensatorze również będzie się zmieniać zgodnie z prawem sinusoidalnym wraz z częstotliwością efektu wejściowego. Dlatego do określenia = użyjemy metody złożonych amplitud :

;

Biorąc pod uwagę, że j= , otrzymujemy:

Stała całkowania A składnika wolnego

Znajdźmy z warunków początkowych w obwodzie, biorąc pod uwagę prawo komutacji:

.W t=0 ostatnie wyrażenie ma postać

Gdzie A=-

Dodając składniki i , otrzymujemy ostateczne wyrażenie napięcia na kondensatorze w trybie przejściowym:

= + = - (1)

Analiza wyrażenia (1) pokazuje, że proces przejściowy w obwodzie rC pod wpływem sinusoidalnym zależy od fazy początkowej emf źródła w momencie przełączenia oraz od stałej czasowej obwodu rC.

Jeżeli , to natychmiast po przełączeniu w obwodzie wystąpi =0 i stan ustalony, tj.

Gdy napięcie = - , tj. Napięcie na kondensatorze natychmiast po przełączeniu może osiągnąć prawie dwukrotność znaku dodatniego, a następnie stopniowo zbliżać się do =.

Różnica faz doprowadzi równanie (1) do postaci:

Różnica między tym trybem a poprzednim polega na tym, że napięcie na kondensatorze natychmiast po przełączeniu może osiągnąć prawie dwukrotnie wartość ujemną.

Dla rozpatrywanego obwodu Rc z sinusoidalnym źródłem prądu w stanie ustalonym, faza początkowa napięcie wejściowe nie odgrywa żadnej roli, ale w procesie transformacji jego wpływ jest znaczący.

13.Proces przejściowy w obwodach r, L, C – przy podłączeniu do źródła napięcia stałego. Proces wsadowy. Wyrażenia analityczne dla i(t), grafika. (Metoda klasyczna).

Korzenie są prawdziwe, negatywne, inne.

I(t)=Ja usta +A1e p 1 t +A2e p 2 t

Proces jest okresowy:

t=0 (i(0)=A1+A2; A1=-A2

{

t=0 i l (0)*r+L +Uc(0)=E A1=-A2= ()

ja l (t) = ( )

14.Proces przejściowy w r, L, C – obwody przy podłączeniu do źródła napięcia stałego. Proces krytyczny. Wyrażenia analityczne dla i(t), grafika. (Metoda klasyczna).

i l (t)=ja usta +(B1+B2*t)*

t=0: i l (0)=β1=0

Jeśli pierwiastki okażą się prawdziwe, ujemne, równe, wówczas proces jest krytyczny.

15.Proces przejściowy w r, L, C – obwody przy podłączeniu do źródła napięcia stałego. Proces oscylacyjny. Wyrażenie analityczne dla i(t), grafika. (Metoda klasyczna).

P t = -δ±j*ω St ω St =

Korzenie są rzeczywiste ujemne, jakiś złożony koniugat.

i l (t)=i usta A1e - δt *sin(ω St t+ψ)

i l (t)=i usta +(M*cos ω światło t+N*sin ω światło t)*

ja l (t) = * = *

16. Proces przejściowy w r, L, C – obwody po podłączeniu do źródła napięcia sinusoidalnego. Proces aperiodyczny. Wyrażenie analityczne dla i(t), grafika. (Metoda klasyczna).

R(t)=E max *sin(ωt+ψ)

2.

W klasycznym przypadku liczba równań jest równa liczbie gałęzi obwodu

Metoda znajduje rozwiązanie w postaci sumy rozwiązania ogólnego i szczegółowego. Obliczenie procesu przejściowego opisuje układ równań różniczkowych zwyczajnych skompilowany jedną z metod obliczeniowych dla chwilowych wartości funkcji czasu. Rozwiązanie dla każdej zmiennej tego układu można znaleźć w postaci sumy rozwiązań ogólnych i szczegółowych. Do ułożenia równania można zastosować: metodę opartą na zastosowaniu praw Kirchhoffa, metodę potencjałów węzłowych, metodę prądów pętlicowych itp. Przykładowo układ równań różniczkowych utworzony po komutacji zgodnie z pierwszym i drugim prawem Kirchhoffa ma postać:

Na przykład,

Liczba równań w tym przypadku jest równa liczbie gałęzi obwodu. Niech trzeba będzie znaleźć prąd i k w gałęzi o numerze K. Eliminując kolejno prądy gałęzi, w rezultacie otrzymamy prąd i k i jego pochodne aż do rzędu n:

Rząd równania różniczkowego n jest określony przez liczbę niezależnych elementów reaktywnych obwodu (m). Zwykle n=m, ale w zależności od metody połączenia może być tak, że n

Elementy pojemnościowe połączone szeregowo można zastąpić jednym elementem, tak jak elementy indukcyjne połączone równolegle można zastąpić jednym równoważnym. Rysunek 9.5 przedstawia wymianę 2 kondensatorów połączonych szeregowo na jeden równoważny.

Ogólnie rząd równania różniczkowego n jest równy: n=n lc -n ce -n lj, gdzie n lc to liczba elementów biernych (L i C) w obwodzie, n ce to liczba elementów pojemnościowych obwody, n lj to liczba węzłów lub sekcji indukcyjnych.

Przez pojemność rozumie się obwód składający się z elementów pojemnościowych lub elementów pojemnościowych i idealnych źródeł pola elektromagnetycznego, rys. 9.6.a. Przez indukcyjność rozumie się węzeł, w którym zbiegają się gałęzie indukcyjne lub gałęzie indukcyjne i źródła prądu (rys. 9.6.b), lub odcinki, które przecinają wyłącznie gałęzie indukcyjne lub gałęzie indukcyjne i źródła prądu.

Należy pamiętać, że etap sporządzania równania różniczkowego nie jest obowiązkowy, a prąd lub napięcie przejścia można znaleźć bez sporządzania równania. Jak wskazano, w klasycznej metodzie obliczania procesów przejściowych rozwiązujących równania jest reprezentowany jako suma rozwiązań ogólnych i szczegółowych.

Szczególne rozwiązanie opisuje reżim zwany przymusowym. Rozwiązanie jednorodnego równania (prawa strona wynosi zero) opisuje proces przy braku zewnętrznych źródeł pola elektromagnetycznego i prądu i nazywa się swobodnym. Odpowiednio uwzględniane są swobodne i wymuszone prądy, napięcia i ładunki.

Zatem prąd w gałęzi o numerze K jest reprezentowany jako suma.

Definicja. Równanie charakterystyczne operatora liniowego f jest równaniem postaci , gdzie λ jest dowolną liczbą rzeczywistą, A jest macierzą operatora liniowego, E jest macierzą jednostkową tego samego rzędu.

Wielomian zwany charakterystyczny wielomian macierz A (operator liniowy f). W postaci macierzowej równanie charakterystyczne ma następującą postać:

Lub

.

W konsekwencji przyrównując charakterystyczny wielomian do zera, otrzymujemy równanie stopnia y, gdzie λ jest niewiadomą, otrzymujemy wartości jej pierwiastków – liczby charakterystyczne tej macierzy. Charakterystyczne pierwiastki odgrywają ważną rolę w wielu obszarach matematyki. Rozważmy jedno z zastosowań pierwiastków charakterystycznych - bardzo ważnego narzędzia w badaniu przestrzeni liniowych, a także w rozwiązywaniu wielu stosowanych problemów algebry liniowej.

Zbiór wszystkich pierwiastków równania charakterystycznego nazywa się widmem operatora F(każdy pierwiastek jest rozpatrywany z krotnością, jaką ma w równaniu charakterystycznym).

Przykład. Znajdź charakterystyczne pierwiastki macierzy.

Stwórzmy macierz

Przyrównując charakterystyczny wielomian do zera, otrzymujemy równanie kwadratowe

Wtedy pierwiastki równania są równe .

Definicja. Niech f będzie operatorem liniowym przestrzeni i niech będzie jakimś niezerowym wektorem, dla którego zachodzi równość

gdzie jest liczbą rzeczywistą. Następnie wektor nazywany jest wektorem własnym operatora i macierzą jego operatora, wartością własną lub wartością własną transformacji. W tym przypadku mówi się, że wektor własny odnosi się do wartości własnej.

Wektory własne odgrywają ważną rolę zarówno w samej matematyce, jak i w jej zastosowaniach. Na przykład rezonans, w którym częstotliwości drgań własnych układu pokrywają się z częstotliwością drgań sił zewnętrznych. W matematyce wektory własne są przydatne w rozwiązywaniu układów równań różniczkowych.

Twierdzenie. Jeżeli operator liniowy f ma w swojej bazie macierz A (pierwsza baza) i macierz B w swojej bazie (druga baza), to zachodzi równość: .

W konsekwencji przy przejściu do nowej podstawy wielomian charakterystyczny operatora liniowego nie ulega zmianie.

◌ Jeżeli T jest macierzą przejścia z pierwszej bazy do drugiej, to . Następnie przekształcamy prawą stronę równości ●

Twierdzenie. Aby liczba λ 0 z ciała P była wartością własną wektora przestrzeni L n nad P, konieczne i wystarczające jest, aby liczba λ 0 była pierwiastkiem charakterystycznym operatora f.

Doktor. I. Konieczność. Pozwalać λ 0 wartość własna operatora F, potem w Ln istnieje wektor własny taki, że .

Pozwalać jest zatem w jakiejś podstawie jego linią współrzędnych

Z drugiej strony, ponieważ , gdzie jest zatem macierzą operatora liniowego w danej bazie

Porównując prawe strony (1) i (2) otrzymujemy:

(3)

Równość (3) oznacza wektor liczbowy ze współrzędnymi jest rozwiązaniem następującego układu równań (4).

(4)

Wektor jest różny od zera (ponieważ jest własny), zatem układ (4) ma rozwiązanie niezerowe, zatem jego wyznacznikiem jest 0.

(5)

a zatem wyznacznik transpozycyjny jest równy 0.

(6)

Jeżeli schemat obwodu zawiera równolegle połączone kondensatory C1, C2,... lub szeregowo połączone cewki L1, L2,..., to przy obliczaniu procesów przejściowych należy je zastąpić jednym równoważnym elementem SE = C1 + C2+... lub LE = L1 + L2+... λ 0 – pierwiastek równania charakterystycznego.

II. Adekwatność. Pozwalać λ 0 – charakterystyczny pierwiastek operatora w jakiejś podstawie . Udowodnijmy to λ 0 jest wartością własną operatora A.

Rzeczywiście, jeśli λ 0 jest pierwiastkiem charakterystycznym, wówczas spełniona zostanie równość (6), a co za tym idzie równość (5), a to będzie oznaczać, że układ (4) ma rozwiązania niezerowe.

Wybierzmy jakieś niezerowe rozwiązanie układu (4): wektor numeryczny . Wtedy równości (3) są spełnione.

Rozważmy wektor i dla niego zostanie spełniona równość (2) i na mocy wzoru obowiązuje równość (1), gdzie jest macierz operatora w bazie W. Implikuje to równość, co oznacza, że ​​wektor jest wektorem własnym operatora, któremu odpowiada wartość własna λ 0 . To właśnie należało udowodnić. Twierdzenie zostało udowodnione.

Komentarz. Aby znaleźć wartości własne operatora, należy ułożyć i rozwiązać równanie (5). Aby znaleźć wektory własne operatora, należy utworzyć układ równań (4) i znaleźć podstawowy zbiór rozwiązań tego układu.

Aby kontrolować poprawność obliczeń wartości własnych (mogą być zbieżne lub złożone), stosuje się dwa fakty:

1) , gdzie ostatnia suma macierzy śladowej jest sumą elementów przekątnych.

2) .

Przykład. Znajdź wartości własne i wektory własne .

Przyrównując do zera otrzymujemy . .

3) . , .

Niech będzie zmienną wolną, wtedy otrzymamy wektor .

Ćwiczenia. Sprawdź wektor.

.