Fungsi besar tak terhingga mempunyai sifatnya. Takrif fungsi yang tidak terhingga besar. Fungsi tak terhingga

Rumah

Fasad kaca

Takrif jujukan yang tidak terhingga besar diberikan. Konsep kejiranan titik pada infiniti dipertimbangkan. Takrif sejagat bagi had jujukan diberikan, yang digunakan untuk kedua-dua had terhingga dan tak terhingga. Contoh penggunaan takrifan jujukan yang tidak terhingga besar dipertimbangkan.

kandungan

Lihat juga: Menentukan Had Urutan

Definisi

Susulan (βn) dipanggil urutan besar tak terhingga, jika untuk sebarang nombor M, walau bagaimanapun besar, wujud sedemikian nombor asli N M bergantung kepada M supaya untuk semua n > N M semula jadi, ketidaksamaan berikut berlaku:
|βn | >M.
Dalam kes ini mereka menulis
.
Atau di .
Mereka mengatakan bahawa ia cenderung kepada infiniti, atau menumpu kepada infiniti.

Jika, bermula dari beberapa nombor N 0 , Itu
( menumpu kepada tambah infiniti).
Jika kemudian
( menumpu kepada tolak infiniti).

Marilah kita menulis definisi ini menggunakan simbol logik kewujudan dan kesejagatan:
(1) .
(2) .
(3) .

Jujukan dengan had (2) dan (3) ialah kes khas bagi jujukan yang tidak terhingga besar (1). Daripada takrifan ini, ia mengikuti bahawa jika had jujukan adalah sama dengan tambah atau tolak infiniti, maka ia juga sama dengan infiniti:
.
Sebaliknya, tentu saja, tidak benar. Ahli jujukan mungkin mempunyai tanda berselang-seli. Dalam kes ini, had boleh sama dengan infiniti, tetapi tanpa tanda tertentu.

Ambil perhatian juga bahawa jika sesetengah sifat memegang untuk jujukan arbitrari dengan had yang sama dengan infiniti, maka sifat yang sama memegang untuk jujukan yang hadnya sama dengan tambah atau tolak infiniti.

Dalam banyak buku teks kalkulus, takrifan jujukan yang tidak terhingga besar menyatakan bahawa nombor M adalah positif: M > 0 .

Walau bagaimanapun, keperluan ini tidak diperlukan. Jika ia dibatalkan, maka tiada percanggahan yang timbul. Cuma nilai kecil atau negatif tidak menarik minat kita. Kami berminat dengan kelakuan urutan untuk nilai positif M yang besar secara sewenang-wenangnya. > 0 Oleh itu, jika keperluan timbul, maka M boleh dihadkan dari bawah oleh mana-mana nombor yang telah ditetapkan a, iaitu, kita boleh menganggap bahawa M > a.

Apabila kita menentukan ε - kejiranan titik akhir, maka keperluan ε

adalah penting. Untuk nilai negatif, ketidaksamaan tidak boleh dipenuhi sama sekali.

Kejiranan titik di infiniti
Apabila kami mempertimbangkan had terhingga, kami memperkenalkan konsep kejiranan titik. Ingat bahawa kejiranan titik akhir ialah selang terbuka yang mengandungi titik ini. Kita juga boleh memperkenalkan konsep kejiranan titik di infiniti. Biarkan M ialah nombor arbitrari.
Kejiranan titik "infiniti" Biarkan M ialah nombor arbitrari.
, , dipanggil set. Biarkan M ialah nombor arbitrari.

Kejiranan titik "tambah infiniti"
(4) ,
Di sekitar titik "tolak infiniti" 1 Tegasnya, kejiranan titik "infiniti" adalah set 2 di mana M

dan M

- nombor positif sewenang-wenangnya. Kami akan menggunakan definisi pertama, kerana ia lebih mudah. Walaupun, semua yang dinyatakan di bawah juga benar apabila menggunakan definisi (4)..
Kini kita boleh memberikan takrifan bersatu bagi had jujukan yang digunakan untuk kedua-dua had terhingga dan tak terhingga.

Takrif universal had jujukan

Titik a (terhingga atau pada infiniti) ialah had jujukan jika bagi mana-mana kejiranan titik ini terdapat nombor asli N supaya semua unsur jujukan dengan nombor tergolong dalam kejiranan ini.
Oleh itu, jika had wujud, maka di luar kejiranan titik a hanya terdapat bilangan ahli terhingga bagi jujukan, atau set kosong. Syarat ini perlu dan mencukupi. Bukti harta ini adalah sama seperti untuk had terhingga.
Sifat kejiranan bagi jujukan menumpu

Agar titik a (terhingga atau pada infiniti) menjadi had jujukan, adalah perlu dan memadai bahawa di luar mana-mana kejiranan titik ini terdapat bilangan sebutan terhingga bagi jujukan atau set kosong.
Bukti .
Juga kadangkala konsep ε - kejiranan titik pada infiniti diperkenalkan. Ingat bahawa kejiranan ε bagi titik terhingga a ialah set .. Biarkan ε menyatakan kejiranan titik a.
.
Kemudian untuk titik akhir,
;
;
.
Untuk mata di infiniti:

Menggunakan konsep ε-kejiranan, kita boleh memberikan satu lagi definisi universal tentang had jujukan: Titik a (terminal atau pada infiniti) ialah had jujukan jika ada ε > 0 nombor positif
.

terdapat nombor asli N ε bergantung pada ε supaya untuk semua nombor n > N ε sebutan x n tergolong dalam kejiranan ε titik a:
.

Menggunakan simbol logik kewujudan dan kesejagatan, definisi ini boleh ditulis seperti berikut:

Contoh jujukan yang tidak terhingga besar

.
Contoh 1
(1) .
Mari kita tuliskan takrif bagi jujukan yang tidak terhingga besar:
.

Dalam kes kita
.
Kami memperkenalkan nombor dan , menghubungkannya dengan ketaksamaan:
.
Mengikut sifat ketaksamaan, jika dan , maka
Ambil perhatian bahawa ketidaksamaan ini berlaku untuk sebarang n.
Oleh itu, anda boleh memilih seperti ini:

pada ;
.
di .

Jadi, untuk mana-mana satu kita boleh mencari nombor asli yang memenuhi ketaksamaan.

Kemudian untuk semua orang,
.

(2) .
Ini bermakna bahawa .
.

Iaitu, jujukannya tidak terhingga besar.
.
.

Contoh 2
.
Menggunakan takrifan jujukan yang tidak terhingga besar, tunjukkan bahawa

Istilah umum bagi urutan yang diberikan mempunyai bentuk:

Kemudian untuk semua orang,
.

Masukkan nombor dan:
(3) .
Ini bermakna bahawa .
.

Iaitu, jujukannya tidak terhingga besar.
.
Kemudian bagi sesiapa sahaja boleh mencari nombor asli yang memenuhi ketaksamaan, jadi untuk semua ,
.

Ini bermakna bahawa .
.

Contoh 3
.

Mari kita tulis takrifan had jujukan yang sama dengan tolak infiniti:

Kemudian untuk semua orang,
.

Daripada ini jelas bahawa jika dan , maka
.
Oleh kerana bagi mana-mana satu adalah mungkin untuk mencari nombor asli yang memenuhi ketaksamaan, maka
(2) .

Diberi , sebagai N kita boleh mengambil sebarang nombor asli yang memenuhi ketaksamaan berikut: = 1, 2, 3, ... , Itu
;
;
.

Contoh 4
.
Kemudian bagi sesiapa sahaja boleh mencari nombor asli yang memenuhi ketaksamaan, jadi untuk semua ,
.

Mari kita tuliskan istilah umum bagi urutan tersebut:
.
Menggunakan takrifan jujukan yang tidak terhingga besar, tunjukkan bahawa

Mari kita tulis takrifan had jujukan bersamaan dengan tambah infiniti:
Oleh kerana n ialah nombor asli, n
Kami memperkenalkan nombor dan M, menghubungkannya dengan ketaksamaan:

Jadi, untuk sebarang nombor M kita boleh mencari nombor asli yang memenuhi ketaksamaan.

Kemudian untuk semua orang, Sastera terpakai: L.D. Kudryavtsev. Kursus analisis matematik. Jilid 1. Moscow, 2003. CM. Nikolsky. Kursus analisis matematik. Jilid 1. Moscow, 1983. Lihat juga: Fungsi y=f(x) dipanggil sangat kecil di x→a

atau bila

x →∞, jika atau , i.e. tanpa henti=(dipanggil fungsi kecil dipanggil ialah fungsi yang hadnya pada titik tertentu ialah sifar.

Contoh. →∞, jika atau , i.e. tanpa henti 1. Fungsi dipanggil f(x) dipanggil→0.

3. →∞, jika atau , i.e. tanpa henti-1) 2 adalah sangat kecil pada dipanggil→1, sejak (lihat rajah). dipanggil→0.

4. →∞, jika atau , i.e. tanpa henti = 1/dipanggil 2. Fungsi dipanggil→∞.

Marilah kita mewujudkan hubungan penting berikut:

Teorem. Jika fungsi Sastera terpakai: boleh diwakili dengan Fungsi sebagai hasil tambah nombor tetap b dan magnitud tak terhingga α(x): f (x)=b+ α(x) itu.

Sebaliknya, jika , maka f (x)=b+α(x), Di mana a(x) f(x) x→a.

Bukti.

1. Mari kita buktikan bahagian pertama pernyataan itu. Daripada kesamarataan f(x)=b+α(x) sepatutnya |f(x) – b|=| α|. Tetapi sejak a(x) adalah sangat kecil, maka untuk ε sewenang-wenangnya terdapat δ – kejiranan titik a, di hadapan semua orang dipanggil daripada mana, nilai a(x) memuaskan perhubungan |α(x)|< ε. Kemudian |f(x) – b|< ε. Dan ini bermakna bahawa .

2. Jika , maka untuk sebarang ε >0 untuk semua orang X dari beberapa δ – kejiranan suatu titik a kehendak |f(x) – b|< ε. Tetapi jika kita nyatakan f(x) – b= α, Itu |α(x)|< ε, yang bermaksud itu a– sangat kecil.

Mari kita pertimbangkan sifat asas bagi fungsi infinitesimal.

Teorem 1. Jumlah algebra bagi dua, tiga, dan secara amnya sebarang nombor terhingga bagi infinitesimal ialah fungsi infinitesimal.

Bukti. Mari kita berikan bukti untuk dua penggal. biarlah f(x)=α(x)+β(x), di mana dan . Kita perlu membuktikan bahawa untuk ε sewenang-wenangnya sewenang-wenangnya kecil > 0 ditemui δ> 0, supaya untuk dipanggil, memuaskan ketidaksamaan |x – a|<δ , dilaksanakan |f(x)|< ε.

Jadi, mari betulkan nombor arbitrari ε > 0. Oleh kerana mengikut syarat teorem α(x) ialah fungsi yang sangat kecil, maka terdapat δ 1 > 0, iaitu |x – a|< δ 1 kita ada |α(x)|< ε / 2. Begitu juga, sejak β(x) adalah sangat kecil, maka terdapat δ 2 > 0, iaitu |x – a|< δ 2 kita ada | β(x)|< ε / 2.

Mari ambil δ=min(δ 1 , δ2 } .Kemudian di kawasan kejiranan titik a jejari δ setiap ketidaksamaan akan dipenuhi |α(x)|< ε / 2 dan | β(x)|< ε / 2. Oleh itu, dalam kejiranan ini akan ada

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

mereka. |f(x)|< ε, itulah yang perlu dibuktikan.

Teorem 2. Hasil darab fungsi yang sangat kecil a(x) untuk fungsi terhad →∞, jika atau , i.e. tanpa henti Lihat juga: Fungsi(atau bila x→∞) ialah fungsi yang sangat kecil.

Bukti. Sejak fungsi →∞, jika atau , i.e. tanpa henti adalah terhad, maka ada nombor M supaya untuk semua nilai dipanggil dari beberapa kawasan kejiranan a|f(x)|≤M. Lebih-lebih lagi, sejak a(x) ialah fungsi infinitesimal di Fungsi, kemudian untuk ε sewenang-wenangnya > 0 terdapat kejiranan titik a, di mana ketidaksamaan akan berlaku |α(x)|< ε /M. Kemudian di kawasan kejiranan yang lebih kecil ini kita ada | αf|< ε /M= ε. Dan ini bermakna af– sangat kecil. Untuk majlis itu x→∞ pembuktian dijalankan sama.

Daripada teorem terbukti ia berikut:

Akibat 1. Jika dan, maka.

Akibat 2. Jika dan c= const, kemudian .

Teorem 3. Nisbah fungsi infinitesimal α(x) setiap fungsi →∞, jika atau , i.e. tanpa henti, yang hadnya berbeza daripada sifar, ialah fungsi yang sangat kecil.

Bukti. biarlah . Kemudian 1 /f(x) terdapat fungsi terhad. Oleh itu, pecahan ialah hasil darab bagi fungsi tak terhingga dan fungsi terhad, i.e. fungsi adalah sangat kecil.

Kalkulus infinitesimal dan larges

kalkulus infinitesimal- pengiraan yang dilakukan dengan kuantiti tak terhingga, di mana hasil terbitan dianggap sebagai jumlah tak terhingga bagi infinite. Kalkulus infinitesimal ialah konsep umum untuk kalkulus pembezaan dan kamiran, yang membentuk asas matematik moden yang lebih tinggi. Konsep kuantiti tak terhingga berkait rapat dengan konsep had.

Infinitesimal

Susulan a n dipanggil CM. Nikolsky. Kursus analisis matematik. Jilid 1. Moscow, 1983., Jika . Sebagai contoh, urutan nombor adalah sangat kecil.

Fungsi itu dipanggil sangat kecil di sekitar satu titik dipanggil 0 jika .

Fungsi itu dipanggil infinitesimal at infinitesi, Jika atau .

Juga infinitesimal ialah fungsi yang merupakan perbezaan antara fungsi dan hadnya, iaitu, jika , Itu f(dipanggil) − a = α( dipanggil) , .

Kuantiti besar yang tidak terhingga

Susulan a n dipanggil besar tak terhingga, Jika .

Fungsi itu dipanggil besar tidak terhingga di sekitar satu titik dipanggil 0 jika .

Fungsi itu dipanggil besar tak terhingga pada tak terhingga, Jika atau .

Dalam semua kes, infiniti di sebelah kanan kesaksamaan tersirat untuk mempunyai tanda tertentu (sama ada "tambah" atau "tolak"). Iaitu, sebagai contoh, fungsi dipanggil dosa dipanggil tidak besar tidak terhingga pada .

Sifat-sifat infinitely small and infinitely large

Perbandingan kuantiti tak terhingga

Bagaimana untuk membandingkan kuantiti tak terhingga?
Nisbah kuantiti tak terhingga membentuk apa yang dipanggil ketidakpastian.

Definisi

Katakan kita mempunyai nilai paling kecil α( dipanggil) dan β( dipanggil) (atau, yang tidak penting untuk definisi, jujukan sangat kecil).

Untuk mengira had sedemikian adalah mudah untuk menggunakan peraturan L'Hopital.

Contoh perbandingan

menggunakan TENTANG-simbolisme, keputusan yang diperolehi boleh ditulis dalam bentuk berikut dipanggil 5 = o(dipanggil 3). DALAM dalam kes ini rekod adalah betul 2dipanggil 2 + 6dipanggil = O(dipanggil) Dan dipanggil = O(2dipanggil 2 + 6dipanggil).

Nilai yang setara

Definisi

Jika , maka kuantiti tak terhingga α dan β dipanggil setara ().
Adalah jelas bahawa kuantiti yang setara adalah kes khas kuantiti tak terhingga dengan susunan kekecilan yang sama.

Apabila hubungan kesetaraan berikut adalah sah: , , .

Teorem

Had hasil bagi (nisbah) dua kuantiti tak terhingga tidak akan berubah jika salah satu daripadanya (atau kedua-duanya) digantikan dengan kuantiti yang setara.

Teorem ini mempunyai kepentingan praktikal apabila mencari had (lihat contoh).

Contoh penggunaan

Menggantikan sin 2dipanggil nilai setara 2 dipanggil, kita dapat

Lakaran sejarah

Konsep "infinitesimal" telah dibincangkan pada zaman dahulu berkaitan dengan konsep atom tidak boleh dibahagikan, tetapi tidak termasuk dalam matematik klasik. Ia dihidupkan semula dengan kemunculan "kaedah tidak boleh dibahagikan" pada abad ke-16 - membahagikan angka yang dikaji kepada bahagian yang sangat kecil.

Pada abad ke-17, algebraisasi kalkulus infinitesimal berlaku. Ia mula ditakrifkan sebagai kuantiti berangka yang kurang daripada mana-mana kuantiti terhingga (bukan sifar) tetapi tidak sama dengan sifar. Seni analisis terdiri daripada merangka hubungan yang mengandungi infinitesimal (pembezaan) dan kemudian mengintegrasikannya.

Ahli matematik sekolah lama menguji konsep itu sangat kecil kritikan yang pedas. Michel Rolle menulis bahawa kalkulus baharu ialah “ set kesilapan yang bijak"; Voltaire dengan tegas menyatakan bahawa kalkulus ialah seni mengira dan mengukur dengan tepat sesuatu yang kewujudannya tidak dapat dibuktikan. Malah Huygens mengakui bahawa dia tidak memahami maksud pembezaan perintah yang lebih tinggi.

Sebagai ironi nasib, seseorang boleh mempertimbangkan kemunculan analisis tidak standard pada pertengahan abad, yang membuktikan bahawa sudut pandangan asal - infinitesimal sebenar - juga konsisten dan boleh digunakan sebagai asas untuk analisis.

Lihat juga

Yayasan Wikimedia.

2010.

Lihat apa yang "Besar tak terhingga" dalam kamus lain: Kuantiti pembolehubah Y ialah songsangan bagi kuantiti tak terhingga X, iaitu, Y = 1/X...

Kamus Ensiklopedia Besar Pembolehubah y ialah songsangan bagi x terhingga, iaitu, y = 1/x. * * * BESAR TAK TERHINGGA BESAR TAK TERHINGGA, kuantiti berubah Y, songsang kepada kuantiti tak terhingga X, iaitu Y = 1/X ...

Kamus Ensiklopedia Dalam matematik, kuantiti pembolehubah yang, dalam proses perubahan tertentu, menjadi dan kekal lebih besar dalam nilai mutlak daripada sebarang nombor yang telah ditetapkan. Kajian B. b. kuantiti boleh dikurangkan kepada kajian infinitesimal (Lihat... ...

Ensiklopedia Soviet yang Hebat

Kemudian untuk semua orang, Sastera terpakai: L.D. Kudryavtsev. Kursus analisis matematik. Jilid 1. Moscow, 2003. FUNGSI INFINITESMALL DAN SIFAT ASASNYA Lihat juga: Fungsi y=f(x) dipanggil sangat kecil

atau bila

Marilah kita mewujudkan hubungan penting berikut:

Teorem. Jika fungsi Sastera terpakai:→∞, jika atau , i.e. fungsi infinitesimal ialah fungsi yang hadnya pada titik tertentu ialah sifar. Fungsi sebagai hasil tambah nombor tetap b boleh diwakili dengan α(x): f (x)=b+ α(x) dan magnitud tak terhingga

itu. f (x)=b+α(x) Sebaliknya, jika , maka a(x), Di mana x→a.

Bukti.

– sangat kecil pada

Teorem 1. Mari kita pertimbangkan sifat asas bagi fungsi infinitesimal.

Bukti Jumlah algebra bagi dua, tiga, dan secara amnya sebarang nombor terhingga bagi infinitesimal ialah fungsi infinitesimal. f(x)=α(x)+β(x). Mari kita berikan bukti untuk dua penggal. biarlah > , di mana dan . Kita perlu membuktikan bahawa untuk ε sewenang-wenangnya sewenang-wenangnya kecil δ> 0 ditemui dipanggil 0, supaya untuk |x – a|<δ , dilaksanakan |f(x)|< ε.

, memuaskan ketidaksamaan > 0. Oleh kerana mengikut syarat teorem α(x) Jadi, mari betulkan nombor arbitrari ε > ialah fungsi yang sangat kecil, maka terdapat δ 1 |x – a|< δ 1 kita ada |α(x)|< ε / 2. Begitu juga, sejak β(x) 0, iaitu > ialah fungsi yang sangat kecil, maka terdapat δ 1 |x – a|< δ 2 kita ada | β(x)|< ε / 2.

Mari ambil δ=min(δ 1 , δ2 } .Kemudian di kawasan kejiranan titik a jejari δ adalah sangat kecil, maka terdapat δ 2 |α(x)|< ε / 2 dan | β(x)|< ε / 2. setiap ketidaksamaan akan dipenuhi

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

mereka. |f(x)|< ε, itulah yang perlu dibuktikan.

Teorem 2. Hasil darab fungsi yang sangat kecil a(x) untuk fungsi terhad →∞, jika atau , i.e. tanpa henti di Fungsi(atau bila x→∞) ialah fungsi yang sangat kecil.

Daripada teorem terbukti ia berikut:

Akibat 1. Jika dan, maka.

Akibat 2. Jika dan c= const, kemudian .

Teorem 3. Nisbah fungsi infinitesimal α(x) setiap fungsi →∞, jika atau , i.e. tanpa henti, yang hadnya berbeza daripada sifar, ialah fungsi yang sangat kecil.

Bukti. biarlah . Kemudian 1 /f(x) terdapat fungsi terhad. Oleh itu pecahan ialah hasil darab fungsi tak terhingga dan fungsi terhad, i.e. fungsi adalah sangat kecil.

HUBUNGAN ANTARA FUNGSI KECIL DAN BESAR TAK TERHINGGA

Teorem 1. Jika fungsi →∞, jika atau , i.e. tanpa henti adalah besar tidak terhingga pada Fungsi, kemudian fungsi 1 /f(x) adalah sangat kecil pada Fungsi.

Bukti. Mari kita ambil nombor sewenang-wenangnya ε >0 dan tunjukkan itu untuk sesetengah orang δ>0 (bergantung kepada ε) untuk semua dipanggil, yang mana |x – a|<δ , ketidaksamaan itu berpuas hati, dan ini bermakna 1/f(x) ialah fungsi infinitesimal. Memang sejak →∞, jika atau , i.e. tanpa henti ialah fungsi yang tidak terhingga besar di Fungsi, maka akan ada δ>0 supaya sebaik sahaja |x – a|<δ , jadi | f(x)|> 1/ ε. Tetapi kemudian untuk perkara yang sama dipanggil.

atau bila

Teorem songsang juga boleh dibuktikan.

Teorem 2. Jika fungsi →∞, jika atau , i.e. tanpa henti- sangat kecil pada Fungsi(atau x→∞) dan tidak lenyap, maka y= 1/f(x) adalah fungsi yang tidak terhingga besar.

Jalankan pembuktian teorem itu sendiri.

atau bila

Oleh itu, sifat termudah bagi fungsi tak terhingga dan besar tak terhingga boleh ditulis menggunakan hubungan bersyarat berikut: A≠ 0

HAD TEOREMA

Teorem 1. Had jumlah algebra dua, tiga, dan secara amnya bilangan fungsi tertentu adalah sama dengan jumlah algebra had fungsi ini, i.e.

Bukti. Marilah kita melaksanakan pembuktian untuk dua penggal, kerana ia boleh dilakukan dengan cara yang sama untuk sebarang bilangan penggal. biarlah .Kemudian f(x)=b+α(x) Dan g(x)=c+β(x) Sebaliknya, jika , maka α Dan β – fungsi yang sangat kecil. Oleh itu,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Kerana b+c ialah pemalar, dan α(x) + β(x) ialah fungsi infinitesimal, maka

Contoh. .

Teorem 2. Had hasil darab dua, tiga, dan secara amnya bilangan terhingga fungsi adalah sama dengan hasil darab bagi had fungsi ini:

Bukti. biarlah . Oleh itu, f(x)=b+α(x) Dan g(x)=c+β(x) Dan

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Kerja bc terdapat nilai tetap. Fungsi bβ + c α + αβ berdasarkan sifat-sifat fungsi infinitesimal, terdapat kuantiti infinitesimal. sebab tu .

Akibat 1. Faktor malar boleh diambil melebihi tanda had:

Akibat 2. Had darjah sama dengan kuasa had:

Contoh..

Teorem 3. Had hasil bagi dua fungsi adalah sama dengan hasil bagi had fungsi ini jika had penyebut berbeza daripada sifar, i.e.

Bukti. biarlah . Oleh itu, f(x)=b+α(x) Dan g(x)=c+β(x), Di mana α, β – sangat kecil. Mari kita pertimbangkan hasil bagi

Pecahan ialah fungsi infinitesimal kerana pengangka ialah fungsi infinitesimal dan penyebutnya mempunyai had. c 2 ≠0.

atau bila

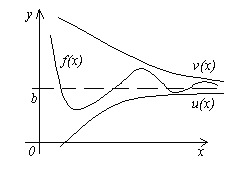
Teorem 4. Biar tiga fungsi diberikan f(x), u(x) Dan v(x), memuaskan ketidaksamaan u (x)≤f(x)≤ v(x). Jika fungsi u(x) Dan v(x) mempunyai had yang sama di Fungsi(atau x→∞), kemudian fungsi →∞, jika atau , i.e. tanpa henti cenderung kepada had yang sama, i.e. Jika

, Itu .

Maksud teorem ini jelas daripada rajah.

Bukti Teorem 4 boleh didapati, sebagai contoh, dalam buku teks: Piskunov N. S. Kalkulus pembezaan dan kamiran, jilid 1 - M.: Nauka, 1985.

Teorem 5. Jika di Fungsi(atau x→∞) fungsi Sastera terpakai: menerima nilai bukan negatif y≥0 dan pada masa yang sama cenderung kepada had b, maka had ini tidak boleh negatif: b≥0.

Bukti. Kami akan melaksanakan pembuktian dengan percanggahan. Mari kita anggap itu b<0 , Kemudian |y – b|≥|b| dan, oleh itu, modulus perbezaan tidak cenderung kepada sifar apabila Fungsi. Tetapi kemudian y tidak mencapai had b Lihat juga: Fungsi, yang bercanggah dengan syarat teorem.

Teorem 6. Jika dua fungsi →∞, jika atau , i.e. tanpa henti Dan g(x) untuk semua nilai hujah dipanggil memuaskan ketidaksamaan f(x)≥ g(x) dan mempunyai had, maka ketidaksamaan itu berlaku b≥c.

Bukti. Mengikut syarat teorem f(x)-g(x) ≥0, oleh itu, oleh Teorem 5 , atau .

HAD UNILAT

Setakat ini kita telah mempertimbangkan untuk menentukan had fungsi apabila Fungsi dengan cara sewenang-wenangnya, i.e. had fungsi tidak bergantung pada bagaimana ia terletak dipanggil berhubung dengan a, ke kiri atau kanan a. Walau bagaimanapun, adalah perkara biasa untuk mencari fungsi yang tidak mempunyai had di bawah syarat ini, tetapi mereka mempunyai had jika Fungsi, kekal di sebelah A, kiri atau kanan (lihat rajah). Oleh itu, konsep had berat sebelah diperkenalkan.

Jika →∞, jika atau , i.e. tanpa henti cenderung kepada had b Lihat juga: dipanggil cenderung kepada nombor tertentu a Jadi dipanggil hanya menerima nilai kurang daripada a, kemudian mereka menulis dan memanggil blimit fungsi f(x) pada titik a di sebelah kiri.

Kalkulus infinitesimal dan larges

kalkulus infinitesimal- pengiraan yang dilakukan dengan kuantiti tak terhingga, di mana hasil terbitan dianggap sebagai jumlah tak terhingga bagi infinite. Kalkulus infinitesimals ialah konsep umum untuk kalkulus pembezaan dan kamiran, yang menjadi asas kepada matematik moden yang lebih tinggi. Konsep kuantiti tak terhingga berkait rapat dengan konsep had.

Infinitesimal

Susulan a n dipanggil CM. Nikolsky. Kursus analisis matematik. Jilid 1. Moscow, 1983., Jika . Sebagai contoh, urutan nombor adalah sangat kecil.

Fungsi itu dipanggil sangat kecil di sekitar satu titik dipanggil 0 jika .

Fungsi itu dipanggil infinitesimal at infinitesi, Jika atau .

Juga infinitesimal ialah fungsi yang merupakan perbezaan antara fungsi dan hadnya, iaitu, jika , Itu f(dipanggil) − a = α( dipanggil) , .

Kuantiti besar yang tidak terhingga

Dalam semua formula di bawah, infiniti di sebelah kanan kesaksamaan tersirat untuk mempunyai tanda tertentu (sama ada "tambah" atau "tolak"). Iaitu, sebagai contoh, fungsi dipanggil dosa dipanggil, tidak terhad pada kedua-dua belah, tidak besar terhingga pada .

Susulan a n dipanggil besar tak terhingga, Jika .

Fungsi itu dipanggil besar tidak terhingga di sekitar satu titik dipanggil 0 jika .

Fungsi itu dipanggil besar tak terhingga pada tak terhingga, Jika atau .

Sifat-sifat infinitely small and infinitely large

Perbandingan kuantiti tak terhingga

Bagaimana untuk membandingkan kuantiti tak terhingga?
Nisbah kuantiti tak terhingga membentuk apa yang dipanggil ketidakpastian.

Definisi

Katakan kita mempunyai nilai paling kecil α( dipanggil) dan β( dipanggil) (atau, yang tidak penting untuk definisi, jujukan sangat kecil).

Untuk mengira had sedemikian adalah mudah untuk menggunakan peraturan L'Hopital.

Contoh perbandingan

menggunakan TENTANG-simbolisme, keputusan yang diperolehi boleh ditulis dalam bentuk berikut dipanggil 5 = o(dipanggil 3). Dalam kes ini, entri berikut adalah benar: 2dipanggil 2 + 6dipanggil = O(dipanggil) Dan dipanggil = O(2dipanggil 2 + 6dipanggil).

Nilai yang setara

Definisi

Jika , maka kuantiti tak terhingga α dan β dipanggil setara ().
Adalah jelas bahawa kuantiti yang setara adalah kes khas kuantiti tak terhingga dengan susunan kekecilan yang sama.

Apabila hubungan kesetaraan berikut adalah sah (sebagai akibat daripada apa yang dipanggil had luar biasa):

Teorem

Had hasil bagi (nisbah) dua kuantiti tak terhingga tidak akan berubah jika salah satu daripadanya (atau kedua-duanya) digantikan dengan kuantiti yang setara.

Teorem ini mempunyai kepentingan praktikal apabila mencari had (lihat contoh).

Contoh penggunaan

Menggantikan sin 2dipanggil nilai setara 2 dipanggil, kita dapat

Lakaran sejarah

Lihat juga

Yayasan Wikimedia.

Lihat apa "Kuantiti Infinitesimal" dalam kamus lain:

KUANTITI TAK TERHINGGA KECIL- kuantiti berubah dalam proses tertentu, jika dalam proses ini ia menghampiri (cenderung) kepada sifar secara tak terhingga... Ensiklopedia Politeknik Besar

Infinitesimal- ■ Sesuatu yang tidak diketahui, tetapi berkaitan dengan homeopati... Leksikon kebenaran umum

Bahagian