Хязгааргүй том функцууд нь тэдний шинж чанар юм. Хязгааргүй том функцийн тодорхойлолт. Хязгааргүй жижиг функцууд

Хязгааргүй том дарааллын тодорхойлолтыг өгсөн болно. Хязгааргүй алслагдсан цэгүүдийн хөршүүдийн тухай ойлголтыг авч үздэг. Дарааллын хязгаарын бүх нийтийн тодорхойлолтыг өгсөн бөгөөд энэ нь төгсгөлтэй болон хязгааргүй хязгаарт хамаарна. Хязгааргүй том дарааллын тодорхойлолтыг хэрэглэх жишээг авч үзнэ.

Агуулга

Мөн үзнэ үү: Дарааллын хязгаарыг тодорхойлох

Тодорхойлолт

Дараалал (βn) хязгааргүй дараалал гэж нэрлэдэг, хэрвээ дурын олон тооны M-ийн хувьд ийм байдаг натурал тооБүх эерэг бүхэл тоонуудын хувьд n > N M тэгш бус байдал байхаар M-ээс хамаарч N M байна
|β n | >М.
Энэ тохиолдолд бичнэ үү
.
Эсвэл цагт.
Тэд энэ нь хязгааргүй хандлагатай гэж хэлдэг, эсвэл хязгааргүйд нийлдэг.

Хэрэв , N тооноос эхлэн 0 , дараа нь
( нэмэх хязгаарт нийлдэг).
Хэрэв бол
( хасах хязгааргүйд нийлдэг).

Бид эдгээр тодорхойлолтыг оршин тогтнох, түгээмэл байдлын логик тэмдгүүдийг ашиглан бичдэг.
(1) .
(2) .
(3) .

(2) ба (3) хязгаартай дараалал нь хязгааргүй том дарааллын (1) онцгой тохиолдол юм. Эдгээр тодорхойлолтоос харахад дарааллын хязгаар нь нэмэх эсвэл хасах хязгааргүй бол энэ нь мөн адил хязгааргүйтэй тэнцүү байна:
.
Урвуу нь мэдээжийн хэрэг үнэн биш юм. Дарааллын гишүүд ээлжлэн тэмдэгтүүдтэй байж болно. Энэ тохиолдолд хязгаар нь хязгааргүйтэй тэнцүү боловч тодорхой тэмдэггүй байж болно.

Хэрэв тодорхой шинж чанар нь хязгаартай тэнцүү хязгаартай дурын дараалалд тохирч байвал хязгаар нь нэмэх эсвэл хасах хязгааргүй дараалалд ижил шинж чанар хамаарна гэдгийг анхаарна уу.

Тооцооллын олон сурах бичигт хязгааргүй том дарааллын тодорхойлолтод M тоог эерэг гэж заасан байдаг: M. > 0 . Гэсэн хэдий ч энэ шаардлага нь илүүц юм. Хэрэв үүнийг цуцалсан бол зөрчилдөөн гарахгүй. Зөвхөн жижиг эсвэл сөрөг үнэ цэнэ нь бидний сонирхлыг татдаггүй. Бид M-ийн дур зоргоороо том эерэг утгуудын дарааллын зан үйлийг сонирхож байна. Иймд шаардлага гарвал М-г доороос ямар ч өгөгдсөн a тоогоор хязгаарлаж болно, өөрөөр хэлбэл M > a гэж үзье.

Бид ε - төгсгөлийн цэгийн хөршийг тодорхойлохдоо ε шаардлага тавина > 0 чухал юм. Сөрөг утгын хувьд тэгш бус байдал нь огтхон ч байж чадахгүй.

Хязгааргүй цэгүүдийн хөршүүд

Хязгаарлагдмал хязгаарыг авч үзэхдээ бид цэгийн ойр орчмын тухай ойлголтыг оруулсан. Төгсгөлийн цэгийн хөрш нь энэ цэгийг агуулсан нээлттэй интервал гэдгийг санаарай. Мөн бид хязгааргүй дэх цэгүүдийн хөршийн тухай ойлголтыг танилцуулж болно.

M нь дурын тоо байг.
"Хязгааргүй" цэгийн хөрш, , олонлог гэж нэрлэдэг.
"нэмэх хязгааргүй" цэгийн хөрш, , олонлог гэж нэрлэдэг.
"Хязгааргүйг хасах" цэгийн хөрш, , олонлог гэж нэрлэдэг.

Хатуухан хэлэхэд "хязгааргүй" цэгийн хөрш нь олонлог юм
(4) ,
хаана М 1 болон М 2 дурын эерэг тоонууд. Бид эхний тодорхойлолтыг ашиглах болно, учир нь энэ нь илүү хялбар байдаг. Хэдийгээр (4) тодорхойлолтыг ашиглах үед доор дурдсан бүх зүйл үнэн болно.

Одоо бид төгсгөлтэй болон хязгааргүй хязгаарт хамаарах дарааллын хязгаарын нэгдсэн тодорхойлолтыг өгч чадна.

Дарааллын хязгаарын бүх нийтийн тодорхойлолт.
Хэрэв энэ цэгийн аль ч орчимд тоо бүхий дарааллын бүх элементүүд энэ тойрогт хамаарах тийм натурал N тоо байвал a цэг (хязгааргүй эсвэл хязгааргүй) нь дарааллын хязгаар юм.

Тиймээс хэрэв хязгаар байгаа бол а цэгийн хөршөөс гадна дарааллын зөвхөн хязгаарлагдмал тооны гишүүд эсвэл хоосон олонлог байж болно. Энэ нөхцөл шаардлагатай бөгөөд хангалттай. Энэ өмчийн баталгаа нь хязгаарлагдмал хязгаартай яг адилхан юм.

Нийлмэл дарааллын хөршийн шинж чанар
А цэг (хязгааргүй эсвэл хязгааргүй) дарааллын хязгаар байхын тулд энэ цэгийн аль ч орчмын гадна дарааллын хязгаарлагдмал тооны гишүүд эсвэл хоосон олонлог байх шаардлагатай бөгөөд хангалттай.
Баталгаа.

Түүнчлэн, ε - хязгааргүй алслагдсан цэгүүдийн хөршүүдийн тухай ойлголтыг заримдаа нэвтрүүлдэг.
Төгсгөлийн а цэгийн ε - хөрш олонлог гэдгийг санаарай.
Ингээд танилцуулъя дараах тэмдэглэгээ. a цэгийн ε - хөршийг илэрхийлье. Дараа нь эцсийн цэгийн хувьд,
.
Хязгааргүй цэгийн хувьд:
;
;
.
ε - хөршүүдийн ойлголтыг ашиглан дарааллын хязгаарын өөр нэг нийтлэг тодорхойлолтыг өгч болно.

a цэг (хязгааргүй эсвэл хязгааргүй) нь хэрэв байгаа бол дарааллын хязгаар юм эерэг тоо ε > 0 бүх n > N ε тоонуудын хувьд x n гишүүд нь a цэгийн ε хөршид хамаарах тул ε-ээс хамаарсан N ε натурал тоо байдаг:
.

Оршихуй ба түгээмэл байдлын логик тэмдгүүдийг ашиглан энэхүү тодорхойлолтыг дараах байдлаар бичиж болно.
.

Хязгааргүй том дарааллын жишээ

Жишээ 1

.

.
Бид хязгааргүй том дарааллын тодорхойлолтыг бичнэ.
(1) .
Манай тохиолдолд
.

Бид тоонуудыг танилцуулж, тэдгээрийг тэгш бус байдалтай холбоно.
.
Тэгш бус байдлын шинж чанарын дагуу , хэрэв ба , тэгвэл
.
Энэ тэгш бус байдал ямар ч n-д биелэхийг анхаарна уу. Тиймээс та дараах байдлаар сонгож болно.
үед;
цагт.

Тиймээс хэн ч тэгш бус байдлыг хангах натурал тоог олж чадна. Дараа нь бүгдэд нь
.
гэсэн үг. Энэ нь дараалал нь хязгааргүй том юм.

Жишээ 2

Хязгааргүй том дарааллын тодорхойлолтыг ашиглан үүнийг харуул
.

(2) .
Өгөгдсөн дарааллын нийтлэг нэр томъёо нь дараах хэлбэртэй байна.
.

Тоонуудыг оруулаад:
.
.

Дараа нь хэн ч тэгш бус байдлыг хангадаг натурал тоог олох боломжтой бөгөөд ингэснээр бүгдэд нь,
.
гэсэн үг.

.

Жишээ 3

Хязгааргүй том дарааллын тодорхойлолтыг ашиглан үүнийг харуул
.

Хасах хязгаартай тэнцүү дарааллын хязгаарын тодорхойлолтыг бичье.
(3) .
Өгөгдсөн дарааллын нийтлэг нэр томъёо нь дараах хэлбэртэй байна.
.

Тоонуудыг оруулаад:
.
Энэ нь хэрэв ба, дараа нь гэдгийг харуулж байна
.

Учир нь хэн ч тэгш бус байдлыг хангах натурал тоог олох боломжтой
.

N гэж өгөгдсөн бол та дараах тэгш бус байдлыг хангасан дурын натурал тоог авч болно.
.

Жишээ 4

Хязгааргүй том дарааллын тодорхойлолтыг ашиглан үүнийг харуул
.

Дарааллын нийтлэг гишүүнийг бичье.
.
Хязгааргүй нэмэхтэй тэнцүү дарааллын хязгаарын тодорхойлолтыг бичье.
(2) .

n нь натурал тоо тул n = 1, 2, 3, ... , дараа нь
;
;
.

Бид тоонууд ба M-ийг танилцуулж, тэдгээрийг тэгш бус байдлаар холбоно.
.
Энэ нь хэрэв ба, дараа нь гэдгийг харуулж байна
.

Тиймээс ямар ч M тооны хувьд тэгш бус байдлыг хангах натурал тоог олж болно. Дараа нь бүгдэд нь
.
гэсэн үг.

Лавлагаа:
Л.Д. Кудрявцев. Математик анализын курс. 1-р боть. Москва, 2003 он.
CM. Никольский. Математик анализын курс. 1-р боть. Москва, 1983 он.

Мөн үзнэ үү:

Чиг үүрэг y=f(x)дуудсан хязгааргүй жижигцагт x→aэсвэл хэзээ x→∞ хэрэв эсвэл , i.e. Өгөгдсөн цэг дэх хязгаар нь тэг байх функцийг хязгааргүй жижиг функц гэнэ.

Жишээ.

1. Үйл ажиллагаа f(x)=(x-1) 2 нь хязгааргүй жижиг x→1, оноос хойш (Зураг харна уу).

2. Үйл ажиллагаа f(x)=тг xүед хязгааргүй жижиг байна x→0.

3. f(x)= бүртгэл(1+ x) -д хязгааргүй жижиг байна x→0.

4. f(x) = 1/xүед хязгааргүй жижиг байна x→∞.

Дараах чухал харилцааг тогтооцгооё.

Теорем.Хэрэв функц y=f(x)хаягаар төлөөлөх боломжтой x→aтогтмол тооны нийлбэр байдлаар бмөн хязгааргүй жижиг α(x): f(x)=b+ α(x)дараа нь.

Харин эсрэгээр, хэрэв , тэгвэл f(x)=b+α(x), хаана a(x)үед хязгааргүй жижиг байна x→a.

Баталгаа.

1. Батламжийн эхний хэсгийг баталъя. Тэгш эрхээс f(x)=b+α(x)ёстой |f(x) – b|=| α|. Гэхдээ түүнээс хойш a(x)нь хязгааргүй жижиг бол дурын ε-ийн хувьд δ, цэгийн хөрш байна. а,бүгдэд нь xүүнээс, үнэт зүйлс a(x)харилцааг хангана |α(x)|< ε. Дараа нь |f(x) – b|< ε. Мөн энэ нь гэсэн үг юм.

2. Хэрэв ε-ийн хувьд бол >0 бүгдэд нь X from some δ нь тухайн цэгийн хөрш юм абайх болно |f(x) – b|< ε. Гэхдээ хэрэв бид тэмдэглэвэл f(x) – b= α, дараа нь |α(x)|< ε гэсэн үг а- хязгааргүй жижиг.

Хязгааргүй жижиг функцүүдийн үндсэн шинж чанаруудыг авч үзье.

Теорем 1.Хоёр, гурав, ерөнхийдөө дурын төгсгөлтэй тооны хязгааргүй жижиг тоонуудын алгебрийн нийлбэр нь хязгааргүй жижиг функц юм.

Баталгаа. Хоёр нөхцлийн нотолгоо өгье. Болъё f(x)=α(x)+β(x), хаана болон . Дурын дурын жижиг ε-ийн хувьд бид үүнийг батлах хэрэгтэй > 0 тэнд δ> 0, үүний төлөө xтэгш бус байдлыг хангаж байна |x – a|<δ , гүйцэтгэсэн |f(x)|< ε.

Тиймээс бид дурын ε тоог засдаг > 0. Учир нь теоремын таамаглалын дагуу. α(x)нь хязгааргүй жижиг функц бол δ 1 байна > 0, аль нь |x – a|< δ 1 бидэнд байна |α(x)|< ε / 2. Үүний нэгэн адил, оноос хойш β(x)хязгааргүй жижиг бол ийм δ 2 байна > 0, аль нь |x – a|< δ 2 бидэнд байна | β(x)|< ε / 2.

Авцгаая δ=мин(δ1 , δ2 } .Дараа нь тухайн цэгийн ойр орчимд арадиус δ тэгш бус байдал бүрийг хангана |α(x)|< ε / 2 ба | β(x)|< ε / 2. Тиймээс энэ хороололд байх болно

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

тэдгээр. |f(x)|< нотлох ёстой байсан ε.

Теорем 2.Хязгааргүй жижиг функцийн бүтээгдэхүүн a(x)хязгаарлагдмал функцэд зориулагдсан f(x)цагт x→a(эсвэл хэзээ x→∞) нь хязгааргүй жижиг функц юм.

Баталгаа. Функцээс хойш f(x)хязгаарлагдмал, дараа нь тоо байна Мбүх үнэт зүйлсийн хувьд xцэгийн зарим хөршөөс a|f(x)|≤M.Үүнээс гадна, оноос хойш a(x)нь хязгааргүй жижиг функц юм x→a, дараа нь дурын ε-ийн хувьд > 0 цэгийн хөрш байдаг а, үүнд тэгш бус байдал |α(x)|< ε /М. Дараа нь эдгээр жижиг хороололд бид байдаг | αf|< ε /М= ε. Мөн энэ нь тийм гэсэн үг юм af- хязгааргүй жижиг. Хэргийн хувьд x→∞нотлох баримт нь ижил төстэй байдлаар хийгддэг.

Батлагдсан теоремоос дараах байдалтай байна.

Үр дагавар 1.Хэрэв ба бол .

Үр дагавар 2.Хэрэв ба c= const, дараа нь .

Теорем 3.Хязгааргүй жижиг функцийн харьцаа α(x)функц бүрт f(x), хязгаар нь тэгээс ялгаатай нь хязгааргүй жижиг функц юм.

Баталгаа. Let . Дараа нь 1 /f(x)хязгаарлагдмал функц байдаг. Тиймээс бутархай нь хязгааргүй жижиг функц ба хязгаарлагдмал функцийн үржвэр юм, i.e. функц нь хязгааргүй жижиг.

Хязгааргүй жижиг ба том тоонуудын тооцоо

Хязгааргүй жижиг тооцоо- үүсмэл үр дүнг хязгааргүй жижиг утгуудын хязгааргүй нийлбэр гэж үздэг хязгааргүй жижиг утгуудаар хийсэн тооцоолол. Хязгааргүй жижиг тооллын тооцоо нь орчин үеийн дээд математикийн үндэс болсон дифференциал ба интеграл тооцооллын ерөнхий ойлголт юм. Хязгааргүй хэмжигдэхүүний тухай ойлголт нь хязгаарын тухай ойлголттой нягт холбоотой.

Хязгааргүй жижиг

Дараалал а nдуудсан хязгааргүй жижиг, хэрэв . Жишээлбэл, тоонуудын дараалал нь хязгааргүй бага байдаг.

Функцийг дууддаг цэгийн ойролцоо хязгааргүй жижиг x 0 бол .

Функцийг дууддаг хязгааргүй жижиг, хэрэв эсвэл .

Мөн хязгааргүй жижиг функц нь функц ба түүний хязгаарын ялгаа, өөрөөр хэлбэл хэрэв , дараа нь е(x) − а = α( x) , .

хязгааргүй том

Дараалал а nдуудсан хязгааргүй том, хэрэв .

Функцийг дууддаг цэгийн ойролцоо хязгааргүй том x 0 бол .

Функцийг дууддаг хязгааргүйд хязгааргүй том, хэрэв эсвэл .

Бүх тохиолдолд тэгш эрхийн хязгааргүй байдал нь тодорхой тэмдэгтэй ("нэмэх" эсвэл "хасах") байна гэж үздэг. Энэ нь жишээлбэл, функц юм xнүгэл x-ийн хувьд хязгааргүй том биш юм.

Хязгааргүй ба хязгааргүй жижиг тоонуудын шинж чанарууд

Хязгааргүй жижиг тоонуудын харьцуулалт

Хязгааргүй жижиг хэмжигдэхүүнүүдийг хэрхэн харьцуулах вэ?
Хязгааргүй жижиг хэмжигдэхүүнүүдийн харьцаа нь тодорхойгүй байдлыг үүсгэдэг.

Тодорхойлолт

Ижил утгын хувьд бид хязгааргүй бага байна гэж бодъё α( x) ба β( x) (эсвэл тодорхойлолтод чухал биш, хязгааргүй жижиг дараалал).

Ийм хязгаарыг тооцоолохын тулд L'Hospital-ийн дүрмийг ашиглах нь тохиромжтой.

Харьцуулах жишээ

Ашиглаж байна О-гарсан үр дүнгийн тэмдэглэгээг дараах хэлбэрээр бичиж болно x 5 = о(x 3). AT Энэ тохиолдолдбүртгэл үнэн 2x 2 + 6x = О(x) болон x = О(2x 2 + 6x).

Тэнцүү хэмжигдэхүүнүүд

Тодорхойлолт

Хэрэв бол α ба β хязгааргүй жижиг хэмжигдэхүүнүүдийг дуудна тэнцүү ().
Мэдээжийн хэрэг, эквивалент хэмжигдэхүүн нь ижил жижиг дарааллын хязгааргүй жижиг хэмжигдэхүүнүүдийн онцгой тохиолдол юм.

-ийн хувьд дараах эквивалент хамаарал хүчинтэй байна: , , .

Теорем

Хоёр хязгааргүй жижиг хэмжигдэхүүний (харьцаа) хязгаар нь тэдгээрийн аль нэгийг (эсвэл хоёуланг нь) эквивалент утгаар сольсон тохиолдолд өөрчлөгдөхгүй..

Энэ теорем нь хязгаарыг олоход практик ач холбогдолтой (жишээг үзнэ үү).

Хэрэглээний жишээ

Солих сбиn 2x эквивалент утга 2 x, бид авдаг

Түүхэн тойм

"Хязгааргүй жижиг" гэсэн ойлголтыг эрт дээр үед хуваагдашгүй атомын тухай ойлголттой холбон ярьж байсан ч сонгодог математикт орж ирээгүй. Дахин хэлэхэд энэ нь 16-р зуунд "хуваагдах арга" гарч ирснээр дахин сэргэсэн - судалж буй дүрсийг хязгааргүй жижиг хэсгүүдэд хуваах.

Хязгааргүй жижиг тооцооллын алгебрчлал 17-р зуунд болсон. Тэдгээрийг ямар ч төгсгөлтэй (тэг биш) утгаас бага боловч тэгтэй тэнцүү биш тоон утгууд гэж тодорхойлж эхэлсэн. Шинжилгээний урлаг нь хязгааргүй жижиг тоо (дифференциал) агуулсан харилцааг зохиож, дараа нь түүнийг нэгтгэх явдал байв.

Хуучин сургуулийн математикчид энэ үзэл баримтлалд хамрагдсан хязгааргүй жижигхатуу шүүмжлэл. Мишель Ролле шинэ тооцоо бол " гайхалтай алдаануудын багц»; Вольтер энэхүү тооцоолол нь оршин тогтнох нь нотлогдох боломжгүй зүйлсийг тооцоолох, нарийн хэмжих урлаг юм гэж хор хөнөөлтэй онцолсон. Гюйгенс хүртэл дээд эрэмбийн дифференциалын утгыг ойлгоогүй гэдгээ хүлээн зөвшөөрсөн.

Хувь заяаны инээдэм болгон зууны дунд үеийн стандарт бус шинжилгээний дүр төрхийг авч үзэх боломжтой бөгөөд энэ нь анхны үзэл бодол - бодит хязгаарлагдмал тоо баримт нь нийцэж байгааг нотолсон бөгөөд дүн шинжилгээ хийх үндэс болгон авч болно.

бас үзнэ үү

Викимедиа сан. 2010 он.

Бусад толь бичгүүдээс "Хязгааргүй том" гэж юу болохыг хараарай:

Хязгааргүй X-ийн эсрэг утгатай Y хувьсагч, өөрөөр хэлбэл Y = 1/X... Том нэвтэрхий толь бичиг

Хязгааргүй х-ийн эсрэг утгатай y хувьсагч, өөрөөр хэлбэл y = 1/x. * * * ХЯЗГААРГҮЙ ТОМ ХЯЗГААРГҮЙ ТОМ, хувьсах утга Y, хязгааргүй бага утгын хариу X, өөрөөр хэлбэл, Y = 1/X ... нэвтэрхий толь бичиг

Математикийн хувьд өгөгдсөн өөрчлөлтийн явцад урьдчилан тодорхойлсон тооноос үнэмлэхүй утгаараа их болж, хэвээр байгаа хувьсагч юм. Б сурч байна. Хязгааргүй жижиг тоонуудыг судлахын тулд хэмжигдэхүүнийг багасгаж болно (... ... үзнэ үү. Зөвлөлтийн агуу нэвтэрхий толь бичиг

ХЯЗГААРГҮЙ ЖИЖИГ ҮЙЛ АЖИЛЛАГАА БА ТЭДНИЙ ҮНДСЭН ШИНЖ

Чиг үүрэг y=f(x)дуудсан хязгааргүй жижигцагт x→aэсвэл хэзээ x→∞ хэрэв эсвэл , i.e. Өгөгдсөн цэг дэх хязгаар нь тэг байх функцийг хязгааргүй жижиг функц гэнэ.

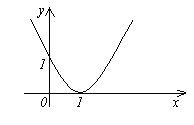
Жишээ.

Дараах чухал харилцааг тогтооцгооё.

Теорем.Хэрэв функц y=f(x)хаягаар төлөөлөх боломжтой x→aтогтмол тооны нийлбэр байдлаар бмөн хязгааргүй жижиг α(x): f(x)=b+ α(x)дараа нь.

Харин эсрэгээр, хэрэв , тэгвэл f(x)=b+α(x), хаана a(x)үед хязгааргүй жижиг байна x→a.

Баталгаа.

Хязгааргүй жижиг функцүүдийн үндсэн шинж чанаруудыг авч үзье.

Теорем 1.Хоёр, гурав, ерөнхийдөө дурын төгсгөлтэй тооны хязгааргүй жижиг тоонуудын алгебрийн нийлбэр нь хязгааргүй жижиг функц юм.

Баталгаа. Хоёр нөхцлийн нотолгоо өгье. Болъё f(x)=α(x)+β(x), хаана болон . Дурын дурын жижиг ε-ийн хувьд бид үүнийг батлах хэрэгтэй > 0 тэнд δ> 0, үүний төлөө xтэгш бус байдлыг хангаж байна |x – a|<δ , гүйцэтгэсэн |f(x)|< ε.

Тиймээс бид дурын ε тоог засдаг > 0. Учир нь теоремын таамаглалын дагуу. α(x)нь хязгааргүй жижиг функц бол δ 1 байна > 0, аль нь |x – a|< δ 1 бидэнд байна |α(x)|< ε / 2. Үүний нэгэн адил, оноос хойш β(x)хязгааргүй жижиг бол ийм δ 2 байна > 0, аль нь |x – a|< δ 2 бидэнд байна | β(x)|< ε / 2.

Авцгаая δ=мин(δ1 , δ2 } .Дараа нь тухайн цэгийн ойр орчимд арадиус δ тэгш бус байдал бүрийг хангана |α(x)|< ε / 2 ба | β(x)|< ε / 2. Тиймээс энэ хороололд байх болно

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

тэдгээр. |f(x)|< нотлох ёстой байсан ε.

Теорем 2.Хязгааргүй жижиг функцийн бүтээгдэхүүн a(x)хязгаарлагдмал функцэд зориулагдсан f(x)цагт x→a(эсвэл хэзээ x→∞) нь хязгааргүй жижиг функц юм.

Баталгаа. Функцээс хойш f(x)хязгаарлагдмал, дараа нь тоо байна Мбүх үнэт зүйлсийн хувьд xцэгийн зарим хөршөөс a|f(x)|≤M.Үүнээс гадна, оноос хойш a(x)нь хязгааргүй жижиг функц юм x→a, дараа нь дурын ε-ийн хувьд > 0 цэгийн хөрш байдаг а, үүнд тэгш бус байдал |α(x)|< ε /М. Дараа нь эдгээр жижиг хороололд бид байдаг | αf|< ε /М= ε. Мөн энэ нь тийм гэсэн үг юм af- хязгааргүй жижиг. Хэргийн хувьд x→∞нотлох баримт нь ижил төстэй байдлаар хийгддэг.

Батлагдсан теоремоос дараах байдалтай байна.

Үр дагавар 1.Хэрэв ба бол .

Үр дагавар 2.Хэрэв ба c= const, дараа нь .

Теорем 3.Хязгааргүй жижиг функцийн харьцаа α(x)функц бүрт f(x), хязгаар нь тэгээс ялгаатай нь хязгааргүй жижиг функц юм.

Баталгаа. Болъё . Дараа нь 1 /f(x)хязгаарлагдмал функц байдаг. Тиймээс бутархай нь хязгааргүй жижиг функц ба хязгаарлагдмал функцийн үржвэр юм, i.e. функц нь хязгааргүй жижиг юм.

ХЯЗГААРГҮЙ ЖИЖИГ, ХЯЗГААРГҮЙ ТОМ функцуудын ХАРИЛЦАА

Теорем 1.Хэрэв функц f(x)үед хязгааргүй том байна x→a, дараа нь функц 1 /f(x)үед хязгааргүй жижиг байна x→a.

Баталгаа.Дурын ε тоог ав >0 мөн заримд нь үүнийг харуул δ>0 (ε-ээс хамаарч) бүгдэд нь x, Үүний төлөө |x – a|<δ , тэгш бус байдал хангагдсан бөгөөд энэ нь гэсэн үг болно 1/f(x)нь хязгааргүй жижиг функц юм. Үнэхээр тэр цагаас хойш f(x)нь хязгааргүй том функц юм x→a, тэгвэл байна δ>0 тэр даруйдаа |x – a|<δ , тэгэхээр | f(x)|> 1/ ε. Гэхдээ дараа нь мөн адил x.

Жишээ.

Эсрэг теоремыг мөн баталж болно.

Теорем 2.Хэрэв функц f(x)- хязгааргүй жижиг at x→a(эсвэл x→∞)тэгээд алга болохгүй у= 1/f(x)нь хязгааргүй функц юм.

Теоремыг өөрөө батал.

Жишээ.

Ийнхүү хязгааргүй ба хязгааргүй жижиг тоонуудын хамгийн энгийн шинж чанарууд том функцуудДараах нөхцөлт харилцааг ашиглан бичиж болно. А≠ 0

Хязгаарын тухай ТЕОРЕМ

Теорем 1.Хоёр, гурав, ерөнхийдөө тодорхой тооны функцүүдийн алгебрийн нийлбэрийн хязгаар нь эдгээр функцүүдийн хязгаарын алгебрийн нийлбэртэй тэнцүү байна, i.e.

Баталгаа. Олон тооны нэр томъёоны хувьд энэ нь ижил аргаар явагддаг тул бид нотолгоог хоёр нэр томъёогоор гүйцэтгэнэ. Болъё .Дараа нь f(x)=b+α(x)болон g(x)=c+β(x), хаана α болон β нь хязгааргүй жижиг функцууд юм. Үүний үр дүнд,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Учир нь b+cтогтмол бөгөөд α(x) + β(x)нь хязгааргүй жижиг функц юм

Жишээ. .

Теорем 2.Хоёр, гурав, ерөнхийдөө хязгаарлагдмал тооны функцын үржвэрийн хязгаар нь эдгээр функцүүдийн хязгаарын үржвэртэй тэнцүү байна.

Баталгаа. Болъё . Үүний үр дүнд, f(x)=b+α(x)болон g(x)=c+β(x)болон

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Ажил МЭӨтогтмол утга юм. Чиг үүрэг bβ + cα + αβхязгааргүй жижиг функцүүдийн шинж чанаруудын үндсэн дээр хязгааргүй жижиг хэмжигдэхүүн байдаг. Тийм ч учраас .

Үр дагавар 1.Тогтмол хүчин зүйлийг хязгаарын тэмдэгээс гаргаж болно:

.

Үр дагавар 2.зэрэглэлийн хязгаар зэрэгтэй тэнцүү байнахязгаар:

.

Жишээ..

Теорем 3.Хэрэв хуваагчийн хязгаар тэгээс өөр байвал хоёр функцийн хуваалтын хязгаар нь эдгээр функцүүдийн хязгаарын хуваарьтай тэнцүү байна, өөрөөр хэлбэл.

.

Баталгаа. Let . Үүний үр дүнд, f(x)=b+α(x)болон g(x)=c+β(x), хаана α, β хязгааргүй жижиг. Хэмжилтийг авч үзье

Бутархай нь хязгааргүй жижиг функц бөгөөд хуваагч нь хязгаартай байдаг. c2 ≠0.

Жишээ.

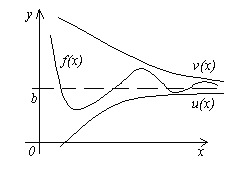
Теорем 4.Гурван функцийг өгье f(x), u(x)болон v(x), тэгш бус байдлыг хангах u (x)≤f(x)≤v(x). Хэрэв функцууд u(x)болон v(x)ижил хязгаартай x→a(эсвэл x→∞), дараа нь функц f(x)ижил хязгаарт хүрэх хандлагатай, i.e. хэрэв

, дараа нь.

Энэ теоремын утга нь зурагнаас тодорхой харагдаж байна.

Теорем 4-ийн нотолгоог жишээ нь сурах бичгээс олж болно: Пискунов Н.С. Дифференциал ба интегралын тооцоо, 1-р боть - М .: Наука, 1985.

Теорем 5.Хэрэв цагт x→a(эсвэл x→∞) функц y=f(x)сөрөг бус утгыг авдаг y≥0мөн хязгаарт хүрэх хандлагатай байдаг б, тэгвэл энэ хязгаар сөрөг байж болохгүй: b≥0.

Баталгаа. Нотлох баримтыг зөрчилдөөн хийх болно. Ингэж жүжиглэе б<0 , дараа нь |y – b|≥|b|ба иймээс ялгааны модуль нь тэг байх хандлагатай байдаггүй x→a. Харин дараа нь yхязгаарт хүрэхгүй бцагт x→a, энэ нь теоремын нөхцөлтэй зөрчилдөж байна.

Теорем 6.Хэрэв хоёр функц байвал f(x)болон g(x)аргументийн бүх утгын хувьд xтэгш бус байдлыг хангана f(x)≥ g(x)мөн хязгаартай бол тэгш бус байдал бий болно b≥c.

Баталгаа.Теоремын дагуу f(x)-g(x) ≥0Тиймээс 5-р теоремоор , эсвэл .

НЭГ ТАЛТЫН ХЯЗГААР

Одоогоор бид функцийн хязгаарын тодорхойлолтыг авч үзсэн x→aдур зоргоороо, i.e. Функцийн хязгаар нь хэрхэн хийхээс хамаарахгүй xчиглэсэн а, зүүн эсвэл баруун талд а. Гэсэн хэдий ч, энэ нөхцөлд хязгааргүй функцүүдийг олох нь нэлээд түгээмэл байдаг, гэхдээ тэдгээр нь хэрэв хязгаартай байдаг x→a, нэг талд байрлах а, зүүн эсвэл баруун (зураг харна уу). Тиймээс нэг талын хязгаарлалт гэсэн ойлголтыг оруулж ирж байна.

Хэрвээ f(x)хязгаар руу чиглэдэг бцагт xтодорхой тооны төлөө хичээж байна атийм x-аас бага утгыг л авдаг а, дараа нь бичээд залгана уу f(x) функцийн хязгаар зүүн талын а цэгт.

Хязгааргүй жижиг ба том тоонуудын тооцоо

Хязгааргүй жижиг тооцоо- үүсмэл үр дүнг хязгааргүй жижиг утгуудын хязгааргүй нийлбэр гэж үздэг хязгааргүй жижиг утгуудаар хийсэн тооцоолол. Хязгааргүй жижиг тооллын тооцоо нь орчин үеийн дээд математикийн үндэс болсон дифференциал ба интеграл тооцооллын ерөнхий ойлголт юм. Хязгааргүй хэмжигдэхүүний тухай ойлголт нь хязгаарын тухай ойлголттой нягт холбоотой.

Хязгааргүй жижиг

Дараалал а nдуудсан хязгааргүй жижиг, хэрэв . Жишээлбэл, тоонуудын дараалал нь хязгааргүй бага байдаг.

Функцийг дууддаг цэгийн ойролцоо хязгааргүй жижиг x 0 бол .

Функцийг дууддаг хязгааргүй жижиг, хэрэв эсвэл .

Мөн хязгааргүй жижиг функц нь функц ба түүний хязгаарын ялгаа, өөрөөр хэлбэл хэрэв , дараа нь е(x) − а = α( x) , .

хязгааргүй том

Доорх бүх томъёонд тэгш байдлын баруун талд байгаа хязгааргүй байдал нь тодорхой тэмдгийг ("нэмэх" эсвэл "хасах") илэрхийлдэг. Энэ нь жишээлбэл, функц юм xнүгэл x, хоёр талдаа хязгааргүй, -ийн хувьд хязгааргүй том биш.

Дараалал а nдуудсан хязгааргүй том, хэрэв .

Функцийг дууддаг цэгийн ойролцоо хязгааргүй том x 0 бол .

Функцийг дууддаг хязгааргүйд хязгааргүй том, хэрэв эсвэл .

Хязгааргүй ба хязгааргүй жижиг тоонуудын шинж чанарууд

Хязгааргүй жижиг тоонуудын харьцуулалт

Хязгааргүй жижиг хэмжигдэхүүнүүдийг хэрхэн харьцуулах вэ?
Хязгааргүй жижиг хэмжигдэхүүнүүдийн харьцаа нь тодорхойгүй байдлыг үүсгэдэг.

Тодорхойлолт

Ижил утгын хувьд бид хязгааргүй бага байна гэж бодъё α( x) ба β( x) (эсвэл тодорхойлолтод чухал биш, хязгааргүй жижиг дараалал).

Ийм хязгаарыг тооцоолохын тулд L'Hospital-ийн дүрмийг ашиглах нь тохиромжтой.

Харьцуулах жишээ

Ашиглаж байна О-гарсан үр дүнгийн тэмдэглэгээг дараах хэлбэрээр бичиж болно x 5 = о(x 3). Энэ тохиолдолд оруулгууд 2x 2 + 6x = О(x) болон x = О(2x 2 + 6x).

Тэнцүү хэмжигдэхүүнүүд

Тодорхойлолт

Хэрэв бол α ба β хязгааргүй жижиг хэмжигдэхүүнүүдийг дуудна тэнцүү ().
Мэдээжийн хэрэг, эквивалент хэмжигдэхүүн нь ижил жижиг дарааллын хязгааргүй жижиг хэмжигдэхүүнүүдийн онцгой тохиолдол юм.

-ийн хувьд дараах эквивалент харьцаа (гайхалтай хязгаар гэж нэрлэгддэг үр дагавар) байна.

Теорем

Хоёр хязгааргүй жижиг хэмжигдэхүүний (харьцаа) хязгаар нь тэдгээрийн аль нэгийг (эсвэл хоёуланг нь) эквивалент утгаар сольсон тохиолдолд өөрчлөгдөхгүй..

Энэ теорем нь хязгаарыг олоход практик ач холбогдолтой (жишээг үзнэ үү).

Хэрэглээний жишээ

Солих сбиn 2x эквивалент утга 2 x, бид авдаг

Түүхэн тойм

"Хязгааргүй жижиг" гэсэн ойлголтыг эрт дээр үед хуваагдашгүй атомын тухай ойлголттой холбон ярьж байсан ч сонгодог математикт орж ирээгүй. Дахин хэлэхэд энэ нь 16-р зуунд "хуваагдах арга" гарч ирснээр дахин сэргэсэн - судалж буй дүрсийг хязгааргүй жижиг хэсгүүдэд хуваах.

Хязгааргүй жижиг тооцооллын алгебрчлал 17-р зуунд болсон. Тэдгээрийг ямар ч төгсгөлтэй (тэг биш) утгаас бага боловч тэгтэй тэнцүү биш тоон утгууд гэж тодорхойлж эхэлсэн. Шинжилгээний урлаг нь хязгааргүй жижиг тоо (дифференциал) агуулсан харилцааг зохиож, дараа нь түүнийг нэгтгэх явдал байв.

Хуучин сургуулийн математикчид энэ үзэл баримтлалд хамрагдсан хязгааргүй жижигхатуу шүүмжлэл. Мишель Ролле шинэ тооцоо бол " гайхалтай алдаануудын багц»; Вольтер энэхүү тооцоолол нь оршин тогтнох нь нотлогдох боломжгүй зүйлсийг тооцоолох, нарийн хэмжих урлаг юм гэж хор хөнөөлтэй онцолсон. Гюйгенс хүртэл дээд эрэмбийн дифференциалын утгыг ойлгоогүй гэдгээ хүлээн зөвшөөрсөн.

Хувь заяаны инээдэм болгон зууны дунд үеийн стандарт бус шинжилгээний дүр төрхийг авч үзэх боломжтой бөгөөд энэ нь анхны үзэл бодол - бодит хязгаарлагдмал тоо баримт нь нийцэж байгааг нотолсон бөгөөд дүн шинжилгээ хийх үндэс болгон авч болно.

бас үзнэ үү

Викимедиа сан. 2010 он.

Бусад толь бичгүүдээс "Infinitesimal" гэж юу болохыг хараарай.

Хязгааргүй ЖИЖИГ- зарим процесс дахь хувьсагч, хэрэв энэ процесст энэ нь тэг рүү хязгааргүй ойртдог (тэмдэглэдэг) ... Их Политехник нэвтэрхий толь бичиг

хязгааргүй жижиг- ■ Үл мэдэгдэх зүйл боловч гомеопатитай холбоотой... Нийтлэг үнэний толь бичиг