ლექცია 4.

ფუნქციების უწყვეტობა

1. ფუნქციის უწყვეტობა წერტილში

განმარტება 1.დაუშვით ფუნქცია წ=ვ(x) განსაზღვრულია წერტილში X 0 და ამ წერტილის ზოგიერთ უბანში. ფუნქცია წ=ვ(x) ეწოდება უწყვეტი x წერტილში 0 , თუ ამ წერტილში არის ფუნქციის ზღვარი და ის უდრის ამ წერტილში ფუნქციის მნიშვნელობას, ე.ი.

ამგვარად, ფუნქციის უწყვეტობის პირობა წ=ვ(x) წერტილში X 0 არის ეს:

იმიტომ რომ
, მაშინ ტოლობა (32) შეიძლება დაიწეროს ფორმით

(33)

ეს ნიშნავს, რომ როცა უწყვეტი ფუნქციის ლიმიტის პოვნავ(x) შეიძლება ლიმიტამდე წასვლა ფუნქციის ნიშნის ქვეშ, ე.ი. ფუნქციაში ვ(x) არგუმენტის ნაცვლად Xშეცვალეთ მისი ზღვრული მნიშვნელობა X 0 .

lim sin x=ცოდვა (ლიმ x);

lim arctg x=arctg (ლიმ x); (34)

ლიმ ჟურნალი x=ლოგი (ლიმ x).

ვარჯიში.იპოვეთ ლიმიტი: 1)
; 2)
.

მოდით განვსაზღვროთ ფუნქციის უწყვეტობა არგუმენტისა და ფუნქციის გაზრდის ცნებებზე დაყრდნობით.

იმიტომ რომ პირობები
და
იდენტურია (ნახ. 4), შემდეგ ტოლობა (32) იღებს ფორმას:

ან
.

განმარტება 2.ფუნქცია წ=ვ(x) ეწოდება უწყვეტი x წერტილში 0 , თუ ის განსაზღვრულია წერტილში X 0 და მისი სამეზობლო, და უსასრულოდ მცირე ზრდა არგუმენტში შეესაბამება ფუნქციის უსასრულოდ მცირე ზრდას.

ვარჯიში.შეისწავლეთ ფუნქციის უწყვეტობა წ=2X 2 1.

ფუნქციების თვისებები უწყვეტი წერტილში

1. თუ ფუნქციები ვ(x) და φ (x) წერტილში უწყვეტია X 0, შემდეგ მათი ჯამი
, მუშაობა
და კერძო
(იმის გათვალისწინებით
) არის უწყვეტი ფუნქციები წერტილში X 0 .

2. თუ ფუნქცია ზე=ვ(x) წერტილში უწყვეტია X 0 და ვ(x 0)>0, მაშინ არის წერტილის ასეთი მეზობლობა X 0, რომელშიც ვ(x)>0.

3. თუ ფუნქცია ზე=ვ(u) უწყვეტია u 0 წერტილში და ფუნქცია u= φ (x) წერტილში უწყვეტია u 0 = φ (x 0 ), შემდეგ რთული ფუნქცია წ=ვ[φ (x)] არის უწყვეტი წერტილი X 0 .

2. ფუნქციის უწყვეტობა ინტერვალში და სეგმენტზე

ფუნქცია წ=ვ(x) ეწოდება უწყვეტი ინტერვალში (ა; ბ), თუ იგი უწყვეტია ამ ინტერვალის ყველა წერტილში.

ფუნქცია წ=ვ(x) ეწოდება უწყვეტი სეგმენტზე [ა; ბ] თუ ის უწყვეტია ინტერვალში ( ა; ბ), და იმ წერტილში X=ასწორია უწყვეტი (ე.ი.
), და იმ წერტილში x=ბრჩება უწყვეტი (ე.ი.
).

3. ფუნქციის შეწყვეტის წერტილები და მათი კლასიფიკაცია

 წერტილები, რომლებშიც ფუნქციის უწყვეტობა ირღვევა, ეწოდება შესვენების წერტილებიამ ფუნქციას.

თუ X=X 0 - ფუნქციის შესვენების წერტილი წ=ვ(x), მაშინ ფუნქციის უწყვეტობის პირველი განსაზღვრის ერთ-ერთი პირობა მაინც არ არის დაკმაყოფილებული.

მაგალითი.

1.
. 2.

3)
4)
.

▼ შესვენების წერტილი X 0-ს ეწოდება შესვენების წერტილი პირველი სახისფუნქციები წ=ვ(x), თუ ამ მომენტში არის ფუნქციის სასრული საზღვრები მარცხნივ და მარჯვნივ (ცალმხრივი საზღვრები), ე.ი.
და
. ამ შემთხვევაში:

მაგნიტუდა | ა 1 -ა 2 | დაურეკა ფუნქციური ნახტომიპირველი სახის შეწყვეტის წერტილში. ▲

▼ შესვენების წერტილი X 0-ს ეწოდება შესვენების წერტილი მეორე სახისფუნქციები წ=ვ(x), თუ ცალმხრივი ზღვრებიდან ერთი მაინც (მარცხნივ ან მარჯვნივ) არ არსებობს ან უდრის უსასრულობას. ▲

ვარჯიში.იპოვეთ შესვენების წერტილები და გაარკვიეთ მათი ტიპი ფუნქციებისთვის:

1)
; 2)
.

4. ძირითადი თეორემები უწყვეტი ფუნქციების შესახებ

ფუნქციების უწყვეტობის შესახებ თეორემები პირდაპირ გამომდინარეობს ლიმიტების შესახებ შესაბამისი თეორემებიდან.

თეორემა 1.ორი უწყვეტი ფუნქციის ჯამი, ნამრავლი და კოეფიციენტი არის უწყვეტი ფუნქცია (რაოდენობისთვის, გარდა არგუმენტის იმ მნიშვნელობებისა, რომლებშიც გამყოფი არ არის ნულის ტოლი).

თეორემა 2.დაუშვით ფუნქციები u=φ (x) წერტილში უწყვეტია X 0 და ფუნქცია წ=ვ(u) წერტილში უწყვეტია u=φ (x 0 ). შემდეგ კომპლექსური ფუნქცია ვ(φ (x)), რომელიც შედგება უწყვეტი ფუნქციებისგან, უწყვეტია წერტილში X 0 .

თეორემა 3.თუ ფუნქცია წ=ვ(x) არის უწყვეტი და მკაცრად ერთფეროვანი [ ა; ბ] ცულები ოჰ, შემდეგ შებრუნებული ფუნქცია ზე=φ (x) ასევე უწყვეტი და მონოტონურია შესაბამის სეგმენტზე [ გ;დ] ცულები ოჰ.

ნებისმიერი ელემენტარული ფუნქციაუწყვეტი ყველა წერტილში, სადაც ის განისაზღვრება.

5. ინტერვალზე უწყვეტი ფუნქციების თვისებები

ვაიერშტრასის თეორემა.თუ ფუნქცია უწყვეტია სეგმენტზე, მაშინ ის აღწევს მაქსიმალურ და მინიმალურ მნიშვნელობებს ამ სეგმენტზე.

შედეგი.თუ ფუნქცია უწყვეტია ინტერვალზე, მაშინ ის შემოსაზღვრულია ინტერვალზე.

ბოლცანო-კოშის თეორემა.თუ ფუნქცია წ=ვ(x) არის უწყვეტი ინტერვალზე [ ა; ბ] და იღებს არათანაბარ მნიშვნელობებს მის ბოლოებში ვ(ა)=ადა ვ(ბ)=ბ,
, მაშინ რაც არ უნდა იყოს ნომერი თანშორის დადებული ადა IN,არის წერტილი
ისეთი რომ ვ(გ)=C.

გეომეტრიულადთეორემა აშკარაა. ნებისმიერი ნომრისთვის თანშორის დადებული ადა IN, ამ სეგმენტის შიგნით არის c წერტილი ისეთი, რომ ვ(თან)=C. პირდაპირ ზე=თანკვეთს ფუნქციის გრაფიკს ერთ წერტილზე მაინც.

შედეგი.თუ ფუნქცია წ=ვ(x) არის უწყვეტი ინტერვალზე [ ა; ბ] და იღებს სხვადასხვა ნიშნის მნიშვნელობებს მის ბოლოებში, შემდეგ სეგმენტში [ ა; ბ] არის ერთი წერტილი მაინც თან, რომელშიც ფუნქცია წ=ვ(x) მიდის ნულზე: ვ(გ)=0.

გეომეტრიულითეორემის მნიშვნელობა: თუ უწყვეტი ფუნქციის გრაფიკი გადის ღერძის ერთი მხრიდან ოჰმეორეს, შემდეგ ის კვეთს ღერძს ოჰ.

ფუნქციის უწყვეტობა წერტილში

დაე, ფუნქცია f(x) განისაზღვროს x0 წერტილის O(x0) (თავად x0 წერტილის ჩათვლით) რომელიმე უბანში.

ფუნქცია f(x) ეწოდება უწყვეტს x0 წერტილში, თუ არსებობს limx → x0 f(x) ამ წერტილში f(x) ფუნქციის მნიშვნელობის ტოლი: lim

f(x) = f(x0), (1)

იმათ. "O(f(x0)) $ O(x0) : x O O(x0) Yu f(x) O O(f(x0)) .

კომენტარი. ტოლობა (1) შეიძლება დაიწეროს როგორც: lim

იმათ. უწყვეტი ფუნქციის ნიშნით შეიძლება ლიმიტამდე გადასვლა.

დავუშვათ Δx = x − x0 არგუმენტის ნამატი, Δy = f(x) − f(x0) ფუნქციის შესაბამისი ზრდა.

საჭირო და საკმარისი მდგომარეობაფუნქციის უწყვეტობა წერტილში

ფუნქცია y = f(x) უწყვეტია x0-ზე თუ და მხოლოდ მაშინ

კომენტარი. პირობა (2) შეიძლება განიმარტოს, როგორც ფუნქციის უწყვეტობის მეორე განმარტება წერტილში. ორივე განმარტება ექვივალენტურია.

დაე, ფუნქცია f(x) განისაზღვროს ნახევარინტერვალში.

ფუნქცია f(x) ითვლება უწყვეტად x0-ზე, თუ არსებობს ცალმხრივი ლიმიტი

ორი უწყვეტი ფუნქციის ჯამის, ნამრავლის და კოეფიციენტის უწყვეტობა

თეორემა 1. თუ f(x) და g(x) ფუნქციები უწყვეტია x0 წერტილში, მაშინ f(x) ± g(x), f(x) g(x), f(x) უწყვეტია აქ. წერტილი

რთული ფუნქციის უწყვეტობა

თეორემა 2. თუ ფუნქცია u(x) უწყვეტია x0 წერტილში, ხოლო f(u) ფუნქცია უწყვეტია შესაბამის წერტილში u0 = f(x0), მაშინ რთული ფუნქცია f(u(x)) უწყვეტია. x0 წერტილში.

ყველა ელემენტარული ფუნქცია უწყვეტია მათი განსაზღვრის სფეროს ყველა წერტილში.

უწყვეტი ფუნქციების ლოკალური თვისებები

თეორემა 3 (უწყვეტი ფუნქციის საზღვარი).

თუ ფუნქცია f(x) უწყვეტია x0-ზე, მაშინ არის O(x0) უბანი, რომელშიც f(x) არის შემოსაზღვრული.

მტკიცებულება გამომდინარეობს განცხადებაში ფუნქციის შეზღუდვის შესახებ, რომელსაც აქვს ლიმიტი.

თეორემა 4 (უწყვეტი ფუნქციის ნიშნის სტაბილურობა).

თუ ფუნქცია f(x) უწყვეტია x0 წერტილში და f(x0) ≠ 0, მაშინ არის x0 წერტილის სამეზობლო, რომელშიც f(x) ≠ 0 და f(x) ნიშანი ამ სამეზობლოში. ემთხვევა f(x0) ნიშანს.

შესვენების წერტილების კლასიფიკაცია

პირობა (1) f(x) ფუნქციის უწყვეტობისთვის x0 წერტილში არის პირობის ექვივალენტური f(x0 − 0) = f(x0 + 0) = f(x0), (3)

სადაც f(x 0 − 0) = lim

f(x) და f(x0 + 0) = lim

f(x) - f(x) ფუნქციის ცალმხრივი ზღვრები x0 წერტილში.

თუ (3) პირობა დარღვეულია, x0 წერტილს ეწოდება f(x) ფუნქციის უწყვეტობის წერტილი. (3) პირობის დარღვევის სახეობიდან გამომდინარე, შესვენების წერტილებს განსხვავებული ხასიათი აქვთ და კლასიფიცირდება შემდეგნაირად:

1. თუ x0 წერტილში არის ცალმხრივი ზღვრები f(x0 − 0), f (x0 + 0) და

f(x0 − 0) = f(x0 + 0) ≠ f(x0), მაშინ x0 წერტილს ეწოდება f(x) ფუნქციის მოხსნადი შეწყვეტის წერტილი (ნახ. 1).

კომენტარი. x0 წერტილში ფუნქცია შეიძლება არ იყოს განსაზღვრული.

2. თუ x0 წერტილში არის ცალმხრივი ზღვრები f(x0 − 0), f (x0 + 0) და

f(x0 − 0) ≠ f(x0 + 0), მაშინ x0 წერტილს ეწოდება უწყვეტობის წერტილი f(x) ფუნქციის სასრული ნახტომით (ნახ. 2). კომენტარი. შეწყვეტის წერტილში სასრული ნახტომით, ფუნქციის მნიშვნელობა შეიძლება იყოს ნებისმიერი, ან შეიძლება არ იყოს განსაზღვრული.მოხსნადი წყვეტისა და სასრული ნახტომის წერტილებს 1-ლი სახის შეწყვეტის წერტილებს უწოდებენ. მათი

3. თუ x0 წერტილში ცალმხრივი ზღვრებიდან ერთი მაინც f(x0 − 0), f (x0 + 0) უსასრულობის ტოლია ან არ არსებობს, მაშინ
x0 ეწოდება მე-2 ტიპის შეწყვეტის წერტილს (ნახ. 3).

თუ ცალმხრივი ზღვრებიდან ერთი მაინც f(x0 − 0), f (x0 + 0) უსასრულობის ტოლია, მაშინ სწორ ხაზს x = x 0 ეწოდება y = f ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტა. (x).

განმარტება. ფუნქცია f(x), რომელიც განსაზღვრულია x0 წერტილის სამეზობლოში, ეწოდება უწყვეტს x0 წერტილში, თუ ფუნქციის ზღვარი და მისი მნიშვნელობა ამ წერტილში ტოლია, ე.ი.

ერთი და იგივე ფაქტი შეიძლება სხვანაირად დაიწეროს:

განმარტება. თუ ფუნქცია f(x) განისაზღვრა x0 წერტილის რომელიმე სამეზობლოში, მაგრამ არ არის უწყვეტი თვით x0 წერტილში, მაშინ მას უწოდებენ წყვეტილ ფუნქციას, ხოლო x0 წერტილს - წყვეტის წერტილს.

განმარტება. ფუნქცია f(x) არის უწყვეტი x0 წერტილში, თუ ასეთია დადებითი რიცხვი e>0 არის რიცხვი D>0 ისეთი, რომ ნებისმიერი x-ისთვის, რომელიც აკმაყოფილებს პირობას

უთანასწორობა მართალია.

განმარტება.

ფუნქცია f(x) ეწოდება უწყვეტს x = x0 წერტილში, თუ ფუნქციის ზრდა x0 წერტილში არის უსასრულოდ მცირე მნიშვნელობა.

f(x) = f(x0) + a(x)

სადაც a(x) არის უსასრულოდ მცირე x®x0-ზე.

უწყვეტი ფუნქციების თვისებები.

1) x0 წერტილში უწყვეტი ფუნქციების ჯამი, სხვაობა და ნამრავლი არის x0 წერტილში უწყვეტი ფუნქცია. 2) ორი უწყვეტი ფუნქციის კოეფიციენტიაუწყვეტი ფუნქცია

იმ პირობით, რომ g(x) x0 წერტილში ნულის ტოლი არ არის.

3) უწყვეტი ფუნქციების სუპერპოზიცია არის უწყვეტი ფუნქცია.

ეს ქონება შეიძლება ჩაიწეროს შემდეგნაირად:

თუ u = f(x), v = g(x) არის უწყვეტი ფუნქციები x = x0 წერტილში, მაშინ ფუნქცია v = g(f(x)) ასევე უწყვეტი ფუნქციაა ამ წერტილში.

ზემოაღნიშნული თვისებების მართებულობა მარტივად შეიძლება დადასტურდეს ლიმიტის თეორემების გამოყენებით

ფუნქციების თვისებები უწყვეტი ინტერვალზე.

თვისება 1: (ვაიერშტრასის პირველი თეორემა (ვაიერშტრას კარლ (1815-1897) - გერმანელი მათემატიკოსი)). ფუნქცია, რომელიც უწყვეტია ინტერვალზე, შემოიფარგლება ამ ინტერვალზე, ე.ი. პირობა –M £ f(x) £ M დაკმაყოფილებულია სეგმენტზე.

ამ თვისების მტკიცებულება ემყარება იმ ფაქტს, რომ ფუნქცია, რომელიც არის უწყვეტი x0 წერტილში, შემოიფარგლება მის გარკვეულ სამეზობლოში, და თუ სეგმენტს დაყოფთ უსასრულო რაოდენობის სეგმენტებად, რომლებიც „შეკუმშულია“ x0 წერტილამდე. , მაშინ იქმნება x0 წერტილის გარკვეული მეზობლობა.

თვისება 2: სეგმენტზე უწყვეტი ფუნქცია იღებს მასზე უდიდეს და უმცირეს მნიშვნელობებს.

იმათ. არსებობს მნიშვნელობები x1 და x2 ისეთი, რომ f(x1) = m, f(x2) = M და

განსხვავებას ფუნქციის უდიდეს და უმცირეს მნიშვნელობას შორის ინტერვალზე ეწოდება ფუნქციის რხევა ინტერვალზე.

თვისება 3: (მეორე ბოლზანო-კოშის თეორემა). ფუნქცია, რომელიც უწყვეტია ინტერვალზე, იღებს ყველა მნიშვნელობას ამ ინტერვალზე ორ თვითნებურ მნიშვნელობას შორის.

თვისება 4: თუ ფუნქცია f(x) უწყვეტია x = x0 წერტილში, მაშინ არის x0 წერტილის რაღაც სამეზობლო, რომელშიც ფუნქცია ინარჩუნებს თავის ნიშანს.

თვისება 5: (ბოლცანოს პირველი თეორემა (1781-1848) – კოში). თუ ფუნქცია f(x) უწყვეტია სეგმენტზე და აქვს საპირისპირო ნიშნების მნიშვნელობები სეგმენტის ბოლოებში, მაშინ ამ სეგმენტის შიგნით არის წერტილი, სადაც f(x) = 0.

იმათ. თუ ნიშანი(f(a)) ¹ ნიშანი(f(b)), მაშინ $ x0: f(x0) = 0.

განმარტება. ფუნქცია f(x) ითვლება ერთნაირად უწყვეტი ინტერვალზე, თუ ნებისმიერი e>0-სთვის არსებობს D>0 ისეთი, რომ ნებისმიერი წერტილისთვის x1О და x2О ისეთი, რომ

ïx2 – x1ï< D

უტოლობა ïf(x2) – f(x1)ï მართალია< e

განსხვავება ერთგვაროვან უწყვეტობასა და „ჩვეულებრივ“ უწყვეტობას შორის არის ის, რომ ნებისმიერი e-სთვის არის საკუთარი D, x-ისგან დამოუკიდებელი, ხოლო „ჩვეულებრივი“ უწყვეტობით D დამოკიდებულია e-ზე და x-ზე.

თვისება 6: კანტორის თეორემა (გეორგ კანტორი (1845-1918) - გერმანელი მათემატიკოსი). სეგმენტზე უწყვეტი ფუნქცია მასზე ერთნაირად უწყვეტია.

(ეს თვისება მართალია მხოლოდ სეგმენტებისთვის და არა ინტერვალებისთვის და ნახევრად ინტერვალებისთვის.)

უწყვეტობის განმარტება

ფუნქცია f (x) ეწოდება უწყვეტს a წერტილში, თუ: f () pp

1) ფუნქცია f(x) განისაზღვრება a წერტილში,

2) აქვს სასრული ზღვარი, როგორც x→ a 2) აქვს სასრული ზღვარი, როგორც x→ a,

3) ეს ზღვარი უდრის ფუნქციის მნიშვნელობას ამ ეტაპზე:

უწყვეტობა ინტერვალში

ფუნქცია f (x) ითვლება უწყვეტად X ინტერვალზე, თუ f () pp ru

ის უწყვეტია ამ ინტერვალის ყველა წერტილში.

განცხადება. ყველა ელემენტარული ფუნქცია უწყვეტია

მათი განმარტების სფეროები.

შემოსაზღვრული ფუნქცია

ამბობენ, რომ ფუნქცია შეზღუდულია თუ ინტერვალზე

არის რიცხვი M ისეთი, რომ ყველა x ∈

უთანასწორობა:| f(x)| ≤ მ.

ვაიერშტრასის ორი თეორემა

ვაიერშტრასის პირველი თეორემა. თუ ფუნქცია f (x r r r r f f (

უწყვეტია სეგმენტზე, შემდეგ ის შემოიფარგლება ამ სეგმენტზე

ვაიერშტრასის მეორე თეორემა.თუ ფუნქცია f(x

არის უწყვეტი სეგმენტზე, შემდეგ ის აღწევს ამ სეგმენტს

m-ის უმცირესი მნიშვნელობა და M-ის უდიდესი მნიშვნელობა.

ბოლცანო-კოშის თეორემა

თუ ფუნქცია f (x) უწყვეტია მნიშვნელობის სეგმენტზე f f () pp p

ამ სეგმენტის ბოლოებზე f(a) და f(b) აქვთ საპირისპირო ნიშნები,

სეგმენტის შიგნით არის წერტილი c∈ (a,b) ისეთი, რომ f (c) = 0. ur p () f ()

ფუნქციის უწყვეტობა. დარღვევის წერტილები.

ხარი დადის, ქანაობს, კვნესის, როცა მიდის:
- ოჰ, დაფა იწურება, ახლა ვაპირებ ჩავარდნას!

ამ გაკვეთილზე განვიხილავთ ფუნქციის უწყვეტობის ცნებას, წყვეტის წერტილების კლასიფიკაციას და საერთო პრაქტიკული პრობლემა ფუნქციების უწყვეტობის შესწავლა. თემის სახელიდან ბევრი ინტუიციურად გამოიცნობს რაზე იქნება საუბარი და ფიქრობს, რომ მასალა საკმაოდ მარტივია. ეს მართალია. მაგრამ ეს არის მარტივი ამოცანები, რომლებიც ყველაზე ხშირად ისჯება უგულებელყოფისა და მათი გადაჭრის ზედაპირული მიდგომისთვის. ამიტომ, გირჩევთ, რომ ძალიან ფრთხილად შეისწავლოთ სტატია და დაიჭიროთ ყველა დახვეწილობა და ტექნიკა.

რა უნდა იცოდე და შეგეძლოს?არა ძალიან. იმისათვის, რომ კარგად ისწავლოთ გაკვეთილი, უნდა გესმოდეთ, რა არის ეს ფუნქციის ლიმიტი . მომზადების დაბალი დონის მკითხველისთვის საკმარისია სტატიის გააზრება ფუნქციის შეზღუდვები. გადაწყვეტილებების მაგალითები და ნახე გეომეტრიული მნიშვნელობალიმიტი სახელმძღვანელოში ელემენტარული ფუნქციების გრაფიკები და თვისებები . ასევე სასურველია გაეცნოთ გრაფიკების გეომეტრიული გარდაქმნები , ვინაიდან პრაქტიკა უმეტეს შემთხვევაში გულისხმობს ნახატის აგებას. პერსპექტივები ყველასთვის ოპტიმისტურია და სავსე ქვაბიც კი შეძლებს დამოუკიდებლად გაუმკლავდეს დავალებას მომდევნო საათში ან ორ საათში!

ფუნქციის უწყვეტობა. წყვეტების წერტილები და მათი კლასიფიკაცია

ფუნქციის უწყვეტობის კონცეფცია

განვიხილოთ რამდენიმე ფუნქცია, რომელიც უწყვეტია მთელ რიცხვით წრფეზე:

ან, უფრო მოკლედ რომ ვთქვათ, ჩვენი ფუნქცია უწყვეტია (ნამდვილი რიცხვების სიმრავლე).

რა არის უწყვეტობის „ფილისტური“ კრიტერიუმი? ცხადია, უწყვეტი ფუნქციის გრაფიკის დახატვა შესაძლებელია ფურცლიდან ფანქრის აწევის გარეშე.

ამ შემთხვევაში ნათლად უნდა გამოიყოს ორი მარტივი ცნება: ფუნქციის დომენი და ფუნქციის უწყვეტობა. ზოგადად ეს არ არის იგივე. მაგალითად:

ეს ფუნქციაგანსაზღვრულია მთელ რიცხვთა წრფეზე, ანუ for ყველას"x"-ის მნიშვნელობას აქვს "y"-ის საკუთარი მნიშვნელობა. კერძოდ, თუ, მაშინ. გაითვალისწინეთ, რომ სხვა წერტილი პუნქტუირებულია, რადგან ფუნქციის განმარტებით, არგუმენტის მნიშვნელობა უნდა შეესაბამებოდეს ერთადერთი რამფუნქციის მნიშვნელობა. ამრიგად, განმარტების სფერო ჩვენი ფუნქცია:.

თუმცა ეს ფუნქცია არ არის უწყვეტი ჩართული!აშკარაა, რომ ამ ეტაპზე ის იტანჯება უფსკრული. ტერმინი ასევე საკმაოდ გასაგები და ვიზუალურია, აქ ფანქარი მაინც უნდა მოიგლიჯოს. ცოტა მოგვიანებით განვიხილავთ წყვეტის წერტილების კლასიფიკაციას.

ფუნქციის უწყვეტობა წერტილში და ინტერვალზე

ასეა თუ ისე მათემატიკის პრობლემაჩვენ შეგვიძლია ვისაუბროთ ფუნქციის უწყვეტობაზე წერტილში, ფუნქციის უწყვეტობაზე ინტერვალზე, ნახევარინტერვალზე ან ფუნქციის უწყვეტობაზე სეგმენტზე. ანუ არ არსებობს "უბრალო უწყვეტობა"– ფუნქცია შეიძლება იყოს უწყვეტი სადღაც. და ყველაფრის ფუნდამენტური "სამშენებლო ბლოკი" არის ფუნქციის უწყვეტობა წერტილში .

თეორია მათემატიკური ანალიზიიძლევა ფუნქციის უწყვეტობის განმარტებას წერტილში „დელტას“ და „ეპსილონის“ უბნების გამოყენებით, მაგრამ პრაქტიკაში სხვა განმარტება გამოიყენება, რომელსაც ჩვენ დიდ ყურადღებას მივაქცევთ.

ჯერ გავიხსენოთ ცალმხრივი საზღვრებივინც პირველ გაკვეთილზე შემოიჭრა ჩვენს ცხოვრებაში ფუნქციების გრაფიკების შესახებ . განვიხილოთ ყოველდღიური სიტუაცია:

თუ ღერძს მივუახლოვდებით წერტილს დატოვა(წითელი ისარი), შემდეგ "თამაშების" შესაბამისი მნიშვნელობები მიდის ღერძის გასწვრივ წერტილამდე (ჟოლოსფერი ისარი). მათემატიკურად, ეს ფაქტი ფიქსირდება გამოყენებით მარცხენა ლიმიტი:

ყურადღება მიაქციეთ ჩანაწერს (წაკითხულია "x tends to ka მარცხნივ"). "დანამატი" "მინუს ნული" სიმბოლოა , არსებითად ეს ნიშნავს, რომ ჩვენ ვუახლოვდებით რიცხვს მარცხენა მხრიდან.

ანალოგიურად, თუ მიუახლოვდებით წერტილს "ka" უფლება(ლურჯი ისარი), შემდეგ "თამაშები" მივა იგივე მნიშვნელობამდე, მაგრამ მწვანე ისრის გასწვრივ და მარჯვენა ლიმიტიფორმატირებული იქნება შემდეგნაირად:

„დანამატი“ სიმბოლოა , და ჩანაწერში ნათქვამია: „x მიდრეკილია ka-სკენ მარჯვნივ“.

თუ ცალმხრივი ზღვრები სასრული და ტოლია(როგორც ჩვენს შემთხვევაში): , მაშინ ვიტყვით, რომ არსებობს ზოგადი ლიმიტი. ეს მარტივია, ზოგადი ზღვარი არის ჩვენი "ჩვეულებრივი" ფუნქციის ლიმიტი , უდრის სასრულ რიცხვს.

გაითვალისწინეთ, რომ თუ ფუნქცია არ არის განსაზღვრული (გამოიღეთ შავი წერტილი გრაფიკის ტოტზე), მაშინ ზემოაღნიშნული გამოთვლები ძალაში რჩება. როგორც უკვე არაერთხელ აღინიშნა, კერძოდ სტატიაში უსასრულოდ მცირე ფუნქციებზე , გამონათქვამები ნიშნავს, რომ "x" უსასრულოდ ახლოსუახლოვდება წერტილს, ხოლო არ აქვს მნიშვნელობა, განსაზღვრულია თუ არა თავად ფუნქცია მოცემულ წერტილში. კარგი მაგალითიგამოჩნდება შემდეგ აბზაცში, როდესაც მოხდება ფუნქციის ანალიზი.

განმარტება: ფუნქცია უწყვეტია წერტილში, თუ ფუნქციის ზღვარი მოცემულ წერტილში უდრის ფუნქციის მნიშვნელობას ამ წერტილში: .

განმარტება დეტალურად არის აღწერილი შემდეგ ტერმინებში:

1) ფუნქცია უნდა განისაზღვროს წერტილში, ანუ მნიშვნელობა უნდა არსებობდეს.

2) უნდა არსებობდეს ფუნქციის ზოგადი ლიმიტი. როგორც ზემოთ აღინიშნა, ეს გულისხმობს ცალმხრივი საზღვრების არსებობას და თანასწორობას: .

3) მოცემულ წერტილში ფუნქციის ზღვარი უნდა იყოს ამ წერტილის ფუნქციის მნიშვნელობის ტოლი: .

თუ დაირღვა ერთი მაინცსამი პირობის, მაშინ ფუნქცია კარგავს უწყვეტობის თვისებას წერტილში.

ფუნქციის უწყვეტობა ინტერვალზეფორმულირებულია გენიალურად და ძალიან მარტივად: ფუნქცია უწყვეტია ინტერვალზე, თუ ის უწყვეტია მოცემული ინტერვალის ყველა წერტილში.

კერძოდ, ბევრი ფუნქცია უწყვეტია უსასრულო ინტერვალზე, ანუ რეალური რიცხვების სიმრავლეზე. ეს არის წრფივი ფუნქცია, პოლინომები, ექსპონენციალური, სინუსი, კოსინუსი და ა.შ. და ზოგადად, ნებისმიერი ელემენტარული ფუნქცია უწყვეტი მასზე განმარტების სფერო მაგალითად, ლოგარითმული ფუნქცია უწყვეტია ინტერვალზე. იმედი მაქვს ამ მომენტშითქვენ გაქვთ საკმაოდ კარგი წარმოდგენა იმის შესახებ, თუ როგორ გამოიყურება ძირითადი ფუნქციების გრაფიკები. მეტი დეტალური ინფორმაციამათი უწყვეტობის გარკვევა შესაძლებელია კეთილი ადამიანიგვარად ფიხტენგოლცი.

სეგმენტზე ფუნქციის უწყვეტობით და ნახევრად ინტერვალებით, ყველაფერი ასევე არ არის რთული, მაგრამ ამაზე საუბარი უფრო მიზანშეწონილია კლასში სეგმენტზე ფუნქციის მინიმალური და მაქსიმალური მნიშვნელობების პოვნის შესახებ , მაგრამ ახლა ამაზე არ ინერვიულოთ.

შესვენების წერტილების კლასიფიკაცია

ფუნქციების მომხიბლავი ცხოვრება მდიდარია ყველა სახის განსაკუთრებული პუნქტით და შესვენების წერტილები მათი ბიოგრაფიის მხოლოდ ერთ-ერთი გვერდია.

შენიშვნა : ყოველი შემთხვევისთვის, ელემენტარულ პუნქტზე შევჩერდები: წყვეტის წერტილი ყოველთვის არის ერთი წერტილი– არ არსებობს „რამდენიმე შესვენების წერტილი ზედიზედ“, ანუ არ არსებობს „შესვენების ინტერვალი“.

ეს პუნქტები, თავის მხრივ, იყოფა ორ დიდ ჯგუფად: პირველი სახის რღვევებიდა მეორე სახის რღვევები. თითოეული ტიპის უფსკრული აქვს საკუთარი დამახასიათებელი ნიშნებირომელსაც ახლავე განვიხილავთ:

პირველი ტიპის შეწყვეტის წერტილი

თუ უწყვეტობის პირობა ირღვევა წერტილში და ცალმხრივი საზღვრები სასრული , მაშინ ე.წ პირველი ტიპის შეწყვეტის წერტილი.

დავიწყოთ ყველაზე ოპტიმისტური შემთხვევით. გაკვეთილის თავდაპირველი იდეის მიხედვით, მინდოდა მეთქვა თეორია „ში ზოგადი ხედი”, მაგრამ მასალის რეალობის დემონსტრირების მიზნით, მე გადავწყვიტე ვარიანტი კონკრეტული სიმბოლოებით.

სამწუხაროა, როგორც ახალდაქორწინებულთა ფოტო მარადიული ცეცხლის ფონზე, მაგრამ შემდეგი კადრი ზოგადად მიღებულია. მოდით გამოვსახოთ ნახაზზე ფუნქციის გრაფიკი:


ეს ფუნქცია უწყვეტია მთელ რიცხვით წრფეზე, წერტილის გარდა. და ფაქტობრივად, მნიშვნელი არ შეიძლება იყოს ნულის ტოლი. თუმცა, ლიმიტის მნიშვნელობის შესაბამისად, შეგვიძლია უსასრულოდ ახლოსმიუახლოვდით "ნულს" როგორც მარცხნიდან, ასევე მარჯვნიდან, ანუ ცალმხრივი საზღვრები არსებობს და, ცხადია, ემთხვევა:
(უწყვეტობის No2 პირობა დაკმაყოფილებულია).

მაგრამ ფუნქცია არ არის განსაზღვრული წერტილში, შესაბამისად, დარღვეულია უწყვეტობის No1 პირობა და ფუნქცია ამ ეტაპზე განიცდის წყვეტას.

ამ ტიპის შესვენება (არსებულთან ზოგადი ლიმიტი) ეძახიან შესაკეთებელი უფსკრული. რატომ მოსახსნელი? რადგან ფუნქციას შეუძლია ხელახლა განსაზღვრაგატეხვის წერტილში:

უცნაურად გამოიყურება? შესაძლოა. მაგრამ ასეთი ფუნქციის აღნიშვნა არაფერს ეწინააღმდეგება! ახლა უფსკრული დაიხურა და ყველა ბედნიერია:


მოდით შევასრულოთ ოფიციალური შემოწმება:

2) - არსებობს ზოგადი ლიმიტი;
3)

ამრიგად, სამივე პირობა დაკმაყოფილებულია და ფუნქცია არის უწყვეტი წერტილში ფუნქციის უწყვეტობის განსაზღვრით.

თუმცა, მატანის მოძულეებს შეუძლიათ, მაგალითად, ფუნქცია ცუდად განსაზღვრონ :


საინტერესოა, რომ პირველი ორი უწყვეტობის პირობა დაკმაყოფილებულია აქ:
1) – ფუნქცია განსაზღვრულია მოცემულ წერტილში;
2) - არსებობს ზოგადი ზღვარი.

მაგრამ მესამე საზღვარი არ არის გავლილი: , ანუ ფუნქციის ზღვარი წერტილში არა თანაბარიმოცემული ფუნქციის მნიშვნელობა მოცემულ წერტილში.

ამრიგად, ერთ მომენტში ფუნქცია განიცდის შეწყვეტას.

მეორე, უფრო სევდიანი შემთხვევა ჰქვია პირველი სახის რღვევა ნახტომით. და სევდა გამოწვეულია ცალმხრივი საზღვრებით სასრული და განსხვავებული. მაგალითი ნაჩვენებია გაკვეთილის მეორე ნახატში. ასეთი უფსკრული ჩვეულებრივ ხდება ნაწილებად განსაზღვრული ფუნქციები, რომლებიც უკვე აღინიშნა სტატიაში გრაფიკის გარდაქმნების შესახებ .

განვიხილოთ ცალმხრივი ფუნქცია და ჩვენ დავასრულებთ მის ნახატს. როგორ ავაშენოთ გრაფიკი? ძალიან მარტივი. ნახევარი ინტერვალით ვხატავთ პარაბოლას ფრაგმენტს ( მწვანე), ინტერვალზე – სწორი ხაზის სეგმენტი (წითელი) და ნახევარინტერვალზე – სწორი ხაზი (ლურჯი).

უფრო მეტიც, უტოლობის გამო, მნიშვნელობა განისაზღვრება კვადრატული ფუნქციისთვის (მწვანე წერტილი), ხოლო უტოლობის გამო, მნიშვნელობა განისაზღვრება წრფივი ფუნქციისთვის (ლურჯი წერტილი):

ყველაზე რთულ შემთხვევაში, თქვენ უნდა მიმართოთ გრაფიკის თითოეული ნაწილის პუნქტ-პუნქტის აგებას (იხ. პირველი გაკვეთილი ფუნქციების გრაფიკების შესახებ ).

ახლა ჩვენ მხოლოდ საკითხი გვაინტერესებს. მოდით შევამოწმოთ იგი უწყვეტობისთვის:

2) გამოვთვალოთ ცალმხრივი ლიმიტები.

მარცხნივ გვაქვს წითელი ხაზის სეგმენტი, ამიტომ მარცხნივ ზღვარი არის:

მარჯვნივ არის ლურჯი სწორი ხაზი და მარჯვენა ზღვარი:

შედეგად მივიღეთ სასრული რიცხვებიდა ისინი არა თანაბარი. ვინაიდან ცალმხრივი ლიმიტები სასრული და განსხვავებული: , მაშინ ჩვენი ფუნქცია მოითმენს პირველი სახის შეწყვეტა ნახტომით.

ლოგიკურია, რომ ხარვეზის აღმოფხვრა შეუძლებელია - ფუნქციის შემდგომი განსაზღვრა და "ერთად დამაგრება" ნამდვილად შეუძლებელია, როგორც წინა მაგალითში.

მეორე სახის შეწყვეტის წერტილები

ჩვეულებრივ, რღვევის ყველა სხვა შემთხვევა ჭკვიანურად კლასიფიცირდება ამ კატეგორიაში. ყველაფერს არ ჩამოვთვლი, რადგან პრაქტიკაში პრობლემების 99%-ში შეგხვდებათ გაუთავებელი უფსკრული– როცა მემარცხენეა ან მემარჯვენე და უფრო ხშირად, ორივე ზღვარი უსასრულოა.

და, რა თქმა უნდა, ყველაზე თვალსაჩინო სურათი არის ჰიპერბოლა ნულოვან წერტილში. აქ ორივე ცალმხრივი ზღვარი უსასრულოა: მაშასადამე, ფუნქცია განიცდის მეორე სახის შეწყვეტას წერტილში.

ვცდილობ ჩემი სტატიები შევავსო რაც შეიძლება მრავალფეროვანი შინაარსით, ასე რომ, მოდით გადავხედოთ ფუნქციის გრაფიკს, რომელიც ჯერ არ შემხვედრია:

სტანდარტული სქემის მიხედვით:

1) ფუნქცია არ არის განსაზღვრული ამ ეტაპზე, რადგან მნიშვნელი მიდის ნულზე.

რა თქმა უნდა, დაუყოვნებლივ შეგვიძლია დავასკვნათ, რომ ფუნქცია განიცდის წყვეტას წერტილში, მაგრამ კარგი იქნება, რომ კლასიფიცირდეს შეწყვეტის ბუნება, რაც ხშირად მოითხოვს მდგომარეობას. ამის გასაკეთებლად:

შეგახსენებთ, რომ ჩაწერაში ვგულისხმობთ უსასრულო უარყოფითი რიცხვიდა ჩანაწერის ქვეშ - უსასრულოდ მცირე დადებითი რიცხვი.

ცალმხრივი საზღვრები უსასრულოა, რაც ნიშნავს, რომ ფუნქცია განიცდის მე-2 ტიპის შეწყვეტას წერტილში. y-ღერძი არის ვერტიკალური ასიმპტოტი გრაფიკისთვის.

არც ისე იშვიათია ორივე ცალმხრივი საზღვრების არსებობა, მაგრამ მხოლოდ ერთი მათგანია უსასრულო, მაგალითად:

ეს არის ფუნქციის გრაფიკი.

ჩვენ განვიხილავთ პუნქტს უწყვეტობისთვის:

1) ფუნქცია ამ ეტაპზე არ არის განსაზღვრული.

2) გამოვთვალოთ ცალმხრივი ლიმიტები: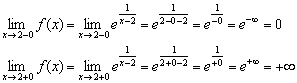

ასეთი ცალმხრივი ლიმიტების გამოთვლის მეთოდზე ვისაუბრებთ ლექციის ბოლო ორ მაგალითში, თუმცა ბევრმა მკითხველმა უკვე ყველაფერი ნახა და გამოიცნო.

მარცხენა ზღვარი არის სასრული და ნულის ტოლი (ჩვენ არ „მივდივართ“ თვით წერტილზე), მაგრამ მარჯვენა ზღვარი უსასრულოა და გრაფიკის ნარინჯისფერი ტოტი უსასრულოდ უახლოვდება მას. ვერტიკალური ასიმპტოტი , მოცემული განტოლებით (შავ წერტილოვანი ხაზი).

ასე რომ, ფუნქცია ზარალდება მეორე სახის შეწყვეტაწერტილში.

რაც შეეხება 1-ლი ტიპის წყვეტას, ფუნქცია შეიძლება განისაზღვროს თავად შეწყვეტის წერტილში. მაგალითად, ცალი ფუნქციისთვის თავისუფლად დააყენეთ შავი სქელი წერტილი კოორდინატების სათავეში. მარჯვნივ არის ჰიპერბოლის ტოტი, ხოლო მარჯვენა ზღვარი უსასრულოა. ვფიქრობ, თითქმის ყველას აქვს წარმოდგენა იმის შესახებ, თუ როგორ გამოიყურება ეს გრაფიკი.

რასაც ყველა მოუთმენლად ელოდა:

როგორ გამოვიკვლიოთ ფუნქცია უწყვეტობისთვის?

უწყვეტობის ფუნქციის შესწავლა წერტილში ხორციელდება უკვე დადგენილი რუტინული სქემის მიხედვით, რომელიც შედგება უწყვეტობის სამი პირობის შემოწმებისგან:

მაგალითი 1

შეისწავლეთ ფუნქცია

გამოსავალი:

1) მოქმედების ფარგლებში ერთადერთი წერტილია, სადაც ფუნქცია არ არის განსაზღვრული.

2) გამოვთვალოთ ცალმხრივი ლიმიტები:

ცალმხრივი საზღვრები სასრული და თანაბარია.

ამრიგად, იმ მომენტში ფუნქცია განიცდის მოსახსნელ შეწყვეტას.

როგორ გამოიყურება ამ ფუნქციის გრაფიკი?

გამარტივება მინდა და, როგორც ჩანს, ჩვეულებრივი პარაბოლა არის მიღებული. მაგრამთავდაპირველი ფუნქცია არ არის განსაზღვრული წერტილში, ამიტომ საჭიროა შემდეგი პუნქტი:

მოდით გავაკეთოთ ნახატი:

უპასუხე: ფუნქცია უწყვეტია მთელ რიცხვით წრფეზე, გარდა იმ წერტილისა, სადაც ის განიცდის მოსახსნელ წყვეტას.

ფუნქცია შეიძლება შემდგომ განისაზღვროს კარგი ან არც ისე კარგი გზით, მაგრამ პირობის მიხედვით ეს არ არის საჭირო.

თქვენ ამბობთ, რომ ეს შორეული მაგალითია? სულაც არა. პრაქტიკაში ეს ათეულჯერ მოხდა. საიტის თითქმის ყველა დავალება მოდის რეალური დამოუკიდებელი სამუშაოდან და ტესტებიდან.

მოვიშოროთ ჩვენი საყვარელი მოდულები:

მაგალითი 2

შეისწავლეთ ფუნქცია უწყვეტობისთვის. განსაზღვრეთ ფუნქციის უწყვეტობის ბუნება, თუ ისინი არსებობს. შეასრულეთ ნახაზი.

გამოსავალი: რატომღაც სტუდენტებს ეშინიათ და არ მოსწონთ ფუნქციები მოდულით, თუმცა მათში არაფერია რთული. ასეთ რამეებს გაკვეთილზე უკვე ცოტა შევეხეთ. გრაფიკების გეომეტრიული გარდაქმნები . ვინაიდან მოდული არანეგატიურია, ის გაფართოვდა შემდეგნაირად: , სადაც "ალფა" არის რაღაც გამოთქმა. IN ამ შემთხვევაშიდა ჩვენი ფუნქცია უნდა დაიწეროს ნაწილებად:

მაგრამ ორივე ნაწილის წილადები უნდა შემცირდეს . შემცირება, როგორც წინა მაგალითში, არ მოხდება შედეგების გარეშე. თავდაპირველი ფუნქცია არ არის განსაზღვრული წერტილში, რადგან მნიშვნელი მიდის ნულზე. ამიტომ სისტემამ დამატებით უნდა მიუთითოს პირობა და პირველი უტოლობა მკაცრი გახადოს:

ახლა ძალიან სასარგებლო გადაწყვეტილების ტექნიკის შესახებ: პროექტზე დავალების დასრულებამდე მიზანშეწონილია ნახაზის გაკეთება (მიუხედავად იმისა, ამას მოითხოვს პირობები თუ არა). ეს დაგეხმარებათ, პირველ რიგში, დაუყოვნებლივ დაინახოთ უწყვეტობის წერტილები და შეწყვეტის წერტილები, და მეორეც, ის 100%-ით დაგიცავთ შეცდომებისგან ცალმხრივი საზღვრების პოვნისას.

მოდით გავაკეთოთ ნახატი. ჩვენი გამოთვლების მიხედვით, წერტილიდან მარცხნივ აუცილებელია პარაბოლის ფრაგმენტის დახატვა (ლურჯი ფერი), ხოლო მარჯვნივ - პარაბოლის ცალი (წითელი ფერი), ხოლო ფუნქცია არ არის განსაზღვრული თავად მიუთითეთ:

თუ ეჭვი გაქვთ, აიღეთ რამდენიმე x მნიშვნელობა და შეაერთეთ ისინი ფუნქციაში (გახსოვდეთ, რომ მოდული ანადგურებს შესაძლო მინუს ნიშანს) და შეამოწმეთ გრაფიკი.

მოდით განვიხილოთ ფუნქცია უწყვეტობისთვის ანალიტიკურად:

1) ფუნქცია არ არის განსაზღვრული წერტილში, ამიტომ დაუყოვნებლივ შეგვიძლია ვთქვათ, რომ ის არ არის უწყვეტი მასში.

2) დავადგინოთ შეწყვეტის ბუნება, რომ გავაკეთოთ, გამოვთვალოთ ცალმხრივი ლიმიტები:

ცალმხრივი საზღვრები სასრული და განსხვავებულია, რაც ნიშნავს, რომ ფუნქცია განიცდის 1-ლი სახის შეწყვეტას წერტილში ნახტომით. კიდევ ერთხელ გაითვალისწინეთ, რომ ლიმიტების პოვნისას არ აქვს მნიშვნელობა განსაზღვრულია თუ არა ფუნქცია შესვენების წერტილში.

ახლა რჩება მხოლოდ ნახატის გადატანა მონახაზიდან (ის გაკეთდა თითქოს კვლევის დახმარებით ;-)) და დაასრულეთ დავალება:

უპასუხე: ფუნქცია უწყვეტია მთელ რიცხვით წრფეზე, გარდა იმ წერტილისა, სადაც ის განიცდის პირველი სახის წყვეტას ნახტომით.

ზოგჯერ ისინი საჭიროებენ უწყვეტი ნახტომის დამატებით მითითებას. იგი გამოითვლება უბრალოდ - მარჯვენა ზღვრიდან უნდა გამოკლოთ მარცხენა ლიმიტი: , ანუ შესვენების დროს ჩვენი ფუნქცია 2 ერთეულით ქვემოთ გადახტა (როგორც მინუს ნიშანი გვეუბნება).

მაგალითი 3

შეისწავლეთ ფუნქცია უწყვეტობისთვის. განსაზღვრეთ ფუნქციის უწყვეტობის ბუნება, თუ ისინი არსებობს. გააკეთე ნახატი.

ეს არის მაგალითი ამისთვის დამოუკიდებელი გადაწყვეტილება, ხსნარის ნიმუში გაკვეთილის ბოლოს.

მოდით გადავიდეთ ამოცანის ყველაზე პოპულარულ და გავრცელებულ ვერსიაზე, როდესაც ფუნქცია შედგება სამი ნაწილისგან:

მაგალითი 4

შეისწავლეთ ფუნქცია უწყვეტობისთვის და დახაზეთ ფუნქციის გრაფიკი .

გამოსავალი: აშკარაა, რომ ფუნქციის სამივე ნაწილი უწყვეტია შესაბამის ინტერვალებზე, ამიტომ რჩება მხოლოდ ნაწილებს შორის „შეერთების“ ორი წერტილის შემოწმება. პირველ რიგში, მოდით გავაკეთოთ ნახაზი, სტატიის პირველ ნაწილში საკმარისად დეტალურად გავამახვილე კომენტარი მშენებლობის ტექნიკაზე. ერთადერთი ის არის, რომ ყურადღებით უნდა მივყვეთ ჩვენს სინგულარულ წერტილებს: უტოლობის გამო, მნიშვნელობა მიეკუთვნება სწორ ხაზს (მწვანე წერტილი), ხოლო უტოლობის გამო, მნიშვნელობა ეკუთვნის პარაბოლას (წითელი წერტილი):


ისე, პრინციპში, ყველაფერი გასაგებია =) რჩება მხოლოდ გადაწყვეტილების ფორმირება. თითოეული ორი „შეერთების“ პუნქტისთვის ჩვენ სტანდარტულად ვამოწმებთ 3 უწყვეტობის პირობას:

მე)ჩვენ განვიხილავთ წერტილს უწყვეტობისთვის

1)

ცალმხრივი საზღვრები სასრული და განსხვავებულია, რაც ნიშნავს, რომ ფუნქცია განიცდის 1-ლი სახის შეწყვეტას წერტილში ნახტომით.

მოდით გამოვთვალოთ უწყვეტობის ნახტომი, როგორც განსხვავება მარჯვენა და მარცხენა ზღვრებს შორის:
ანუ, გრაფიკმა ერთი ერთეული აიწია.

II)ჩვენ განვიხილავთ წერტილს უწყვეტობისთვის

1) – ფუნქცია განსაზღვრულია მოცემულ წერტილში.

2) იპოვეთ ცალმხრივი საზღვრები:

- ცალმხრივი საზღვრები სასრული და თანაბარია, რაც ნიშნავს, რომ არსებობს ზოგადი ზღვარი.

3) – ფუნქციის ზღვარი წერტილში უდრის ამ ფუნქციის მნიშვნელობას მოცემულ წერტილში.

ფინალურ ეტაპზე ნახატს გადავიტანთ საბოლოო ვერსიაზე, რის შემდეგაც ვათავსებთ საბოლოო აკორდს:

უპასუხე: ფუნქცია უწყვეტია მთელ რიცხვთა წრფეზე, გარდა იმ წერტილისა, სადაც ის განიცდის პირველი სახის წყვეტას ნახტომით.

მაგალითი 5

შეისწავლეთ ფუნქცია უწყვეტობისთვის და შექმენით მისი გრაფიკი .

ეს არის მაგალითი დამოუკიდებელი გადაწყვეტისთვის, მოკლე ამოხსნისა და პრობლემის სავარაუდო ნიმუში გაკვეთილის ბოლოს.

შეიძლება გქონდეთ შთაბეჭდილება, რომ ერთ მომენტში ფუნქცია უნდა იყოს უწყვეტი, ხოლო მეორეში უნდა იყოს შეწყვეტა. პრაქტიკაში, ეს ყოველთვის ასე არ არის. შეეცადეთ არ უგულებელყოთ დარჩენილი მაგალითები - იქნება რამდენიმე საინტერესო და მნიშვნელოვანი თვისება:

მაგალითი 6

მოცემული ფუნქცია . გამოიკვლიეთ ფუნქცია წერტილებში უწყვეტობისთვის. შექმენით გრაფიკი.

გამოსავალი: და ისევ დაუყოვნებლივ შეასრულეთ ნახატი ნახატზე:

ამ გრაფიკის თავისებურება ის არის, რომ ცალი ფუნქცია მოცემულია აბსცისის ღერძის განტოლებით. ეს ტერიტორია აქ არის დახატული მწვანე, ხოლო რვეულში ის ჩვეულებრივ ხაზგასმულია თამამად უბრალო ფანქრით. და, რა თქმა უნდა, არ დაივიწყოთ ჩვენი ვერძები: მნიშვნელობა ეკუთვნის ტანგენტის ტოტს (წითელი წერტილი), ხოლო მნიშვნელობა ეკუთვნის სწორ ხაზს.

ნახაზიდან ყველაფერი ნათელია - ფუნქცია უწყვეტია მთელი რიცხვითი ხაზის გასწვრივ, რჩება მხოლოდ გადაწყვეტის ფორმალიზება, რომელიც სრულ ავტომატიზაციამდე მიდის სიტყვასიტყვით 3-4 მსგავსი მაგალითის შემდეგ:

მე)ჩვენ განვიხილავთ წერტილს უწყვეტობისთვის

1) – ფუნქცია განისაზღვრება მოცემულ წერტილში.

2) გამოვთვალოთ ცალმხრივი ლიმიტები:

, რაც ნიშნავს, რომ არსებობს ზოგადი ლიმიტი.

ყოველი შემთხვევისთვის შეგახსენებთ ტრივიალურ ფაქტს: მუდმივის ზღვარი უდრის თავად მუდმივას. ამ შემთხვევაში ნულის ზღვარი უდრის თავად ნულს (მარცხენა ლიმიტი).

3) – ფუნქციის ზღვარი წერტილში უდრის ამ ფუნქციის მნიშვნელობას მოცემულ წერტილში.

ამრიგად, ფუნქცია უწყვეტია წერტილში ფუნქციის უწყვეტობის განსაზღვრით წერტილში.

II)ჩვენ განვიხილავთ წერტილს უწყვეტობისთვის

1) – ფუნქცია განისაზღვრება მოცემულ წერტილში.

2) იპოვეთ ცალმხრივი საზღვრები:

და აქ - ერთის ზღვარი უდრის თავად ერთეულს.

- არსებობს ზოგადი ზღვარი.

3) – ფუნქციის ზღვარი წერტილში უდრის ამ ფუნქციის მნიშვნელობას მოცემულ წერტილში.

ამრიგად, ფუნქცია უწყვეტია წერტილში ფუნქციის უწყვეტობის განსაზღვრით წერტილში.

ჩვეულებისამებრ, კვლევის შემდეგ გადავიტანთ ჩვენს ნახატს საბოლოო ვერსიაზე.

უპასუხე: ფუნქცია უწყვეტია წერტილებში.

გთხოვთ გაითვალისწინოთ, რომ იმ პირობით, რომ ჩვენ არ გვკითხეს არაფერი უწყვეტობისთვის მთელი ფუნქციის შესწავლის შესახებ და ითვლება კარგ მათემატიკური ფორმად ფორმულირება ზუსტი და ნათელიპასუხი დასმულ კითხვაზე. სხვათა შორის, თუ პირობები არ მოითხოვს გრაფიკის შექმნას, მაშინ თქვენ გაქვთ სრული უფლება არ ააწყოთ იგი (თუმცა მოგვიანებით მასწავლებელს შეუძლია ამის გაკეთება გაიძულებთ).

პატარა მათემატიკური „ენის ტრიალი“ საკუთარი თავის გადასაჭრელად:

მაგალითი 7

მოცემული ფუნქცია . გამოიკვლიეთ ფუნქცია წერტილებში უწყვეტობისთვის. წყვეტის წერტილების კლასიფიკაცია, ასეთის არსებობის შემთხვევაში. შეასრულეთ ნახაზი.

სცადეთ ყველა „სიტყვის“ სწორად „გამოთქმა“ =) და უფრო ზუსტად დახაზეთ გრაფიკი, სიზუსტე, ყველგან ზედმეტი არ იქნება;-)

როგორც გახსოვთ, მე გირჩევდი ნახატის დაუყონებლივ დასრულებას მონახაზის სახით, მაგრამ დროდადრო ხვდები მაგალითებს, სადაც მაშინვე ვერ ხვდები, როგორ გამოიყურება გრაფიკი. ამიტომ, ზოგიერთ შემთხვევაში, ხელსაყრელია ჯერ ცალმხრივი საზღვრების პოვნა და მხოლოდ ამის შემდეგ, კვლევის საფუძველზე, ტოტების გამოსახვა. ბოლო ორ მაგალითში ჩვენ ასევე ვისწავლით რამდენიმე ცალმხრივი ლიმიტების გამოთვლის ტექნიკას:

მაგალითი 8

შეისწავლეთ ფუნქცია უწყვეტობისთვის და შექმენით მისი სქემატური გრაფიკი.

გამოსავალი: ცუდი წერტილები აშკარაა: (ამცირებს მაჩვენებლის მნიშვნელს ნულამდე) და (ამცირებს მთელი წილადის მნიშვნელს ნულამდე). გაურკვეველია, როგორ გამოიყურება ამ ფუნქციის გრაფიკი, რაც იმას ნიშნავს, რომ ჯობია ჯერ ჩაატაროთ კვლევა.

განმარტება. ფუნქცია f(x), რომელიც განსაზღვრულია x 0 წერტილის სიახლოვეს, ეწოდება უწყვეტი წერტილში x 0 თუ ფუნქციის ზღვარი და მისი მნიშვნელობა ამ ეტაპზე ტოლია, ე.ი.

ერთი და იგივე ფაქტი შეიძლება სხვანაირად დაიწეროს:

განმარტება. თუ ფუნქცია f(x) განსაზღვრულია x 0 წერტილის რომელიმე სამეზობლოში, მაგრამ არ არის უწყვეტი x 0 წერტილში, მაშინ მას ე.წ. ასაფეთქებელიფუნქცია და წერტილი x 0 არის შეწყვეტის წერტილი.

უწყვეტი ფუნქციის მაგალითი:

წ

0 x 0 - x 0 x 0 + x

პ უწყვეტი ფუნქციის მაგალითი:

განმარტება. f(x) ფუნქციას ეწოდება უწყვეტი x 0 წერტილში, თუ რომელიმე დადებითი რიცხვისთვის >0 არის რიცხვი >0 ისეთი, რომ ნებისმიერი x-ისთვის, რომელიც აკმაყოფილებს პირობას

უთანასწორობა მართალია
.

განმარტება. ფუნქცია f(x) ეწოდება უწყვეტი x = x 0 წერტილში, თუ ფუნქციის ზრდა x 0 წერტილში არის უსასრულოდ მცირე მნიშვნელობა.

f(x) = f(x 0) + (x)

სადაც (x) არის უსასრულოდ მცირე xx 0-ზე.

სადაც a(x) არის უსასრულოდ მცირე x®x0-ზე.

1) x 0 წერტილში უწყვეტი ფუნქციების ჯამი, სხვაობა და ნამრავლი არის x 0 წერტილში უწყვეტი ფუნქცია.

2) ორი უწყვეტი ფუნქციის კოეფიციენტი – არის უწყვეტი ფუნქცია იმ პირობით, რომ g(x) არ იყოს ნულის ტოლი x 0 წერტილში.

3) უწყვეტი ფუნქციების სუპერპოზიცია არის უწყვეტი ფუნქცია.

ეს ქონება შეიძლება ჩაიწეროს შემდეგნაირად:

თუ u = f(x), v = g(x) არის უწყვეტი ფუნქციები x = x 0 წერტილში, მაშინ ფუნქცია v = g(f(x)) ასევე უწყვეტი ფუნქციაა ამ წერტილში.

ზემოაღნიშნული თვისებების მართებულობა მარტივად შეიძლება დადასტურდეს ლიმიტის თეორემების გამოყენებით.

ზოგიერთი ელემენტარული ფუნქციის უწყვეტობა.

1) ფუნქცია f(x) = C, C = const არის უწყვეტი ფუნქცია განსაზღვრების მთელ დომენზე.

2) რაციონალური ფუნქცია
არის უწყვეტი x-ის ყველა მნიშვნელობისთვის, გარდა იმ მნიშვნელებისა, რომლებშიც მნიშვნელი ხდება ნული. ამრიგად, ამ ტიპის ფუნქცია უწყვეტია განსაზღვრების მთელ დომენში.

3) ტრიგონომეტრიული ფუნქციები sin და cos უწყვეტია მათი განმარტების სფეროში.

დავამტკიცოთ თვისება 3 ფუნქციისთვის y = sinx.

დავწეროთ y = sin(x + x) ფუნქციის ნამატი – sinx, ანუ გარდაქმნის შემდეგ:

მართლაც, არსებობს ლიმიტი ორი ფუნქციის პროდუქტისთვის
და
. ამ შემთხვევაში, კოსინუს ფუნქცია შეზღუდული ფუნქციააх0-ზე
და იმიტომ

სინუსური ფუნქციის ზღვარი
, მაშინ ის უსასრულოდ მცირეაх0-ზე.

ამრიგად, არსებობს შეზღუდული ფუნქციის ნამრავლი და უსასრულო მცირე, ამიტომ ეს ნამრავლი, ე.ი. ფუნქცია у არის უსასრულოდ მცირე. ზემოთ განხილული განმარტებების შესაბამისად, ფუნქცია y = sinx არის უწყვეტი ფუნქცია ნებისმიერი მნიშვნელობისთვის x = x 0 განმარტების დომენიდან, რადგან მისი ზრდა ამ ეტაპზე არის უსასრულო მცირე მნიშვნელობა.

შესვენების წერტილები და მათი კლასიფიკაცია.

განვიხილოთ ზოგიერთი ფუნქცია f(x), უწყვეტი x 0 წერტილის სიახლოვეს, ამ წერტილის შესაძლო გამონაკლისის გარდა. ფუნქციის წყვეტის წერტილის განმარტებიდან გამომდინარეობს, რომ x = x 0 არის წყვეტის წერტილი, თუ ფუნქცია არ არის განსაზღვრული ამ წერტილში ან არ არის უწყვეტი მასში.

ასევე უნდა აღინიშნოს, რომ ფუნქციის უწყვეტობა შეიძლება იყოს ცალმხრივი. მოდით ავხსნათ ეს შემდეგნაირად.

, მაშინ ამბობენ, რომ ფუნქცია არის სწორი უწყვეტი.

თუ ცალმხრივი ლიმიტი (იხ. ზემოთ)
, მაშინ ამბობენ, რომ ფუნქცია რჩება უწყვეტად.

განმარტება. წერტილი x 0 ეწოდება შესვენების წერტილიფუნქცია f(x), თუ f(x) არ არის განსაზღვრული x 0 წერტილში ან არ არის უწყვეტი ამ წერტილში.

განმარტება. წერტილი x 0 ეწოდება პირველი ტიპის შეწყვეტის წერტილი, თუ ამ მომენტში f(x) ფუნქციას აქვს სასრული, მაგრამ არა ტოლი, მარცხენა და მარჯვენა ზღვრები.

ამ განმარტების პირობების დასაკმაყოფილებლად არ არის აუცილებელი, რომ ფუნქცია განისაზღვროს x = x 0 წერტილში, საკმარისია ის განისაზღვროს მისგან მარცხნივ და მარჯვნივ.

განმარტებიდან შეგვიძლია დავასკვნათ, რომ 1-ლი სახის შეწყვეტის წერტილში ფუნქციას შეიძლება ჰქონდეს მხოლოდ სასრული ნახტომი. ზოგიერთ განსაკუთრებულ შემთხვევაში, 1-ლი ტიპის შეწყვეტის წერტილსაც ზოგჯერ უწოდებენ მოსახსნელიგადამწყვეტი წერტილი, მაგრამ ამაზე დაწვრილებით ქვემოთ ვისაუბრებთ.

განმარტება. წერტილი x 0 ეწოდება მე-2 ტიპის შეწყვეტის წერტილი, თუ ამ მომენტში f(x) ფუნქციას არ აქვს ცალმხრივი ზღვრებიდან ერთი მაინც ან ერთი მათგანი მაინც უსასრულოა.

ფუნქციის უწყვეტობა ინტერვალზე და სეგმენტზე.

განმარტება. ფუნქცია f(x) ეწოდება უწყვეტი ინტერვალზე (სეგმენტი), თუ იგი უწყვეტია ინტერვალის (სეგმენტის) ნებისმიერ წერტილში.

ამ შემთხვევაში, ფუნქციის უწყვეტობა სეგმენტის ან ინტერვალის ბოლოებში არ არის საჭირო.

ფუნქციების თვისებები უწყვეტი ინტერვალზე.

საკუთრება 1: (ვაიერშტრასის პირველი თეორემა (Carl Weierstrass (1815-1897) - გერმანელი მათემატიკოსი)). ფუნქცია, რომელიც უწყვეტია ინტერვალზე, შემოიფარგლება ამ ინტერვალზე, ე.ი. პირობა –M  f(x)  M დაკმაყოფილებულია სეგმენტზე.

ამ თვისების მტკიცებულება ემყარება იმ ფაქტს, რომ ფუნქცია, რომელიც უწყვეტია x 0 წერტილში, შემოიფარგლება მის გარკვეულ მიმდებარედ, და თუ სეგმენტს დაყოფთ უსასრულო რაოდენობის სეგმენტებად, რომლებიც „შეკუმშულია“ წერტილამდე. x 0, მაშინ იქმნება x 0 წერტილის გარკვეული მეზობლობა.

საკუთრება 2: ფუნქცია, რომელიც უწყვეტია სეგმენტზე, იღებს მასზე უდიდეს და უმცირეს მნიშვნელობებს.

იმათ. არის მნიშვნელობები x 1 და x 2 ისეთი, რომ f(x 1) = m, f(x 2) = M და

m  f(x)  M

იმათ. არსებობს მნიშვნელობები x1 და x2 ისეთი, რომ f(x1) = m, f(x2) = M და

სეგმენტზე ფუნქციის უდიდეს და უმცირეს მნიშვნელობას შორის განსხვავება ეწოდება ყოყმანიფუნქციონირებს სეგმენტზე.

საკუთრება 3: (მეორე ბოლზანო-კოშის თეორემა). ფუნქცია, რომელიც უწყვეტია ინტერვალზე, იღებს ყველა მნიშვნელობას ამ ინტერვალზე ორ თვითნებურ მნიშვნელობას შორის.

საკუთრება 4: თუ ფუნქცია f(x) უწყვეტია x = x 0 წერტილში, მაშინ არის x 0 წერტილის რაღაც სამეზობლო, რომელშიც ფუნქცია ინარჩუნებს თავის ნიშანს.

საკუთრება 5: (ბოლცანოს პირველი თეორემა (1781-1848) - კოში). თუ ფუნქცია f(x) უწყვეტია სეგმენტზე და აქვს საპირისპირო ნიშნების მნიშვნელობები სეგმენტის ბოლოებში, მაშინ ამ სეგმენტის შიგნით არის წერტილი, სადაც f(x) = 0.

იმათ. თუ ნიშანი(f(a))  ნიშანი(f(b)), მაშინ  x 0: f(x 0) = 0.

მაგალითი.

x = -1 წერტილში ფუნქცია უწყვეტია x = 1 ტიპის უწყვეტობის წერტილში

ზე

მაგალითი.შეისწავლეთ ფუნქცია უწყვეტობისთვის და განსაზღვრეთ შეწყვეტის წერტილების ტიპი, ასეთის არსებობის შემთხვევაში.

x = 0 წერტილში ფუნქცია უწყვეტია x = 1 ტიპის უწყვეტობის წერტილში