მთავარი

შუშის ფასადები

უსაზღვროდ დიდ ფუნქციებს აქვთ თავისი თვისებები. უსასრულოდ დიდი ფუნქციის განმარტება. უსასრულოდ მცირე ფუნქციები

უსაზღვროდ დიდ ფუნქციებს აქვთ თავისი თვისებები. უსასრულოდ დიდი ფუნქციის განმარტება. უსასრულოდ მცირე ფუნქციები

მოცემულია უსასრულოდ დიდი მიმდევრობის განმარტება. განიხილება უსასრულობის წერტილების სამეზობლოების ცნებები. მოცემულია მიმდევრობის ზღვრის უნივერსალური განმარტება, რომელიც ეხება როგორც სასრულ, ასევე უსასრულო ზღვრებს. განიხილება უსასრულოდ დიდი მიმდევრობის განმარტების გამოყენების მაგალითები.

შინაარსი

აგრეთვე იხილეთ: მიმდევრობის ლიმიტის განსაზღვრა

განმარტება

ქვემიმდევრობა (βn) უსასრულოდ დიდი თანმიმდევრობა ეწოდება, თუ რომელიმე M რიცხვისთვის, რაც არ უნდა დიდი იყოს, არსებობს ასეთი ბუნებრივი რიცხვი N M დამოკიდებულია M-ზე ისე, რომ ყველა ბუნებრივი n > N Mსთვის მოქმედებს შემდეგი უტოლობა:
|βn | >მ.
ამ შემთხვევაში წერენ
.
ან ზე.
ისინი ამბობენ, რომ ის მიდრეკილია უსასრულობისკენ, ან უსასრულობამდე იყრის თავს.

თუ რომელიმე რიცხვიდან N-დან დაწყებული 0 , ეს
( ემთხვევა პლუს უსასრულობას).
თუ მაშინ
( იყრის მინუს უსასრულობას).

მოდით დავწეროთ ეს განმარტებები არსებობისა და უნივერსალურობის ლოგიკური სიმბოლოების გამოყენებით:
(1) .
(2) .
(3) .

(2) და (3) საზღვრებით მიმდევრები არის უსასრულოდ დიდი მიმდევრობის განსაკუთრებული შემთხვევები (1). ამ განმარტებებიდან გამომდინარეობს, რომ თუ მიმდევრობის ზღვარი უდრის პლუს ან მინუს უსასრულობას, მაშინ ის ასევე უდრის უსასრულობას:
.
საპირისპირო, რა თქმა უნდა, არ შეესაბამება სიმართლეს. მიმდევრობის წევრებს შეიძლება ჰქონდეთ მონაცვლეობითი ნიშნები. ამ შემთხვევაში, ლიმიტი შეიძლება იყოს უსასრულობის ტოლი, მაგრამ კონკრეტული ნიშნის გარეშე.

გაითვალისწინეთ ისიც, რომ თუ რაიმე თვისება მოქმედებს თვითნებურ მიმდევრობაზე უსასრულობის ტოლი ლიმიტით, მაშინ იგივე თვისება მოქმედებს მიმდევრობისთვის, რომლის ზღვარი უდრის პლუსს ან მინუს უსასრულობას.

გაანგარიშების ბევრ სახელმძღვანელოში, უსასრულოდ დიდი მიმდევრობის განმარტება ამბობს, რომ რიცხვი M დადებითია: M > 0 .

თუმცა, ეს მოთხოვნა არასაჭიროა. თუ ის გაუქმებულია, მაშინ არანაირი წინააღმდეგობა არ წარმოიქმნება. უბრალოდ, მცირე თუ ნეგატიური ღირებულებები ჩვენთვის არ არის საინტერესო. ჩვენ გვაინტერესებს მიმდევრობის ქცევა M-ის თვითნებურად დიდი დადებითი მნიშვნელობებისთვის. > 0 ამიტომ, თუ გაჩნდება საჭიროება, მაშინ M შეიძლება შემოიფარგლოს ქვემოდან ნებისმიერი წინასწარ განსაზღვრული რიცხვით a, ანუ შეგვიძლია ვივარაუდოთ, რომ M > a.

როდესაც ჩვენ განვსაზღვრეთ ε - ბოლო წერტილის მეზობლობა, მაშინ მოთხოვნა ε

მნიშვნელოვანია. უარყოფითი მნიშვნელობებისთვის უთანასწორობა საერთოდ ვერ დაკმაყოფილდება.

წერტილების სამეზობლოები უსასრულობაში
როდესაც განვიხილეთ სასრული საზღვრები, ჩვენ შემოვიღეთ წერტილის მეზობლობის კონცეფცია. შეგახსენებთ, რომ ბოლო წერტილის სამეზობლო არის ღია ინტერვალი, რომელიც შეიცავს ამ წერტილს. ჩვენ ასევე შეგვიძლია შემოვიტანოთ უსასრულობის წერტილების სამეზობლოების კონცეფცია.მოდით M იყოს თვითნებური რიცხვი.
წერტილის "უსასრულობის" მეზობლობამოდით M იყოს თვითნებური რიცხვი.
, , კომპლექტი ეწოდება.მოდით M იყოს თვითნებური რიცხვი.

წერტილის მეზობლობა "პლუს უსასრულობა"
(4) ,
წერტილის სიახლოვეს "მინუს უსასრულობა" 1 მკაცრად რომ ვთქვათ, "უსასრულობის" წერტილის მეზობლობა არის კომპლექტი 2 სადაც მ

და მ

- თვითნებური დადებითი რიცხვები. ჩვენ გამოვიყენებთ პირველ განმარტებას, რადგან ის უფრო მარტივია. თუმცა, ყველაფერი, რაც ქვემოთ არის ნათქვამი, ასევე მართალია განმარტების გამოყენებისას (4)..
ახლა ჩვენ შეგვიძლია მივცეთ მიმდევრობის ზღვრის ერთიანი განმარტება, რომელიც ეხება როგორც სასრულ, ასევე უსასრულო ზღვრებს.

მიმდევრობის ლიმიტის უნივერსალური განმარტება

წერტილი a (სასრული ან უსასრულობაში) არის მიმდევრობის ზღვარი, თუ ამ წერტილის რომელიმე სამეზობლოსთვის არის ნატურალური რიცხვი N ისეთი, რომ რიცხვებით მიმდევრობის ყველა ელემენტი ეკუთვნის ამ მეზობელს.
ამრიგად, თუ ლიმიტი არსებობს, მაშინ a წერტილის მიმდებარედ შეიძლება იყოს მხოლოდ მიმდევრობის წევრების სასრული რაოდენობა, ან ცარიელი სიმრავლე. ეს პირობა აუცილებელი და საკმარისია. ამ თვისების მტკიცებულება ზუსტად იგივეა, რაც სასრული ზღვრებისთვის.
კონვერგენტული მიმდევრობის სამეზობლო თვისება

იმისთვის, რომ წერტილი a (სასრულო ან უსასრულობაში) იყოს მიმდევრობის ზღვარი, აუცილებელია და საკმარისია, რომ ამ წერტილის რომელიმე მახლობლად არსებობდეს მიმდევრობის ტერმინების სასრული რაოდენობა ან ცარიელი სიმრავლე.
მტკიცებულება .
ასევე ზოგჯერ შემოდის ε - უსასრულობის წერტილების მეზობლების ცნებები. შეგახსენებთ, რომ a სასრულ წერტილის ε-მეზობლობა არის სიმრავლე.. ე აღვნიშნოთ a წერტილის მეზობლობა.
.
შემდეგ ბოლო წერტილისთვის,
;
;
.
უსასრულობის წერტილებისთვის:

ε-მეზობლების ცნებების გამოყენებით, შეგვიძლია მივცეთ მიმდევრობის ზღვრის კიდევ ერთი უნივერსალური განმარტება: წერტილი a (ტერმინალი ან უსასრულობა) არის მიმდევრობის ზღვარი, თუ ასეთია ε > 0 დადებითი რიცხვი
.

არსებობს ნატურალური რიცხვი N ε, რომელიც დამოკიდებულია ε-ზე ისეთი, რომ ყველა რიცხვისთვის n > N ε ტერმინები x n მიეკუთვნება a წერტილის ε-მეზობელს:
.

არსებობისა და უნივერსალურობის ლოგიკური სიმბოლოების გამოყენებით, ეს განმარტება შეიძლება დაიწეროს შემდეგნაირად:

უსასრულოდ დიდი თანმიმდევრობის მაგალითები

.
მაგალითი 1
(1) .
მოდით ჩამოვწეროთ უსასრულოდ დიდი მიმდევრობის განმარტება:
.

ჩვენს შემთხვევაში
.
ჩვენ ვაცნობთ რიცხვებს და , მათ უტოლობასთან ვაკავშირებთ:
.
უტოლობების თვისებების მიხედვით, თუ და , მაშინ
გაითვალისწინეთ, რომ ეს უტოლობა მოქმედებს ნებისმიერი n-ისთვის.
ამიტომ, შეგიძლიათ აირჩიოთ ასე:

ზე ;
.
ზე.

ასე რომ, ნებისმიერისთვის შეგვიძლია ვიპოვოთ ნატურალური რიცხვი, რომელიც აკმაყოფილებს უტოლობას.

მაშინ ყველასთვის,
.

(2) .
ეს იმას ნიშნავს, რომ.
.

ანუ თანმიმდევრობა უსასრულოდ დიდია.
.
.

მაგალითი 2
.
უსასრულოდ დიდი მიმდევრობის განმარტების გამოყენებით, აჩვენე ეს

მოცემული თანმიმდევრობის ზოგად ტერმინს აქვს ფორმა:

მაშინ ყველასთვის,
.

შეიყვანეთ ნომრები და:
(3) .
ეს იმას ნიშნავს, რომ.
.

ანუ თანმიმდევრობა უსასრულოდ დიდია.
.
მაშინ ნებისმიერს შეუძლია იპოვოთ ნატურალური რიცხვი, რომელიც აკმაყოფილებს უტოლობას, ასე რომ, ყველასთვის,
.

ეს იმას ნიშნავს, რომ.
.

მაგალითი 3
.

მოდით ჩამოვწეროთ მინუს უსასრულობის ტოლი მიმდევრობის ზღვრის განმარტება:

მაშინ ყველასთვის,
.

აქედან ირკვევა, რომ თუ და, მაშინ
.
ვინაიდან ნებისმიერისთვის შესაძლებელია ნატურალური რიცხვის პოვნა, რომელიც აკმაყოფილებს უტოლობას, მაშინ
(2) .

მოცემული, როგორც N, შეგვიძლია ავიღოთ ნებისმიერი ნატურალური რიცხვი, რომელიც აკმაყოფილებს შემდეგ უტოლობას: = 1, 2, 3, ... , ეს
;
;
.

მაგალითი 4
.
მაშინ ნებისმიერს შეუძლია იპოვოთ ნატურალური რიცხვი, რომელიც აკმაყოფილებს უტოლობას, ასე რომ, ყველასთვის,
.

მოდით დავწეროთ თანმიმდევრობის ზოგადი ტერმინი:
.
უსასრულოდ დიდი მიმდევრობის განმარტების გამოყენებით, აჩვენე ეს

მოდით ჩამოვწეროთ მიმდევრობის ზღვრის განმარტება პლუს უსასრულობის ტოლი:
ვინაიდან n ნატურალური რიცხვია, n
ჩვენ ვაცნობთ რიცხვებს და M-ს, ვაკავშირებთ მათ უტოლობებთან:

ასე რომ, ნებისმიერი M რიცხვისთვის შეგვიძლია ვიპოვოთ ნატურალური რიცხვი, რომელიც აკმაყოფილებს უტოლობას.

მაშინ ყველასთვის, გამოყენებული ლიტერატურა:ლ.დ. კუდრიავცევი. მათემატიკური ანალიზის კურსი. ტომი 1. მოსკოვი, 2003 წ. CM. ნიკოლსკი. მათემატიკური ანალიზის კურსი. ტომი 1. მოსკოვი, 1983 წ.აგრეთვე იხილეთ: ფუნქცია y=f(x) დაურეკაუსასრულოდ მცირე ზე x→a

ან როდის

x →∞, თუ ან , ე.ი. უსასრულოდ=(დაურეკამცირე ფუნქცია დაურეკაარის ფუნქცია, რომლის ზღვარი მოცემულ წერტილში არის ნული.

მაგალითები. →∞, თუ ან , ე.ი. უსასრულოდ 1. ფუნქცია დაურეკა f(x) დაურეკა→0.

3. →∞, თუ ან , ე.ი. უსასრულოდ-1) 2 არის უსასრულოდ მცირე დაურეკა→1, ვინაიდან (იხ. სურათი). დაურეკა→0.

4. →∞, თუ ან , ე.ი. უსასრულოდ = 1/დაურეკა 2. ფუნქცია დაურეკა→∞.

მოდით დავამყაროთ შემდეგი მნიშვნელოვანი ურთიერთობა:

თეორემა.თუ ფუნქცია გამოყენებული ლიტერატურა:წარმომადგენლობით ფუნქციამუდმივი რიცხვის ჯამის სახით ბდა უსასრულოდ მცირე სიდიდე α(x): f (x)=b+ α(x)რომ .

პირიქით, თუ, მაშინ f (x)=b+α(x), სად a(x) f(x) x→a.

მტკიცებულება.

1. დავამტკიცოთ განცხადების პირველი ნაწილი. თანასწორობიდან f(x)=b+α(x)უნდა |f(x) – b|=| α|. მაგრამ მას შემდეგ a(x)არის უსასრულოდ მცირე, მაშინ თვითნებური ε-სთვის არის δ – წერტილის სამეზობლო ა,ყველას თვალწინ დაურეკასაიდანაც, ღირებულებები a(x)დააკმაყოფილოს ურთიერთობა |α(x)|< ე. მერე |f(x) – b|< ე. და ეს იმას ნიშნავს.

2. თუ , მაშინ ნებისმიერი ε >0 ყველასთვის Xზოგიერთი δ – წერტილის მეზობლობა ანება |f(x) – b|< ე. მაგრამ თუ აღვნიშნავთ f(x) – b= α, ეს |α(x)|< ε, რაც იმას ნიშნავს ა- უსასრულოდ მცირე.

განვიხილოთ უსასრულოდ მცირე ფუნქციების ძირითადი თვისებები.

თეორემა 1.ორი, სამი და ზოგადად ნებისმიერი სასრული რაოდენობის უსასრულო რიცხვის ალგებრული ჯამი უსასრულო მცირე ფუნქციაა.

მტკიცებულება. მოდით დავამტკიცოთ ორი ტერმინი. დაე f(x)=α(x)+β(x), სად და. ჩვენ უნდა დავამტკიცოთ, რომ თვითნებურად მცირე ε > ნაპოვნია 0 δ> 0, ისეთი, რომ ამისთვის დაურეკა, უთანასწორობის დაკმაყოფილება |x – a|<δ , შესრულებულია |f(x)|< ε.

მაშ ასე, დავაფიქსიროთ თვითნებური რიცხვი ε > 0. ვინაიდან თეორემის პირობების მიხედვით α(x)არის უსასრულოდ მცირე ფუნქცია, მაშინ არის ასეთი δ 1 > 0, რაც არის |x – a|< δ 1 გვაქვს |α(x)|< ε / 2. ანალოგიურად, მას შემდეგ β(x)არის უსასრულოდ მცირე, მაშინ არის ასეთი δ 2 > 0, რაც არის |x – a|< δ 2 გვაქვს | β(x)|< ε / 2.

ავიღოთ δ=წთ(δ 1 , δ2 } .მერე პუნქტის სიახლოვეს არადიუსი δ თითოეული უტოლობა დაკმაყოფილდება |α(x)|< ε / 2 და | β(x)|< ε / 2. ამიტომ, ამ სამეზობლოში იქნება

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

იმათ. |f(x)|< ε, რაც დასამტკიცებელია.

თეორემა 2.უსასრულოდ მცირე ფუნქციის პროდუქტი a(x)შეზღუდული ფუნქციისთვის →∞, თუ ან , ე.ი. უსასრულოდაგრეთვე იხილეთ: ფუნქცია(ან როდის x→∞) არის უსასრულოდ მცირე ფუნქცია.

მტკიცებულება. ფუნქციიდან გამომდინარე →∞, თუ ან , ე.ი. უსასრულოდშეზღუდულია, მაშინ არის რაოდენობა მისეთი, რომ ყველა ღირებულებისთვის დაურეკაწერტილის რომელიღაც უბნიდან a|f(x)|≤M.უფრო მეტიც, მას შემდეგ a(x)არის უსასრულოდ მცირე ფუნქცია at ფუნქცია, შემდეგ თვითნებური ε > 0 არის წერტილის სამეზობლო ა, რომელშიც უთანასწორობა შენარჩუნდება |α(x)|< ε /მ. შემდეგ ამ უბნებიდან უფრო პატარა გვაქვს | αf|< ε /მ= ე. და ეს იმას ნიშნავს აფ- უსასრულოდ მცირე. შემთხვევისთვის x→∞მტკიცებულება ხორციელდება ანალოგიურად.

დადასტურებული თეორემიდან გამომდინარეობს:

დასკვნა 1.თუ და, მაშინ.

დასკვნა 2.თუ და c=კონსტ, მაშინ.

თეორემა 3.უსასრულოდ მცირე ფუნქციის თანაფარდობა α(x)თითო ფუნქციაზე →∞, თუ ან , ე.ი. უსასრულოდ, რომლის ზღვარი განსხვავდება ნულისაგან, არის უსასრულოდ მცირე ფუნქცია.

მტკიცებულება. დაე . შემდეგ 1 /f(x)არის შეზღუდული ფუნქცია. მაშასადამე, წილადი არის უსასრულოდ მცირე ფუნქციისა და შეზღუდული ფუნქციის ნამრავლი, ე.ი. ფუნქცია უსასრულოდ მცირეა.

უსასრულო და დიდის გამოთვლა

უსასრულოდ მცირე გაანგარიშება- უსასრულო სიდიდეებით შესრულებული გამოთვლები, რომლებშიც მიღებული შედეგი განიხილება როგორც უსასრულო მცირეთა უსასრულო ჯამი. უსასრულოდ მცირე გაანგარიშება არის ზოგადი კონცეფციადიფერენციალური და ინტეგრალური გამოთვლებისთვის, რომლებიც ქმნიან თანამედროვე უმაღლესი მათემატიკის საფუძველს. უსასრულო სიდიდის ცნება მჭიდროდაა დაკავშირებული ლიმიტის ცნებასთან.

უსასრულოდ მცირე

ქვემიმდევრობა ა ნდაურეკა CM. ნიკოლსკი. მათემატიკური ანალიზის კურსი. ტომი 1. მოსკოვი, 1983 წ., თუ . მაგალითად, რიცხვების თანმიმდევრობა უსასრულოდ მცირეა.

ფუნქციას ეძახიან უსასრულოდ მცირე წერტილის სიახლოვეს დაურეკა 0 თუ .

ფუნქციას ეძახიან უსასრულოდ მცირე უსასრულობაში, თუ ან .

ასევე უსასრულოდ მცირე არის ფუნქცია, რომელიც არის განსხვავება ფუნქციასა და მის ზღვარს შორის, ანუ თუ , ეს ვ(დაურეკა) − ა = α( დაურეკა) , .

უსაზღვროდ დიდი რაოდენობით

ქვემიმდევრობა ა ნდაურეკა უსასრულოდ დიდი, თუ .

ფუნქციას ეძახიან უსასრულოდ დიდი წერტილის სიახლოვეს დაურეკა 0 თუ .

ფუნქციას ეძახიან უსასრულოდ დიდი უსასრულობაში, თუ ან .

ყველა შემთხვევაში, უსასრულობა თანასწორობის უფლებით იგულისხმება გარკვეული ნიშნით (ან „პლუს“ ან „მინუს“). ეს არის, მაგალითად, ფუნქცია დაურეკაცოდვა დაურეკაარ არის უსასრულოდ დიდი at.

უსასრულოდ მცირე და უსასრულოდ დიდის თვისებები

უსასრულო მცირეთა შედარება

როგორ შევადაროთ უსასრულოდ მცირე რაოდენობა?
უსასრულო სიდიდეების თანაფარდობა ქმნის ე.წ.

განმარტებები

დავუშვათ, გვაქვს უსასრულო მცირე მნიშვნელობები α( დაურეკა) და β( დაურეკა) (ან, რაც არ არის მნიშვნელოვანი განმარტებისთვის, უსასრულოდ მცირე მიმდევრობები).

ასეთი ლიმიტების გამოსათვლელად მოსახერხებელია L'Hopital-ის წესის გამოყენება.

შედარების მაგალითები

გამოყენება შესახებ-სიმბოლიკა, მიღებული შედეგები შეიძლება ჩაიწეროს შემდეგი ფორმით დაურეკა 5 = ო(დაურეკა 3). IN ამ შემთხვევაშიჩანაწერები სწორია 2დაურეკა 2 + 6დაურეკა = ო(დაურეკა) და დაურეკა = ო(2დაურეკა 2 + 6დაურეკა).

ექვივალენტური მნიშვნელობები

განმარტება

თუ , მაშინ α და β უსასრულო სიდიდეებს უწოდებენ ექვივალენტი ().
აშკარაა, რომ ეკვივალენტური სიდიდეები არის ერთი და იგივე სიმცირის რიგის უსასრულო სიდიდის განსაკუთრებული შემთხვევა.

როდესაც შემდეგი ეკვივალენტური მიმართებები მოქმედებს: , , .

თეორემა

ორი უსასრულო სიდიდის კოეფიციენტის (ფარდობის) ზღვარი არ შეიცვლება, თუ ერთი მათგანი (ან ორივე) შეიცვლება ეკვივალენტური რაოდენობით..

ამ თეორემას აქვს პრაქტიკული მნიშვნელობა ლიმიტების პოვნისას (იხ. მაგალითი).

გამოყენების მაგალითი

ჩანაცვლება სმენ 2დაურეკა ექვივალენტური ღირებულება 2 დაურეკა, ვიღებთ

ისტორიული ჩანახატი

"უსასრულოდ მცირე" კონცეფცია განიხილებოდა ჯერ კიდევ ძველ დროში განუყოფელი ატომების კონცეფციასთან დაკავშირებით, მაგრამ არ იყო შეტანილი კლასიკურ მათემატიკაში. იგი კვლავ აღორძინდა მე-16 საუკუნეში „განყოფის მეთოდის“ მოსვლასთან ერთად - შესასწავლი ფიგურის დაყოფა უსასრულოდ მცირე მონაკვეთებად.

მე-17 საუკუნეში მოხდა უსასრულოდ მცირე გამოთვლების ალგებრიზაცია. მათი განსაზღვრა დაიწყეს, როგორც რიცხვითი სიდიდეები, რომლებიც ნაკლებია ნებისმიერ სასრულ (არანულოვან) სიდიდეზე და მაინც არ არის ნულის ტოლი. ანალიზის ხელოვნება მდგომარეობდა უსასრულო მცირე ზომის (დიფერენციალების) შემცველი მიმართების შედგენაში და შემდეგ მის ინტეგრირებაში.

ძველი სკოლის მათემატიკოსებმა ეს კონცეფცია გამოსცადეს უსასრულოდ მცირემკაცრი კრიტიკა. მიშელ როლელმა დაწერა, რომ ახალი გაანგარიშება არის " გენიალური შეცდომების ნაკრები"; ვოლტერმა კაზუსულად აღნიშნა, რომ გაანგარიშება არის ნივთების გამოთვლისა და ზუსტად გაზომვის ხელოვნება, რომელთა არსებობის დამტკიცება შეუძლებელია. ჰაიგენსმაც კი აღიარა, რომ მას არ ესმოდა უმაღლესი რანგის დიფერენციალურობის მნიშვნელობა.

ბედის ირონიად შეიძლება ჩაითვალოს არასტანდარტული ანალიზის საუკუნის შუა ხანებში გაჩენა, რამაც დაამტკიცა, რომ თავდაპირველი თვალსაზრისი - ფაქტობრივი უსასრულო - ასევე თანმიმდევრული იყო და შეიძლება გამოეყენებინათ ანალიზისთვის.

აგრეთვე იხილეთ

ფონდი ვიკიმედია.

2010 წელი.

ნახეთ, რა არის „უსასრულოდ დიდი“ სხვა ლექსიკონებში: ცვლადი რაოდენობა Y არის უსასრულოდ მცირე რაოდენობის X-ის შებრუნებული, ანუ Y = 1/X...

დიდი ენციკლოპედიური ლექსიკონი ცვლადი y არის უსასრულო x-ის შებრუნებული, ანუ y = 1/x. * * * უსასრულოდ დიდი უსასრულოდ დიდი, ცვლადი რაოდენობა Y, შებრუნებული უსასრულოდ მცირე რაოდენობით X, ანუ Y = 1/X ...

ენციკლოპედიური ლექსიკონი მათემატიკაში ცვლადი სიდიდე, რომელიც ცვლილების მოცემულ პროცესში ხდება და რჩება ნებისმიერ წინასწარ განსაზღვრულ რიცხვზე მეტი აბსოლუტური მნიშვნელობით. შესწავლა ბ.ბ. რაოდენობები შეიძლება შემცირდეს უსასრულო მცირეების შესასწავლად (იხ.... ...

დიდი საბჭოთა ენციკლოპედია

მაშინ ყველასთვის, გამოყენებული ლიტერატურა:ლ.დ. კუდრიავცევი. მათემატიკური ანალიზის კურსი. ტომი 1. მოსკოვი, 2003 წ. უსასრულო პატარა ფუნქციები და მათი ძირითადი თვისებებიაგრეთვე იხილეთ: ფუნქცია y=f(x) დაურეკაუსასრულოდ მცირე

ან როდის

მოდით დავამყაროთ შემდეგი მნიშვნელოვანი ურთიერთობა:

თეორემა.თუ ფუნქცია გამოყენებული ლიტერატურა:→∞, თუ ან , ე.ი. უსასრულოდ მცირე ფუნქცია არის ფუნქცია, რომლის ზღვარი მოცემულ წერტილში არის ნული. ფუნქციამუდმივი რიცხვის ჯამის სახით ბწარმომადგენლობით α(x): f (x)=b+ α(x)და უსასრულოდ მცირე სიდიდე

რომ . f (x)=b+α(x)პირიქით, თუ, მაშინ a(x), სად x→a.

მტკიცებულება.

– უსასრულოდ მცირე ზე

თეორემა 1.განვიხილოთ უსასრულოდ მცირე ფუნქციების ძირითადი თვისებები.

მტკიცებულებაორი, სამი და ზოგადად ნებისმიერი სასრული რაოდენობის უსასრულო რიცხვის ალგებრული ჯამი უსასრულო მცირე ფუნქციაა. f(x)=α(x)+β(x). მოდით დავამტკიცოთ ორი ტერმინი. დაე > , სად და. ჩვენ უნდა დავამტკიცოთ, რომ თვითნებურად მცირე ε δ> ნაპოვნია 0 დაურეკა 0, ისეთი, რომ ამისთვის |x – a|<δ , შესრულებულია |f(x)|< ε.

, უთანასწორობის დაკმაყოფილება > 0. ვინაიდან თეორემის პირობების მიხედვით α(x)მაშ ასე, დავაფიქსიროთ თვითნებური რიცხვი ε > არის უსასრულოდ მცირე ფუნქცია, მაშინ არის ასეთი δ 1 |x – a|< δ 1 გვაქვს |α(x)|< ε / 2. ანალოგიურად, მას შემდეგ β(x) 0, რაც არის > არის უსასრულოდ მცირე ფუნქცია, მაშინ არის ასეთი δ 1 |x – a|< δ 2 გვაქვს | β(x)|< ε / 2.

ავიღოთ δ=წთ(δ 1 , δ2 } .მერე პუნქტის სიახლოვეს არადიუსი δ არის უსასრულოდ მცირე, მაშინ არის ასეთი δ 2 |α(x)|< ε / 2 და | β(x)|< ε / 2. თითოეული უტოლობა დაკმაყოფილდება

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

იმათ. |f(x)|< ε, რაც დასამტკიცებელია.

თეორემა 2.უსასრულოდ მცირე ფუნქციის პროდუქტი a(x)შეზღუდული ფუნქციისთვის →∞, თუ ან , ე.ი. უსასრულოდზე ფუნქცია(ან როდის x→∞) არის უსასრულოდ მცირე ფუნქცია.

დადასტურებული თეორემიდან გამომდინარეობს:

დასკვნა 1.თუ და, მაშინ.

დასკვნა 2.თუ და c=კონსტ, მაშინ.

მტკიცებულება. დაე . შემდეგ 1 /f(x)არის შეზღუდული ფუნქცია. ამიტომ წილადი არის უსასრულოდ მცირე ფუნქციისა და შეზღუდული ფუნქციის ნამრავლი, ე.ი. ფუნქცია უსასრულოდ მცირეა.

უსასრულოდ მცირე და უსასრულოდ დიდ ფუნქციებს შორის ურთიერთობა

თეორემა 1.თუ ფუნქცია →∞, თუ ან , ე.ი. უსასრულოდარის უსასრულოდ დიდი at ფუნქცია, შემდეგ ფუნქცია 1 /f(x)არის უსასრულოდ მცირე ფუნქცია.

მტკიცებულება.ავიღოთ თვითნებური რიცხვი ε >0 და აჩვენე ეს ზოგიერთს δ>0 (დამოკიდებულია ε) ყველასთვის დაურეკა, რისთვისაც |x – a|<δ , უთანასწორობა დაკმაყოფილებულია და ეს იმას ნიშნავს 1/f(x)უსასრულოდ მცირე ფუნქციაა. მართლაც, მას შემდეგ →∞, თუ ან , ე.ი. უსასრულოდარის უსასრულოდ დიდი ფუნქცია ფუნქცია, მაშინ იქნება δ>0 ისეთი რომ როგორც კი |x – a|<δ , ასე | f(x)|> 1/ ე. მაგრამ შემდეგ იგივე დაურეკა.

ან როდის

საპირისპირო თეორემაც შეიძლება დადასტურდეს.

თეორემა 2.თუ ფუნქცია →∞, თუ ან , ე.ი. უსასრულოდ- უსასრულოდ მცირე ზე ფუნქცია(ან x→∞)და არ ქრება, მაშინ y= 1/f(x)უსასრულოდ დიდი ფუნქციაა.

თავად ჩაატარეთ თეორემის დადასტურება.

ან როდის

ამრიგად, უსასრულოდ მცირე და უსასრულოდ დიდი ფუნქციების უმარტივესი თვისებები შეიძლება ჩაიწეროს შემდეგი პირობითი ურთიერთობების გამოყენებით: ა≠ 0

ლიმიტის თეორემები

თეორემა 1.ორი, სამი და საერთოდ ფუნქციების გარკვეული რაოდენობის ალგებრული ჯამის ზღვარი უდრის ამ ფუნქციების ზღვრების ალგებრულ ჯამს, ე.ი.

მტკიცებულება. მოდით განვახორციელოთ მტკიცებულება ორი ტერმინისთვის, რადგან ეს შეიძლება გაკეთდეს იმავე გზით ნებისმიერი რაოდენობის ტერმინისთვის. დაე .მაშინ f(x)=b+α(x)და g(x)=c+β(x)პირიქით, თუ, მაშინ α და β - უსასრულოდ მცირე ფუნქციები. აქედან გამომდინარე,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

იმიტომ რომ ბ+გარის მუდმივი და α(x) + β(x)არის უსასრულოდ მცირე ფუნქცია, მაშინ

მაგალითი. .

თეორემა 2.ორი, სამი და ზოგადად სასრული რაოდენობის ფუნქციების ნამრავლის ზღვარი ტოლია ამ ფუნქციების ზღვრების ნამრავლის:

მტკიცებულება. დაე . აქედან გამომდინარე, f(x)=b+α(x)და g(x)=c+β(x)და

fg = (b + α) (c + β) = bc + (bβ + cα + αβ).

მუშაობა ძვ.წარის მუდმივი მნიშვნელობა. ფუნქცია bβ + c α + αβუსასრულოდ მცირე ფუნქციების თვისებებიდან გამომდინარე, არსებობს უსასრულო სიდიდე. ამიტომაც .

დასკვნა 1.მუდმივი ფაქტორი შეიძლება იქნას აღებული ლიმიტის ნიშნის მიღმა:

დასკვნა 2.ხარისხის ლიმიტი ძალაუფლების ტოლილიმიტი:

მაგალითი..

თეორემა 3.ორი ფუნქციის კოეფიციენტის ზღვარი ტოლია ამ ფუნქციების ზღვრების კოეფიციენტის, თუ მნიშვნელის ზღვარი განსხვავდება ნულისაგან, ე.ი.

მტკიცებულება. დაე . აქედან გამომდინარე, f(x)=b+α(x)და g(x)=c+β(x), სად α, β - უსასრულოდ მცირე. განვიხილოთ კოეფიციენტი

წილადი უსასრულოდ მცირე ფუნქციაა, რადგან მრიცხველი უსასრულო მცირე ფუნქციაა და მნიშვნელს აქვს ზღვარი. c 2 ≠0.

ან როდის

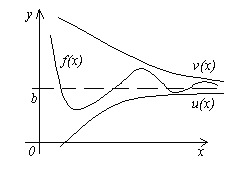
თეორემა 4.მიეცით სამი ფუნქცია f(x), u(x)და v(x), უტოლობების დაკმაყოფილება u (x)≤f(x)≤ v(x). თუ ფუნქციები u(x)და v(x)აქვს იგივე ლიმიტი ფუნქცია(ან x→∞), შემდეგ ფუნქცია →∞, თუ ან , ე.ი. უსასრულოდმიდრეკილია იმავე ზღვარზე, ე.ი. თუ

, რომ .

ამ თეორემის მნიშვნელობა ნათელია ფიგურიდან.

თეორემა 4-ის დადასტურება შეგიძლიათ ნახოთ, მაგალითად, სახელმძღვანელოში: Piskunov N. S. Differential and Integral Calculus, ტ. 1 - M.: Nauka, 1985 წ.

თეორემა 5.თუ ზე ფუნქცია(ან x→∞) ფუნქცია გამოყენებული ლიტერატურა:იღებს არაუარყოფით მნიშვნელობებს y≥0და ამავე დროს მიდრეკილია ზღვრამდე ბ, მაშინ ეს ზღვარი არ შეიძლება იყოს უარყოფითი: b≥0.

მტკიცებულება. ჩვენ მტკიცებულებას განვახორციელებთ წინააღმდეგობით. დავუშვათ, რომ ბ<0 , მაშინ |y – b|≥|b|და, შესაბამისად, განსხვავების მოდული არ არის ნულისკენ მიდრეკილი, როდესაც ფუნქცია. მაგრამ მერე წარ აღწევს ზღვარს ბაგრეთვე იხილეთ: ფუნქცია, რაც ეწინააღმდეგება თეორემის პირობებს.

თეორემა 6.თუ ორი ფუნქცია →∞, თუ ან , ე.ი. უსასრულოდდა g(x)არგუმენტის ყველა მნიშვნელობისთვის დაურეკადააკმაყოფილეთ უთანასწორობა f(x)≥ g(x)და აქვს ლიმიტები, მაშინ უთანასწორობა მოქმედებს b≥c.

მტკიცებულება.თეორემის პირობების მიხედვით f(x)-g(x) ≥0მაშასადამე, თეორემა 5-ით , ან .

ცალმხრივი ლიმიტები

აქამდე განვიხილეთ ფუნქციის ლიმიტის განსაზღვრა, როდესაც ფუნქციათვითნებურად, ე.ი. ფუნქციის ლიმიტი არ იყო დამოკიდებული იმაზე, თუ როგორ მდებარეობდა იგი დაურეკამიმართებაში ა, მარცხნივ ან მარჯვნივ ა. თუმცა, საკმაოდ ხშირია ფუნქციების პოვნა, რომლებსაც არ აქვთ ლიმიტი ამ პირობით, მაგრამ მათ აქვთ ლიმიტი თუ ფუნქცია, რჩება ერთ მხარეს ამარცხნივ ან მარჯვნივ (იხ. სურათი). აქედან გამომდინარე, შემოღებულია ცალმხრივი ლიმიტების ცნებები.

თუ →∞, თუ ან , ე.ი. უსასრულოდმიდრეკილია ზღვრამდე ბაგრეთვე იხილეთ: დაურეკათენდება გარკვეული რიცხვისკენ აასე რომ დაურეკაიღებს მხოლოდ მნიშვნელობებს ნაკლები ა, მერე წერენ და ურეკავენ f(x) ფუნქციის ბლიმიტი a წერტილში მარცხნივ.

უსასრულო და დიდის გამოთვლა

უსასრულოდ მცირე გაანგარიშება- უსასრულო სიდიდეებით შესრულებული გამოთვლები, რომლებშიც მიღებული შედეგი განიხილება, როგორც უსასრულო მცირეთა უსასრულო ჯამი. უსასრულო მცირეთა გამოთვლა არის დიფერენციალური და ინტეგრალური გამოთვლების ზოგადი კონცეფცია, რომელიც საფუძვლად უდევს თანამედროვე უმაღლესი მათემატიკას. უსასრულო სიდიდის ცნება მჭიდროდაა დაკავშირებული ლიმიტის ცნებასთან.

უსასრულოდ მცირე

ფუნქციას ეძახიან უსასრულოდ მცირე წერტილის სიახლოვეს დაურეკა 0 თუ .

ფუნქციას ეძახიან უსასრულოდ მცირე უსასრულობაში, თუ ან .

უსაზღვროდ დიდი რაოდენობით

ყველა ქვემოთ მოცემულ ფორმულაში, უსასრულობა თანასწორობის მარჯვნივ იგულისხმება გარკვეული ნიშნით (ან „პლუს“ ან „მინუს“). ეს არის, მაგალითად, ფუნქცია დაურეკაცოდვა დაურეკა, შეუზღუდავი ორივე მხრიდან, არ არის უსასრულოდ დიდი ზე.

ქვემიმდევრობა ა ნდაურეკა უსასრულოდ დიდი, თუ .

ფუნქციას ეძახიან უსასრულოდ დიდი წერტილის სიახლოვეს დაურეკა 0 თუ .

ფუნქციას ეძახიან უსასრულოდ დიდი უსასრულობაში, თუ ან .

უსასრულოდ მცირე და უსასრულოდ დიდის თვისებები

უსასრულო მცირეთა შედარება

განმარტებები

ასეთი ლიმიტების გამოსათვლელად მოსახერხებელია L'Hopital-ის წესის გამოყენება.

შედარების მაგალითები

გამოყენება შესახებ-სიმბოლიკა, მიღებული შედეგები შეიძლება ჩაიწეროს შემდეგი ფორმით დაურეკა 5 = ო(დაურეკა 3). ამ შემთხვევაში, შემდეგი ჩანაწერები მართალია: 2დაურეკა 2 + 6დაურეკა = ო(დაურეკა) და დაურეკა = ო(2დაურეკა 2 + 6დაურეკა).

ექვივალენტური მნიშვნელობები

განმარტება

როდესაც შემდეგი ეკვივალენტური მიმართებები მოქმედებს (როგორც ე.წ. აღსანიშნავი ლიმიტების შედეგები):

თეორემა

ამ თეორემას აქვს პრაქტიკული მნიშვნელობა ლიმიტების პოვნისას (იხ. მაგალითი).

გამოყენების მაგალითი

ჩანაცვლება სმენ 2დაურეკა ექვივალენტური ღირებულება 2 დაურეკა, ვიღებთ

ისტორიული ჩანახატი

აგრეთვე იხილეთ

ფონდი ვიკიმედია.

ნახეთ, რა არის „უსასრულოდ მცირე რაოდენობა“ სხვა ლექსიკონებში:

უსაზღვროდ მცირე რაოდენობით- ცვლადი სიდიდე გარკვეულ პროცესში, თუ ამ პროცესში ის უსასრულოდ უახლოვდება (მიდრეკილია) ნულამდე... დიდი პოლიტექნიკური ენციკლოპედია

უსასრულოდ მცირე- ■ რაღაც უცნობი, მაგრამ დაკავშირებული ჰომეოპათიასთან... საერთო ჭეშმარიტების ლექსიკა

სექციები