سخنرانی 4.

تداوم توابع

1. تداوم یک تابع در یک نقطه

تعریف 1.اجازه دهید تابع y=f(x) در نقطه تعریف شده است X 0 و در برخی از محله های این نقطه. تابع y=f(x) نامیده می شود پیوسته در نقطه x 0 ، اگر در این نقطه حدی از تابع وجود داشته باشد و با مقدار تابع در این نقطه برابر باشد، i.e.

بنابراین شرط تداوم تابع است y=f(x) در نقطه X 0 این است که:

چون
، سپس برابری (32) را می توان به شکل نوشت

(33)

به این معنی که وقتی یافتن حد یک تابع پیوستهf(x) می توان به حد زیر علامت تابع رفت، یعنی. به یک تابع f(x) به جای استدلال Xمقدار حدی آن را جایگزین کنید X 0 .

لیم گناه x= گناه (lim x);

lim arctg x=arctg(lim x); (34)

lim log x=log(Lim x).

ورزش کنید.حد را پیدا کنید: 1)
; 2)
.

اجازه دهید تداوم یک تابع را بر اساس مفاهیم افزایش آرگومان و تابع تعریف کنیم.

چون شرایط
و
یکسان هستند (شکل 4)، سپس برابری (32) به شکل زیر است:

یا
.

تعریف 2.تابع y=f(x) نامیده می شود پیوسته در نقطه x 0 , اگر در نقطه ای تعریف شده باشد X 0 و همسایگی آن، و یک افزایش بی نهایت کوچک در آرگومان با یک افزایش بی نهایت کوچک در تابع مطابقت دارد.

ورزش کنید.تداوم یک تابع را بررسی کنید y=2X 2 1.

خواص توابع پیوسته در یک نقطه

1. اگر توابع f(x) و φ (x) در نقطه ممتد هستند X 0، سپس مجموع آنها
، کار
و خصوصی
(با توجه به اینکه
) توابع پیوسته در نقطه هستند X 0 .

2. اگر تابع در=f(x) در نقطه ممتد است X 0 و f(x 0)> 0، پس چنین همسایگی نقطه وجود دارد X 0، که در آن f(x)>0.

3. اگر تابع در=f(تو) در نقطه u 0 پیوسته است و تابع u= φ (x) در نقطه ممتد است u 0 = φ (x 0 ) سپس یک تابع پیچیده y=f[φ (x)] در نقطه پیوسته است X 0 .

2. پیوستگی یک تابع در بازه و روی یک قطعه

عملکرد y=f(x) نامیده می شود پیوسته در بازه (الف; ب) اگر در هر نقطه از این بازه پیوسته باشد.

عملکرد y=f(x) نامیده می شود پیوسته در بخش [الف; ب] اگر در بازه ( الف; ب) و در نقطه X=الفدرست استمراری است (یعنی
) و در نقطه x=بپیوسته رها می شود (یعنی
).

3. نقاط ناپیوستگی توابع و طبقه بندی آنها

نقاطی که تداوم یک تابع در آنها شکسته می شود نامیده می شوند نقاط شکستاین تابع.

اگر X=X 0 - نقطه شکست تابع y=f(x) پس حداقل یکی از شرایط تعریف اول تداوم یک تابع برآورده نمی شود.

مثال.

1.
. 2.

3)
4)
.

▼ نقطه شکست X 0 نقطه شکست نامیده می شود اولین نوعتوابع y=f(x، اگر در این نقطه محدودیت های محدودی از تابع در سمت چپ و راست وجود داشته باشد (محدودیت های یک طرفه)، یعنی.
و
. در این مورد:

بزرگی | الف 1 -الف 2 | تماس گرفت عملکرد پرشدر نقطه ناپیوستگی نوع اول. ▲

▼ نقطه شکست X 0 نقطه شکست نامیده می شود نوع دومتوابع y=f(x) در صورتی که حداقل یکی از حدود یک طرفه (چپ یا راست) وجود نداشته باشد یا مساوی بی نهایت باشد. ▲

ورزش کنید.نقاط شکست را پیدا کنید و نوع آنها را برای توابع بیابید:

1)
; 2)
.

4. قضایای اساسی در مورد توابع پیوسته

قضایای تداوم توابع مستقیماً از قضایای مربوط به حدود پیروی می کنند.

قضیه 1.مجموع، حاصلضرب و ضریب دو تابع پیوسته یک تابع پیوسته است (برای ضریب، به جز آن دسته از مقادیر آرگومان که در آن مقسوم علیه برابر با صفر نیست).

قضیه 2.اجازه دهید توابع تو=φ (x) در نقطه ممتد است X 0 و تابع y=f(تو) در نقطه ممتد است تو=φ (x 0 ). سپس تابع مختلط f(φ (x))، متشکل از توابع پیوسته، در نقطه پیوسته است X 0 .

قضیه 3.اگر تابع y=f(x) پیوسته و کاملاً یکنواخت در [ الف; ب] محورها اوه، سپس تابع معکوس در=φ (x) همچنین در بخش مربوطه پیوسته و یکنواخت است [ ج;د] محورها اوه

هر عملکرد ابتداییپیوسته در هر نقطه ای که در آن تعریف می شود.

5. خواص توابع پیوسته در یک بازه

قضیه وایرشتراس.اگر تابعی روی یک قطعه پیوسته باشد، به حداکثر و حداقل مقدار خود در این بخش می رسد.

نتیجه.اگر تابعی در یک بازه پیوسته باشد، در آن بازه محدود می شود.

قضیه بولزانو کوشی.اگر تابع y=f(x) در بازه [ الف; ب] و در انتهای خود مقادیر نابرابر می گیرد f(الف)=الفو f(ب)=ب,
، سپس هر عددی که باشد با، بین الفو در،یک نکته وجود دارد
به گونه ای که f(ج)=سی.

از نظر هندسیقضیه بدیهی است برای هر تعداد با، بین الفو در، یک نقطه c در داخل این قطعه وجود دارد به طوری که f(با)=سی. مستقیم در=بانمودار تابع را حداقل در یک نقطه قطع می کند.

نتیجه.اگر تابع y=f(x) در بازه [ الف; ب] و مقادیر نشانه های مختلف را در انتهای خود به خود می گیرد، سپس در داخل قطعه [ الف; ب] حداقل یک نکته وجود دارد با، که در آن تابع y=f(x) به صفر می رسد: f(ج)=0.

هندسیمعنی قضیه: اگر نمودار یک تابع پیوسته از یک سمت محور عبور کند اوهبه دیگری، سپس محور را قطع می کند اوه.

تداوم یک تابع در یک نقطه

اجازه دهید تابع f(x) در همسایگی O(x0) نقطه x0 (شامل خود نقطه x0) تعریف شود.

تابع f(x) در نقطه x0 پیوسته نامیده می شود اگر limx → x0 f(x) برابر با مقدار تابع f(x) در این نقطه وجود داشته باشد: lim

f(x) = f(x0)، (1)

آن ها "O(f(x0)) $ O(x0) : x O O(x0) Yu f(x) O O(f(x0)) .

نظر دهید. تساوی (1) را می توان به صورت زیر نوشت: lim

آن ها تحت علامت یک تابع پیوسته می توان به حد حد رسید.

فرض کنید Δx = x - x0 افزایش آرگومان باشد، Δy = f(x) - f(x0) افزایش متناظر تابع باشد.

لازم و شرایط کافیتداوم یک تابع در یک نقطه

تابع y = f(x) در x0 پیوسته است اگر و فقط اگر

نظر دهید. شرط (2) را می توان به عنوان دومین تعریف از پیوستگی یک تابع در یک نقطه تفسیر کرد. هر دو تعریف معادل هستند.

اجازه دهید تابع f(x) در نیم بازه تعریف شود.

به تابع f(x) گفته می شود که اگر حد یک طرفه وجود داشته باشد در x0 پیوسته باقی می ماند

پیوستگی حاصل جمع، حاصلضرب و ضریب دو تابع پیوسته

قضیه 1. اگر توابع f(x) و g(x) در نقطه x0 پیوسته باشند، آنگاه f(x) ± g(x)، f(x) g(x)، f(x) در این نقطه پیوسته هستند. نقطه

تداوم یک تابع پیچیده

قضیه 2. اگر تابع u(x) در نقطه x0 پیوسته باشد و تابع f(u) در نقطه متناظر u0 = f(x0) پیوسته باشد، تابع مختلط f(u(x)) پیوسته است. در نقطه x0.

همه توابع ابتدایی در هر نقطه از حوزه تعریف خود پیوسته هستند.

خواص محلی توابع پیوسته

قضیه 3 (محدوده تابع پیوسته).

اگر تابع f(x) در x0 پیوسته باشد، یک همسایگی O(x0) وجود دارد که در آن f(x) محدود است.

اثبات از عبارتی در مورد کران بودن تابعی که دارای حد است به دست می آید.

قضیه 4 (پایداری علامت تابع پیوسته).

اگر تابع f(x) در نقطه x0 و f(x0) ≠ 0 پیوسته باشد، همسایگی نقطه x0 وجود دارد که در آن f(x) ≠ 0، و علامت f(x) در این همسایگی وجود دارد. با علامت f(x0) منطبق است.

طبقه بندی نقاط شکست

شرط (1) برای پیوستگی تابع f(x) در نقطه x0 معادل شرط f(x0 − 0) = f(x0 + 0) = f(x0)، (3) است.

که در آن f(x 0 − 0) = lim

f(x) و f(x0 + 0) = lim

f(x) - حدود یک طرفه تابع f(x) در نقطه x0.

اگر شرط (3) نقض شود، نقطه x0 را نقطه ناپیوستگی تابع f(x) می نامند. بسته به نوع نقض شرط (3)، نقاط شکست ماهیت متفاوتی دارند و به شرح زیر طبقه بندی می شوند:

1. اگر در نقطه x0 حدهای یک طرفه f(x0 − 0)، f (x0 + 0) و

f(x0 − 0) = f(x0 + 0) ≠ f(x0)، سپس نقطه x0 را نقطه ناپیوستگی قابل جابجایی تابع f(x) می نامند (شکل 1).

نظر دهید. در نقطه x0 ممکن است تابع تعریف نشده باشد.

2. اگر در نقطه x0 حدهای یک طرفه f(x0 − 0)، f (x0 + 0) و

f(x0 − 0) ≠ f(x0 + 0)، سپس نقطه x0 یک نقطه ناپیوستگی با یک پرش متناهی تابع f(x) نامیده می شود (شکل 2). نظر دهید. در نقطه ناپیوستگی با یک پرش محدود، مقدار تابع می تواند هر کدام باشد یا ممکن است تعریف نشود.نقاط ناپیوستگی قابل جابجایی و پرش محدود را نقاط ناپیوستگی نوع 1 می نامند. آنها

3. اگر در نقطه x0 حداقل یکی از حدهای یک طرفه f(x0 − 0)، f (x0 + 0) برابر بی نهایت باشد یا وجود نداشته باشد،
x0 یک نقطه ناپیوستگی از نوع دوم نامیده می شود (شکل 3).

اگر حداقل یکی از حدهای یک طرفه f(x0 − 0)، f (x0 + 0) برابر بی نهایت باشد، خط مستقیم x = x 0 مجانب عمودی نمودار تابع y = f نامیده می شود. (x).

تعریف. تابع f(x)، که در همسایگی نقطه x0 تعریف شده است، در نقطه x0 پیوسته نامیده می شود اگر حد تابع و مقدار آن در این نقطه برابر باشد، یعنی.

همین واقعیت را می توان متفاوت نوشت:

تعریف. اگر تابع f(x) در محله ای از نقطه x0 تعریف شده باشد، اما در خود نقطه x0 پیوسته نباشد، آن را تابع ناپیوسته و نقطه x0 را نقطه ناپیوستگی می نامند.

تعریف. تابع f(x) در نقطه x0 در صورت وجود پیوسته گفته می شود عدد مثبت e>0 عدد D>0 وجود دارد به طوری که برای هر x که شرط را برآورده می کند

نابرابری درست است

تعریف.

تابع f(x) در نقطه x = x0 پیوسته نامیده می شود اگر افزایش تابع در نقطه x0 یک مقدار بی نهایت کوچک باشد.

f(x) = f(x0) + a(x)

که در آن a(x) در x®x0 بی نهایت کوچک است.

خواص توابع پیوسته

1) مجموع، تفاوت و حاصلضرب توابع پیوسته در نقطه x0 تابعی است پیوسته در نقطه x0. 2) ضریب دو تابع پیوسته استعملکرد پیوسته

مشروط بر اینکه g(x) در نقطه x0 برابر با صفر نباشد.

3) برهم نهی توابع پیوسته یک تابع پیوسته است.

این ویژگی را می توان به صورت زیر نوشت:

اگر u = f(x)، v = g(x) توابع پیوسته در نقطه x = x0 باشند، تابع v = g(f(x)) نیز در این نقطه یک تابع پیوسته است.

با استفاده از قضایای حدی می توان صحت ویژگی های فوق را به راحتی اثبات کرد

خواص توابع پیوسته در یک بازه.

خاصیت 1: (اولین قضیه وایرشتراس (وایرشتراس کارل (1815-1897) - ریاضیدان آلمانی)). تابعی که در یک بازه پیوسته است در این بازه محدود می شود، یعنی. شرط –M £ f(x) £ M در بخش ارضا می شود.

اثبات این خاصیت مبتنی بر این واقعیت است که تابعی که در نقطه x0 پیوسته است در همسایگی خاصی از آن محدود شده است و اگر قطعه را به تعداد نامتناهی قطعه تقسیم کنید که به نقطه x0 «انقباض» شده اند. ، سپس یک همسایگی مشخص از نقطه x0 تشکیل می شود.

خاصیت 2: تابعی که در یک بازه پیوسته است بزرگترین و کوچکترین مقدار خود را می گیرد.

آن ها مقادیر x1 و x2 وجود دارد به طوری که f(x1) = m، f(x2) = M، و

تفاوت بین بزرگترین و کوچکترین مقدار یک تابع در بازه را نوسان تابع در یک بازه می گویند.

خاصیت 3: (قضیه دوم بولزانو-کوشی). تابعی که در بازه پیوسته است، تمام مقادیر بین دو مقدار دلخواه را در این بازه می گیرد.

خاصیت 4: اگر تابع f(x) در نقطه x = x0 پیوسته باشد، آنگاه مقداری همسایگی نقطه x0 وجود دارد که در آن تابع علامت خود را حفظ می کند.

خاصیت 5: (قضیه اول بولزانو (1781-1848) – کوشی). اگر یک تابع f(x) روی یک قطعه پیوسته باشد و دارای مقادیری از علائم متضاد در انتهای قطعه باشد، آنگاه نقطه ای در داخل این قطعه وجود دارد که f(x) = 0 است.

آن ها اگر علامت(f(a)) 1 علامت(f(b))، سپس x0 $: f(x0) = 0.

تعریف. یک تابع f(x) به طور یکنواخت در بازه زمانی گفته می شود که برای هر e> 0 D> 0 وجود داشته باشد به طوری که برای هر نقطه x1O و x2O به طوری که

ïx2 – x1ï< D

نابرابری ïf(x2) – f(x1)ï درست است< e

تفاوت بین پیوستگی یکنواخت و پیوستگی "معمولی" در این است که برای هر e D خود مستقل از x وجود دارد و با تداوم "معمولی" D به e و x بستگی دارد.

ویژگی 6: قضیه کانتور (Georg Cantor (1845-1918) - ریاضیدان آلمانی). تابع پیوسته روی یک قطعه به طور یکنواخت بر روی آن پیوسته است.

(این ویژگی فقط برای بخش ها صادق است و نه برای فواصل و نیمه بازه ها.)

تعریف تداوم

تابع f (x) در نقطه a پیوسته نامیده می شود اگر: f () pp

1) تابع f(x) در نقطه a تعریف شده است،

2) دارای یک حد محدود به عنوان x → a 2) دارای یک حد محدود به عنوان x → a،

3) این حد برابر است با مقدار تابع در این نقطه:

تداوم در بازه

اگر f () pp ru به تابع f (x) در بازه X پیوسته گفته می شود

در هر نقطه از این بازه پیوسته است.

بیانیه همه توابع ابتدایی پیوسته هستند

حوزه های تعریف آنها.

تابع محدود

به یک تابع گفته می شود که در یک بازه if محدود شده است

یک عدد M وجود دارد به طوری که برای تمام x ∈

نابرابری:| f(x)| ≤ م.

دو قضیه وایرشتراس

قضیه اول وایرشتراس. اگر تابع f (x r r r r f f (

بر روی قطعه پیوسته است، سپس بر روی این قطعه محدود می شود

قضیه دوم وایرشتراس.اگر تابع f(x

روی قطعه ممتد است، سپس به این قطعه می رسد

کوچکترین مقدار m و بزرگترین مقدار M.

قضیه بولزانو کوشی

اگر تابع f (x) در قسمت مقدار در f f () pp p پیوسته باشد

در انتهای این بخش f(a) و f(b) دارای علائم متضاد هستند،

در داخل قطعه یک نقطه c∈ (a,b) وجود دارد به طوری که f (c) = 0. ur p () f ()

تداوم عملکرد. نقاط شکست.

گاو نر راه می رود، تاب می خورد، آه می کشد:
- اوه، تخته داره تموم میشه، الان دارم می افتم!

در این درس به بررسی مفهوم پیوستگی یک تابع، طبقه بندی نقاط ناپیوستگی و مشترک می پردازیم. مشکل عملی مطالعات تداوم توابع. از همان نام موضوع، بسیاری به طور مستقیم آنچه را که مورد بحث قرار می گیرد حدس می زنند و فکر می کنند که مطالب بسیار ساده است. این درست است. اما این کارهای ساده هستند که اغلب به دلیل غفلت و رویکرد سطحی برای حل آنها مجازات می شوند. بنابراین، توصیه می کنم مقاله را با دقت مطالعه کنید و تمام ظرافت ها و تکنیک ها را در نظر بگیرید.

چه چیزی را باید بدانید و بتوانید انجام دهید؟نه خیلی زیاد. برای اینکه درس را خوب یاد بگیرید، باید بفهمید که چیست حد یک تابع . برای خوانندگانی که سطح آمادگی پایینی دارند، درک مطلب کافی است محدودیت های عملکرد نمونه هایی از راه حل ها و ببینید معنی هندسیمحدودیت در دفترچه راهنما نمودارها و خواص توابع ابتدایی . همچنین توصیه می شود با آن آشنا شوید تبدیل هندسی نمودارها ، از آنجایی که تمرین در بیشتر موارد شامل ساخت یک نقاشی است. چشم انداز برای همه خوش بین است، و حتی یک کتری پر می تواند در یکی دو ساعت آینده به تنهایی با این کار کنار بیاید!

تداوم عملکرد. نقاط شکست و طبقه بندی آنها

مفهوم تداوم عملکرد

بیایید تابعی را در نظر بگیریم که در کل خط اعداد پیوسته است:

یا به بیان مختصرتر، تابع ما پیوسته است (مجموعه اعداد حقیقی).

ملاک تداوم «فلسطه» چیست؟ بدیهی است که نمودار یک تابع پیوسته را می توان بدون برداشتن مداد از روی کاغذ رسم کرد.

در این مورد، دو مفهوم ساده باید به وضوح متمایز شوند: دامنه یک تابع و تداوم عملکرد. به طور کلی این یک چیز نیست. به عنوان مثال:

این تابعدر کل خط اعداد تعریف شده است، یعنی برای همهمعنی "x" معنای خاص خود را از "y" دارد. به طور خاص، اگر، پس. توجه داشته باشید که نقطه دیگر نقطه گذاری است، زیرا با تعریف یک تابع، مقدار آرگومان باید با تنها چیزمقدار تابع بنابراین، حوزه تعریف عملکرد ما: .

با این حال این تابع پیوسته روشن نیست!کاملاً واضح است که او در آن نقطه رنج می برد شکاف. این اصطلاح در واقع کاملاً قابل درک و بصری است، در اینجا مداد باید از روی کاغذ پاره شود. کمی بعد به طبقه بندی نقاط شکست خواهیم پرداخت.

تداوم یک تابع در یک نقطه و در یک بازه

به این یا آن صورت مسئله ریاضیما می توانیم در مورد تداوم یک تابع در یک نقطه، تداوم یک تابع در یک بازه، یک نیمه بازه، یا تداوم یک تابع در یک قطعه صحبت کنیم. یعنی "تداوم صرف" وجود ندارد- تابع می تواند در جایی پیوسته باشد. و "ساختمان" اساسی هر چیز دیگری است تداوم عملکرد در نقطه .

نظریه تجزیه و تحلیل ریاضیتعریفی از تداوم یک تابع در یک نقطه با استفاده از همسایگی های "دلتا" و "اپسیلون" ارائه می دهد، اما در عمل تعریف دیگری در حال استفاده وجود دارد که ما به آن توجه زیادی خواهیم کرد.

اول یادمون باشه محدودیت های یک طرفهکه در اولین درس وارد زندگی ما شدند در مورد نمودارهای تابع . یک موقعیت روزمره را در نظر بگیرید:

اگر محور را به نقطه نزدیک کنیم سمت چپ(فلش قرمز)، سپس مقادیر مربوط به "بازی ها" در امتداد محور به نقطه (فلش زرشکی) می روند. از نظر ریاضی، این واقعیت با استفاده از آن ثابت می شود حد چپ:

به ورودی توجه کنید (خوانده می شود "x تمایل به ka در سمت چپ"). "افزودنی" "منهای صفر" نماد است ، در اصل این بدان معنی است که ما از سمت چپ به عدد نزدیک می شویم.

به همین ترتیب، اگر به نقطه "ka" نزدیک شوید درست است(فلش آبی)، سپس "بازی ها" به همان مقدار می رسند، اما در امتداد فلش سبز، و حد سمت راستبه صورت زیر فرمت خواهد شد:

"افزودنی" نماد است و مدخل می‌خواند: "x در سمت راست به ka تمایل دارد."

اگر حدود یک طرفه محدود و مساوی باشد(مانند مورد ما): ، سپس خواهیم گفت که یک حد کلی وجود دارد. ساده است، محدودیت کلی "معمول" ما است حد یک تابع ، برابر با یک عدد متناهی است.

توجه داشته باشید که اگر تابع در (نقطه سیاه در شاخه نمودار) تعریف نشده باشد، محاسبات بالا معتبر می مانند. همانطور که قبلاً چندین بار به ویژه در مقاله ذکر شده است در توابع بی نهایت کوچک ، عبارات به این معنی است که "x" بی نهایت نزدیکبه نقطه نزدیک می شود، در حالی که مهم نیست، آیا خود تابع در یک نقطه مشخص تعریف شده است یا خیر. مثال خوبدر پاراگراف بعدی، زمانی که تابع تجزیه و تحلیل می شود، ظاهر می شود.

تعریف: یک تابع در یک نقطه پیوسته است اگر حد تابع در یک نقطه معین برابر با مقدار تابع در آن نقطه باشد: .

این تعریف به شرح زیر است:

1) تابع باید در نقطه تعریف شود، یعنی مقدار باید وجود داشته باشد.

2) باید یک محدودیت کلی برای تابع وجود داشته باشد. همانطور که در بالا ذکر شد، این دلالت بر وجود و برابری حدود یک طرفه دارد: .

3) حد تابع در یک نقطه معین باید برابر با مقدار تابع در این نقطه باشد: .

اگر نقض شود حداقل یکیاز سه شرط، سپس تابع خاصیت پیوستگی را در نقطه از دست می دهد.

تداوم یک تابع در یک بازه زمانیمبتکرانه و بسیار ساده فرموله شده است: یک تابع در بازه زمانی پیوسته است که در هر نقطه از بازه داده شده پیوسته باشد.

به طور خاص، بسیاری از توابع در یک بازه نامتناهی، یعنی روی مجموعه اعداد حقیقی، پیوسته هستند. این یک تابع خطی، چند جمله ای، نمایی، سینوس، کسینوس و غیره است. و به طور کلی، هر عملکرد ابتدایی مداوم بر روی آن حوزه تعریف برای مثال، یک تابع لگاریتمی بر روی بازه پیوسته است. امیدوارم در این لحظهشما ایده بسیار خوبی از شکل نمودارهای توابع اصلی دارید. بیشتر اطلاعات دقیقتداوم آنها را می توان از آنها استخراج کرد فرد مهربانبا نام خانوادگی Fichtengolts.

با تداوم یک تابع در یک بخش و نیم فواصل، همه چیز نیز دشوار نیست، اما بهتر است در این مورد در کلاس صحبت کنیم. در مورد یافتن حداقل و حداکثر مقادیر یک تابع در یک قطعه ، اما فعلاً نگران آن نباشیم.

طبقه بندی نقاط شکست

زندگی جذاب توابع سرشار از انواع نقاط خاص است و نقاط شکست تنها یکی از صفحات بیوگرافی آنهاست.

توجه داشته باشید : در هر صورت، من روی یک نکته ابتدایی می مانم: نقطه شکست همیشه است نقطه واحد- هیچ "چند نقطه شکست در یک ردیف" وجود ندارد، یعنی چیزی به نام "فاصله استراحت" وجود ندارد.

این نقاط به نوبه خود به دو گروه بزرگ تقسیم می شوند: پارگی های نوع اولو پارگی های نوع دوم. هر نوع شکاف مختص به خود را دارد ویژگی های مشخصهکه اکنون به آن خواهیم پرداخت:

نقطه ناپیوستگی از نوع اول

اگر شرط تداوم در نقطه ای نقض شود و محدودیت های یک طرفه متناهی ، سپس نامیده می شود نقطه ناپیوستگی از نوع اول.

بیایید با خوش بینانه ترین مورد شروع کنیم. با توجه به ایده اصلی درس، می خواستم این نظریه را بگویم «در نمای کلی"، اما برای نشان دادن واقعیت مطالب، روی گزینه ای با شخصیت های خاص استقرار کردم.

این غم انگیز است، مانند عکسی از تازه ازدواج کرده ها در پس زمینه شعله ابدی، اما عکس زیر به طور کلی پذیرفته شده است. اجازه دهید نمودار تابع را در نقاشی به تصویر بکشیم:


این تابع در تمام خط اعداد به جز نقطه پیوسته است. و در واقع مخرج نمی تواند برابر با صفر باشد. با این حال، مطابق با معنای حد، می توانیم بی نهایت نزدیکهم از سمت چپ و هم از راست به "صفر" نزدیک شوید، یعنی محدودیت های یک طرفه وجود دارد و بدیهی است که منطبق هستند:
(شرط شماره 2 تداوم برقرار است).

اما تابع در نقطه تعریف نشده است، بنابراین، شرط شماره 1 تداوم نقض می شود و تابع در این نقطه دچار ناپیوستگی می شود.

گسست از این نوع (با موجود حد کلی) نامیده می شوند شکاف قابل تعمیر. چرا قابل جابجایی؟ زیرا تابع می تواند دوباره تعریف کنددر نقطه شکست:

عجیب به نظر می رسد؟ شاید. اما چنین نشانه گذاری تابعی با هیچ چیز تناقض ندارد! حالا این شکاف بسته شده و همه خوشحال هستند:


بیایید یک بررسی رسمی انجام دهیم:

2) - یک محدودیت کلی وجود دارد.
3)

بنابراین، هر سه شرط برآورده می شوند و تابع در یک نقطه با تعریف تداوم یک تابع در یک نقطه، پیوسته است.

با این حال، متنفران از ماتان می توانند عملکرد را به عنوان مثال بد تعریف کنند :


جالب است که دو شرط تداوم اول در اینجا برآورده می شوند:
1) - تابع در یک نقطه مشخص تعریف شده است.
2) - یک محدودیت کلی وجود دارد.

اما از مرز سوم عبور نکرده است: یعنی حد تابع در نقطه برابر نیستمقدار یک تابع معین در یک نقطه معین

بنابراین، در یک نقطه تابع دچار ناپیوستگی می شود.

مورد دوم غم انگیزتر نامیده می شود پارگی از نوع اول با یک پرش. و اندوه با محدودیت های یک طرفه برانگیخته می شود متناهی و متفاوت. یک مثال در نقاشی دوم درس نشان داده شده است. چنین شکافی معمولاً در توابع تعریف شده تکه ای، که قبلاً در مقاله ذکر شده است در مورد تبدیل نمودار .

تابع تکه ای را در نظر بگیرید و رسم آن را کامل می کنیم. چگونه یک نمودار بسازیم؟ خیلی ساده در یک نیم فاصله، قطعه ای از سهمی را رسم می کنیم ( سبز، در فاصله - یک پاره خط مستقیم (قرمز) و در یک نیمه فاصله - یک خط مستقیم (آبی).

علاوه بر این، به دلیل نابرابری، مقدار برای تابع درجه دوم (نقطه سبز) و به دلیل نابرابری، مقدار برای تابع خطی (نقطه آبی) تعیین می شود.

در سخت‌ترین حالت، باید به ساختن نقطه به نقطه هر قطعه از نمودار متوسل شوید (اول را ببینید درس در مورد نمودار توابع ).

اکنون ما فقط به نکته علاقه مند خواهیم بود. بیایید آن را برای تداوم بررسی کنیم:

2) بیایید حدود یک طرفه را محاسبه کنیم.

در سمت چپ یک بخش خط قرمز داریم، بنابراین حد سمت چپ این است:

در سمت راست خط مستقیم آبی و حد سمت راست است:

در نتیجه دریافت کردیم اعداد متناهی، و آنها برابر نیست. از آنجایی که محدودیت های یک طرفه متناهی و متفاوت: ، سپس عملکرد ما تحمل می کند ناپیوستگی نوع اول با پرش.

منطقی است که شکاف را نمی توان حذف کرد - عملکرد را واقعاً نمی توان بیشتر تعریف کرد و مانند مثال قبلی "به هم چسباند".

نقاط ناپیوستگی نوع دوم

معمولاً تمام موارد دیگر پارگی با هوشمندی در این دسته طبقه بندی می شوند. من همه چیز را فهرست نمی کنم، زیرا در عمل، در 99٪ از مشکلات با شما روبرو خواهید شد شکاف بی پایان- وقتی چپ دست یا راست دست است، و اغلب، هر دو حد نامحدود است.

و البته واضح ترین تصویر هذلولی در نقطه صفر است. در اینجا هر دو حد یک طرفه بی نهایت هستند: بنابراین، تابع در نقطه از نوع دوم دچار ناپیوستگی می شود.

من سعی می کنم مقالات خود را با محتوای متنوع تا حد امکان پر کنم، بنابراین بیایید به نمودار تابعی که هنوز با آن برخورد نشده است نگاه کنیم:

طبق طرح استاندارد:

1) تابع در این مرحله تعریف نشده است زیرا مخرج به صفر می رسد.

البته، بلافاصله می‌توانیم نتیجه بگیریم که تابع در نقطه‌ای دچار ناپیوستگی می‌شود، اما خوب است ماهیت ناپیوستگی را طبقه‌بندی کنیم، که اغلب توسط شرط مورد نیاز است. برای انجام این کار:

یادآوری کنم که منظور ما از ضبط است عدد منفی بینهایت کوچکو زیر مدخل - عدد مثبت بینهایت کوچک.

محدودیت های یک طرفه بی نهایت هستند، به این معنی که تابع از نوع دوم در نقطه ناپیوستگی رنج می برد. محور y است مجانب عمودی برای نمودار

وجود هر دو حد یک طرفه غیر معمول نیست، اما فقط یکی از آنها نامحدود است، برای مثال:

این نمودار تابع است.

نقطه را برای تداوم بررسی می کنیم:

1) تابع در این مرحله تعریف نشده است.

2) بیایید حدود یک طرفه را محاسبه کنیم: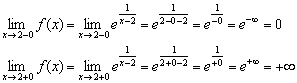

ما در مورد روش محاسبه چنین محدودیت های یک طرفه در دو نمونه آخر سخنرانی صحبت خواهیم کرد، اگرچه بسیاری از خوانندگان قبلاً همه چیز را دیده و حدس زده اند.

حد سمت چپ محدود و برابر با صفر است (ما "به خود نقطه نمی رویم")، اما حد سمت راست بی نهایت است و شاخه نارنجی نمودار بی نهایت به آن نزدیک می شود. مجانب عمودی ، با معادله (خط نقطه سیاه) به دست می آید.

بنابراین عملکرد آسیب می بیند ناپیوستگی نوع دومدر نقطه .

در مورد ناپیوستگی نوع اول، تابع را می توان در خود نقطه ناپیوستگی تعریف کرد. به عنوان مثال، برای یک تابع تکه ای با خیال راحت یک نقطه پررنگ سیاه در مبدأ مختصات قرار دهید. در سمت راست شاخه ای از هذلولی است و حد سمت راست بی نهایت است. من فکر می‌کنم تقریباً همه تصوری از ظاهر این نمودار دارند.

چیزی که همه منتظرش بودند:

چگونه یک تابع را برای تداوم بررسی کنیم؟

مطالعه یک تابع برای تداوم در یک نقطه طبق یک طرح روتین از قبل ایجاد شده انجام می شود که شامل بررسی سه شرط تداوم است:

مثال 1

تابع کاوش

راه حل:

1) تنها نقطه در محدوده جایی است که تابع تعریف نشده است.

2) بیایید حدود یک طرفه را محاسبه کنیم:

حدود یک طرفه متناهی و مساوی هستند.

بنابراین، در نقطه ای که تابع دچار یک ناپیوستگی قابل جابجایی می شود.

نمودار این تابع چگونه است؟

من می خواهم ساده کنم ، و به نظر می رسد که یک سهمی معمولی به دست آمده است. اماتابع اصلی در نقطه تعریف نشده است، بنابراین عبارت زیر مورد نیاز است:

بیایید نقاشی را انجام دهیم:

پاسخ دهید: تابع در تمام خط اعداد پیوسته است به جز نقطه ای که در آن یک ناپیوستگی قابل جابجایی متحمل می شود.

تابع را می توان به روشی خوب یا نه چندان خوب تعریف کرد، اما با توجه به شرایط این کار لازم نیست.

شما می گویید این یک مثال دور از ذهن است؟ نه اصلا. در عمل ده ها بار این اتفاق افتاده است. تقریباً تمام وظایف سایت از کار و آزمایش مستقل واقعی است.

بیایید از شر ماژول های مورد علاقه خود خلاص شویم:

مثال 2

تابع کاوش برای تداوم در صورت وجود، ماهیت ناپیوستگی های تابع را تعیین کنید. طراحی را اجرا کنید.

راه حل: به دلایلی، دانش آموزان می ترسند و عملکردهای ماژول را دوست ندارند، اگرچه هیچ چیز پیچیده ای در مورد آنها وجود ندارد. قبلاً در درس کمی به چنین مواردی پرداخته ایم. تبدیل هندسی نمودارها . از آنجایی که ماژول غیر منفی است، به صورت زیر گسترش می یابد: ، که در آن "آلفا" برخی از عبارت ها است. در در این مورد، و تابع ما باید به صورت تکه ای نوشته شود:

اما کسرهای هر دو قطعه باید کاهش یابد. کاهش، مانند مثال قبلی، بدون عواقب انجام نخواهد شد. تابع اصلی در نقطه تعریف نمی شود زیرا مخرج به صفر می رسد. بنابراین، سیستم باید علاوه بر این شرط را مشخص کند و اولین نابرابری را سخت کند:

اکنون در مورد یک تکنیک تصمیم گیری بسیار مفید: قبل از نهایی کردن کار روی یک پیش نویس، انجام یک نقاشی (صرف نظر از اینکه شرایط لازم باشد یا خیر) مفید است. این کمک می کند که اولاً فوراً نقاط تداوم و نقاط ناپیوستگی را مشاهده کنید و ثانیاً هنگام یافتن محدودیت های یک طرفه 100٪ از شما در برابر خطا محافظت می کند.

بیایید نقاشی را انجام دهیم. مطابق با محاسبات ما، در سمت چپ نقطه لازم است قطعه ای از سهمی (رنگ آبی) و در سمت راست - یک قطعه سهمی (رنگ قرمز) ترسیم شود، در حالی که تابع در قسمت مشخص نشده است. خود نقطه:

اگر شک دارید، چند مقدار x بگیرید و آنها را به تابع وصل کنید (به یاد داشته باشید که ماژول علامت منفی احتمالی را از بین می برد) و نمودار را بررسی کنید.

اجازه دهید تابع پیوستگی را به صورت تحلیلی بررسی کنیم:

1) تابع در نقطه تعریف نشده است، بنابراین می توانیم بلافاصله بگوییم که در آن پیوسته نیست.

2) بیایید ماهیت ناپیوستگی را مشخص کنیم، برای انجام این کار، محدودیت های یک طرفه را محاسبه می کنیم.

حدود یک طرفه محدود و متفاوت هستند، به این معنی که تابع با یک پرش در نقطه دچار ناپیوستگی از نوع اول می شود. مجدداً توجه داشته باشید که هنگام یافتن محدودیت ها، فرقی نمی کند که تابع در نقطه شکست تعریف شده باشد یا خیر.

اکنون تنها چیزی که باقی می ماند این است که نقاشی را از پیش نویس منتقل کنید (انگار با کمک تحقیق ساخته شده است ;-)) و کار را کامل کنید:

پاسخ دهید: تابع در تمام خط اعداد پیوسته است به جز نقطه ای که با یک پرش دچار ناپیوستگی از نوع اول می شود.

گاهی اوقات آنها نیاز به نشانه اضافی از پرش ناپیوستگی دارند. به سادگی محاسبه می شود - از حد سمت راست باید حد چپ را کم کنید: ، یعنی در نقطه شکست تابع ما 2 واحد به پایین پرید (همانطور که علامت منفی به ما می گوید).

مثال 3

تابع کاوش برای تداوم در صورت وجود، ماهیت ناپیوستگی های تابع را تعیین کنید. یک نقاشی بکشید.

این یک مثال برای تصمیم مستقل، نمونه راه حل در پایان درس.

بیایید به محبوب ترین و گسترده ترین نسخه کار برویم، زمانی که تابع از سه بخش تشکیل شده است:

مثال 4

یک تابع را از نظر تداوم بررسی کنید و نمودار آن را رسم کنید .

راه حل: بدیهی است که هر سه قسمت تابع در فواصل مربوطه پیوسته هستند، بنابراین فقط باید دو نقطه "اتصال" بین قطعات بررسی شود. ابتدا بیایید یک پیش نویس طراحی کنیم. تنها نکته این است که ما باید نکات منحصر به فرد خود را به دقت دنبال کنیم: به دلیل نابرابری، مقدار به خط مستقیم (نقطه سبز) و به دلیل نابرابری، مقدار متعلق به سهمی (نقطه قرمز) است.


خوب، در اصل، همه چیز روشن است =) تنها چیزی که باقی می ماند رسمی کردن تصمیم است. برای هر یک از دو نقطه "اتصال"، ما به طور استاندارد 3 شرط تداوم را بررسی می کنیم:

من)نقطه را برای تداوم بررسی می کنیم

1)

حدود یک طرفه محدود و متفاوت هستند، به این معنی که تابع با یک پرش در نقطه دچار ناپیوستگی از نوع اول می شود.

اجازه دهید پرش ناپیوستگی را به عنوان تفاوت بین حد راست و چپ محاسبه کنیم:
، یعنی نمودار یک واحد به سمت بالا حرکت کرد.

II)نقطه را برای تداوم بررسی می کنیم

1) - تابع در یک نقطه مشخص تعریف شده است.

2) محدودیت های یک طرفه را پیدا کنید:

- حدود یک طرفه متناهی و مساوی هستند، یعنی یک حد کلی وجود دارد.

3) - حد یک تابع در یک نقطه برابر است با مقدار این تابع در یک نقطه مشخص.

در مرحله نهایی، نقاشی را به نسخه نهایی منتقل می کنیم و پس از آن آکورد نهایی را قرار می دهیم:

پاسخ دهید: تابع در امتداد تمام خط اعداد پیوسته است، به جز نقطه ای که در آن یک ناپیوستگی از نوع اول با یک پرش را تجربه می کند.

مثال 5

یک تابع را از نظر تداوم بررسی کنید و نمودار آن را بسازید .

این یک مثال برای حل مستقل، یک راه حل کوتاه و یک نمونه تقریبی از مسئله در پایان درس است.

ممکن است این تصور را داشته باشید که در یک نقطه تابع باید پیوسته باشد و در نقطه دیگر باید ناپیوستگی وجود داشته باشد. در عمل، همیشه اینطور نیست. سعی کنید از نمونه های باقی مانده غافل نشوید - چندین ویژگی جالب و مهم وجود خواهد داشت:

مثال 6

یک تابع داده شده است . تابع تداوم در نقاط را بررسی کنید. یک نمودار بسازید.

راه حل: و دوباره بلافاصله نقشه را روی پیش نویس اجرا کنید:

ویژگی این نمودار این است که تابع تکه ای با معادله محور آبسیسا داده می شود. این منطقه در اینجا ترسیم شده است سبز، و در یک دفترچه معمولاً با پررنگ مشخص می شود با یک مداد ساده. و البته، قوچ های ما را فراموش نکنید: مقدار به شاخه مماس (نقطه قرمز) و مقدار متعلق به خط مستقیم است.

همه چیز از نقاشی مشخص است - تابع در طول کل خط اعداد پیوسته است، تنها چیزی که باقی می ماند رسمی کردن راه حل است که به معنای واقعی کلمه پس از 3-4 مثال مشابه به اتوماسیون کامل می رسد:

من)نقطه را برای تداوم بررسی می کنیم

1) - تابع در یک نقطه مشخص تعریف شده است.

2) بیایید حدود یک طرفه را محاسبه کنیم:

یعنی محدودیت کلی وجود دارد.

در هر صورت، اجازه دهید یک واقعیت بی اهمیت را به شما یادآوری کنم: حد یک ثابت برابر با خود ثابت است. در این صورت حد صفر برابر است با خود صفر (حد چپ).

3) - حد یک تابع در یک نقطه برابر است با مقدار این تابع در یک نقطه مشخص.

بنابراین، یک تابع در یک نقطه با تعریف تداوم یک تابع در یک نقطه پیوسته است.

II)نقطه را برای تداوم بررسی می کنیم

1) - تابع در یک نقطه مشخص تعریف شده است.

2) محدودیت های یک طرفه را پیدا کنید:

و در اینجا - حد یک برابر با خود واحد است.

- یک محدودیت کلی وجود دارد.

3) - حد یک تابع در یک نقطه برابر است با مقدار این تابع در یک نقطه مشخص.

بنابراین، یک تابع در یک نقطه با تعریف تداوم یک تابع در یک نقطه پیوسته است.

طبق معمول، پس از تحقیق، نقاشی خود را به نسخه نهایی منتقل می کنیم.

پاسخ دهید: تابع در نقاط پیوسته است.

لطفاً توجه داشته باشید که در شرایط از ما چیزی در مورد مطالعه کل تابع برای تداوم سؤال نشده است و فرمول بندی آن فرم ریاضی خوبی در نظر گرفته می شود. دقیق و واضحپاسخ به سوال مطرح شده ضمناً اگر شرایط ایجاب نمی کند که گراف بسازید، پس حق دارید که آن را نسازید (البته بعداً معلم می تواند شما را مجبور به انجام این کار کند).

یک "پیچان زبان" کوچک ریاضی برای حل آن توسط خودتان:

مثال 7

یک تابع داده شده است . تابع تداوم در نقاط را بررسی کنید. در صورت وجود، نقاط شکست را طبقه بندی کنید. طراحی را اجرا کنید.

سعی کنید تمام "کلمات" را به درستی "تلفظ" کنید =) و نمودار را به طور دقیق تر ترسیم کنید، دقت، در همه جا اضافی نخواهد بود؛-)

همانطور که به یاد دارید، توصیه می‌کنم فوراً نقشه را به عنوان پیش‌نویس تکمیل کنید، اما هر از گاهی با نمونه‌هایی مواجه می‌شوید که نمی‌توانید فوراً بفهمید که نمودار چگونه است. بنابراین، در تعدادی از موارد، سودمند است که ابتدا حدود یک طرفه را پیدا کنید و تنها پس از آن، بر اساس مطالعه، شاخه ها را به تصویر بکشید. در دو مثال پایانی همچنین تکنیکی را برای محاسبه محدودیت های یک طرفه یاد خواهیم گرفت:

مثال 8

تابع را از نظر پیوستگی بررسی کنید و نمودار شماتیک آن را بسازید.

راه حل: نقاط بد مشهود است: (مخرج نما را به صفر می رساند) و (مخرج کل کسر را به صفر می رساند). مشخص نیست نمودار این تابع چگونه است، یعنی بهتر است ابتدا کمی تحقیق کنید.

تعریف. تابع f(x) که در همسایگی نقطه x 0 تعریف شده است، فراخوانی می شود پیوسته در یک نقطه x 0 اگر حد تابع و مقدار آن در این نقطه برابر باشد، یعنی.

همین واقعیت را می توان متفاوت نوشت:

تعریف. اگر تابع f(x) در محله ای از نقطه x 0 تعریف شده باشد، اما در خود نقطه x 0 پیوسته نباشد، آنگاه فراخوانی می شود. مواد منفجرهتابع، و نقطه x 0 نقطه ناپیوستگی است.

مثالی از تابع پیوسته:

y

0 x 0 - x 0 x 0 + x

پ مثالی از یک تابع ناپیوسته:

تعریف. تابع f(x) در نقطه x 0 پیوسته نامیده می شود اگر برای هر عدد مثبت >0 عدد >0 وجود داشته باشد به طوری که برای هر x که شرط را برآورده کند.

نابرابری درست است
.

تعریف. تابع f(x) فراخوانی می شود مستمردر نقطه x = x 0، اگر افزایش تابع در نقطه x 0 یک مقدار بی نهایت کوچک باشد.

f(x) = f(x 0) + (x)

که در آن (x) در xx 0 بینهایت کوچک است.

که در آن a(x) در x®x0 بی نهایت کوچک است.

1) مجموع، تفاوت و حاصلضرب توابع پیوسته در نقطه x 0 تابعی است پیوسته در نقطه x 0.

2) ضریب دو تابع پیوسته - یک تابع پیوسته است به شرطی که g(x) در نقطه x 0 برابر با صفر نباشد.

3) برهم نهی توابع پیوسته یک تابع پیوسته است.

این ویژگی را می توان به صورت زیر نوشت:

اگر u = f(x)، v = g(x) توابع پیوسته در نقطه x = x 0 باشند، آنگاه تابع v = g(f(x)) نیز در این نقطه یک تابع پیوسته است.

با استفاده از قضایای حدی می توان صحت ویژگی های فوق را به راحتی اثبات کرد.

تداوم برخی از توابع ابتدایی.

1) تابع f(x) = C، C = const یک تابع پیوسته در کل دامنه تعریف است.

2) عملکرد منطقی
برای تمام مقادیر x به جز مقادیری که مخرج صفر می شود، پیوسته است. بنابراین، تابعی از این نوع در کل دامنه تعریف پیوسته است.

3) توابع مثلثاتی sin و cos در محدوده تعریف خود پیوسته هستند.

اجازه دهید ویژگی 3 را برای تابع y = sinx ثابت کنیم.

اجازه دهید افزایش تابع y = sin(x + x) – sinx یا بعد از تبدیل را بنویسیم:

در واقع، برای حاصل ضرب دو تابع محدودیتی وجود دارد
و
. در این حالت، تابع کسینوس یک تابع محدود در х0 است
، و به دلیل

حد تابع سینوس
، سپس درх0 بینهایت کوچک است.

بنابراین، حاصلضرب یک تابع محدود و یک تابع بی‌نهایت کوچک وجود دارد، بنابراین این محصول، یعنی. تابع у بی نهایت کوچک است. مطابق با تعاریفی که در بالا توضیح داده شد، تابع y = sinx یک تابع پیوسته برای هر مقدار x = x 0 از دامنه تعریف است، زیرا افزایش آن در این نقطه یک مقدار بی نهایت کوچک است.

نقاط شکست و طبقه بندی آنها.

بیایید تابع f(x) را در همسایگی نقطه x 0 در نظر بگیریم، به استثنای خود این نقطه. از تعریف نقطه شکست یک تابع نتیجه می شود که اگر تابع در این نقطه تعریف نشده باشد یا در آن پیوسته نباشد، x = x 0 نقطه شکست است.

همچنین باید توجه داشت که تداوم یک تابع می تواند یک طرفه باشد. اجازه دهید این را به شرح زیر توضیح دهیم.

، سپس تابع را راست پیوسته می گویند.

اگر محدودیت یک طرفه (به بالا مراجعه کنید)
، سپس گفته می شود که تابع پیوسته باقی می ماند.

تعریف. نقطه x 0 نامیده می شود نقطه شکستتابع f(x)، اگر f(x) در نقطه x 0 تعریف نشده باشد یا در این نقطه پیوسته نباشد.

تعریف. نقطه x 0 نامیده می شود نقطه ناپیوستگی از نوع 1، اگر در این نقطه تابع f(x) دارای حدهای چپ و راست محدود، اما مساوی نیست.

برای احراز شرایط این تعریف، لازم نیست تابع در نقطه x = x 0 تعریف شود، کافی است که در سمت چپ و راست آن تعریف شود.

از تعریف می توان نتیجه گرفت که در نقطه ناپیوستگی نوع اول یک تابع فقط می تواند یک پرش محدود داشته باشد. در برخی موارد خاص، گاهی اوقات نقطه ناپیوستگی نوع 1 نیز نامیده می شود قابل جابجایینقطه شکست، اما در زیر بیشتر در مورد این صحبت خواهیم کرد.

تعریف. نقطه x 0 نامیده می شود نقطه ناپیوستگی از نوع 2، اگر در این مرحله تابع f(x) حداقل یکی از حدهای یک طرفه را نداشته باشد یا حداقل یکی از آنها نامحدود باشد.

تداوم یک تابع در یک بازه و یک قطعه.

تعریف. تابع f(x) فراخوانی می شود پیوسته در یک بازه (بخش)، اگر در هر نقطه از بازه (بخش) پیوسته باشد.

در این حالت، تداوم تابع در انتهای یک قطعه یا بازه مورد نیاز نیست.

خواص توابع پیوسته در یک بازه.

خاصیت 1: (قضیه اول وایرشتراس (Carl Weierstrass (1815-1897) - ریاضیدان آلمانی)). تابعی که در یک بازه پیوسته است در این بازه محدود می شود، یعنی. شرط –M  f(x)  M بر روی قطعه ارضا می شود.

اثبات این خاصیت بر اساس این واقعیت است که تابعی که در نقطه x 0 پیوسته است در یک همسایگی مشخص از آن محدود شده است و اگر قطعه را به تعداد نامتناهی قطعه تقسیم کنید که تا نقطه "انقباض" هستند. x 0، سپس یک همسایگی مشخص از نقطه x 0 تشکیل می شود.

خاصیت 2: تابعی که روی قطعه پیوسته است، بزرگترین و کوچکترین مقادیر را روی آن می گیرد.

آن ها مقادیر x 1 و x 2 وجود دارد به طوری که f(x 1) = m، f(x 2) = M، و

m  f(x)  M

آن ها مقادیر x1 و x2 وجود دارد به طوری که f(x1) = m، f(x2) = M، و

تفاوت بین بزرگترین و کوچکترین مقدار یک تابع در یک قطعه نامیده می شود تردیدتوابع روی یک بخش

خاصیت 3: (قضیه دوم بولزانو-کوشی). تابعی که در بازه پیوسته است، تمام مقادیر بین دو مقدار دلخواه را در این بازه می گیرد.

خاصیت 4: اگر تابع f(x) در نقطه x = x 0 پیوسته باشد، آنگاه مقداری همسایگی نقطه x 0 وجود دارد که در آن تابع علامت خود را حفظ می کند.

خاصیت 5: (قضیه اول بولزانو (1781-1848) - کوشی). اگر یک تابع f(x) روی یک قطعه پیوسته باشد و دارای مقادیری از علائم متضاد در انتهای قطعه باشد، آنگاه نقطه ای در داخل این قطعه وجود دارد که f(x) = 0 است.

آن ها اگر علامت(f(a))  علامت(f(b))، سپس  x 0: f(x 0) = 0.

مثال.

در نقطه x = -1 تابع در نقطه x = 1 نقطه ناپیوستگی از نوع اول پیوسته است

در

مثال.تابع را برای پیوستگی بررسی کنید و نوع نقاط ناپیوستگی را در صورت وجود تعیین کنید.

در نقطه x = 0 تابع در نقطه x = 1 نقطه ناپیوستگی از نوع اول پیوسته است