Predavanje 4.

Kontinuitet funkcija

1. Kontinuitet funkcije u tački

Definicija 1. Neka funkcija y=f(x) je definiran u tački X 0 iu nekom susjedstvu ove tačke. Funkcija y=f(x) se zove kontinuirano u tački x 0 , ako u ovoj tački postoji granica funkcije i ona je jednaka vrijednosti funkcije u ovoj tački, tj.

Dakle, uslov za kontinuitet funkcije y=f(x) u tački X 0 je li to:

Jer
, tada se jednakost (32) može zapisati u obliku

(33)

To znači da kada nalaženje granice neprekidne funkcijef(x) može se ići do granice pod znakom funkcije, tj. u funkciju f(x) umjesto argumenta X zamijeniti njegovu graničnu vrijednost X 0 .

lim sin x=sin(lim x);

lim arctg x=arctg(lim x); (34)

lim log x=log(lim x).

Vježbajte. Pronađite granicu: 1)
; 2)
.

Definirajmo kontinuitet funkcije na osnovu koncepata inkrementa argumenta i funkcije.

Jer uslovima
I
su identične (slika 4), tada jednakost (32) ima oblik:

ili
.

Definicija 2. Funkcija y=f(x) se zove kontinuirano u tački x 0 , ako je definisan u nekoj tački X 0 i njegovu okolinu, a beskonačno mali prirast u argumentu odgovara beskonačno malom inkrementu funkcije.

Vježbajte. Ispitati kontinuitet funkcije y=2X 2 1.

Svojstva funkcija kontinuiranih u tački

1. Ako su funkcije f(x) I φ (x) su kontinuirani u tački X 0, zatim njihov zbir
, posao
i privatno
(s obzirom na to
) su funkcije kontinuirane u tački X 0 .

2. Ako je funkcija at=f(x) je kontinuiran u tački X 0 i f(x 0)>0, onda postoji takva okolina tačke X 0 , u kojem f(x)>0.

3. Ako je funkcija at=f(u) je kontinuirana u tački u 0 , a funkcija u= φ (x) je kontinuiran u tački u 0 = φ (x 0 ), zatim složena funkcija y=f[φ (x)] je kontinuiran u tački X 0 .

2. Kontinuitet funkcije u intervalu i na segmentu

Funkcija y=f(x) se zove kontinuirano u intervalu (a; b), ako je kontinuirano u svakoj tački ovog intervala.

Funkcija y=f(x) se zove kontinuirano na segmentu [a; b] ako je kontinuiran u intervalu ( a; b), i u tački X=A je pravo kontinuirano (tj.
), i u tački x=b je ostavljeno kontinuirano (tj.
).

3. Tačke diskontinuiteta funkcije i njihova klasifikacija

Pozivaju se tačke u kojima se prekida kontinuitet funkcije tačke prekida ovu funkciju.

Ako X=X 0 – tačka prekida funkcije y=f(x), tada barem jedan od uslova prve definicije kontinuiteta funkcije nije zadovoljen.

Primjer.

1.
. 2.

3)
4)
.

▼Prelomna tačka X 0 se zove tačka prekida prva vrsta funkcije y=f(x), ako u ovoj tački postoje konačne granice funkcije s lijeve i desne strane (jednostrane granice), tj.
I
. pri čemu:

Magnituda | A 1 -A 2 | pozvao funkcija skok na tački diskontinuiteta prve vrste. ▲

▼Prelomna tačka X 0 se zove tačka prekida druga vrsta funkcije y=f(x), ako barem jedna od jednostranih granica (lijeva ili desna) ne postoji ili je jednaka beskonačnosti. ▲

Vježbajte. Pronađite prijelomne točke i saznajte njihov tip za funkcije:

1)
; 2)
.

4. Osnovne teoreme o kontinuiranim funkcijama

Teoreme o kontinuitetu funkcija slijede direktno iz odgovarajućih teorema o granicama.

Teorema 1. Zbir, proizvod i količnik dvije kontinuirane funkcije je kontinuirana funkcija (za količnik, osim za one vrijednosti argumenta u kojima djelitelj nije jednak nuli).

Teorema 2. Neka funkcije u=φ (x) je kontinuiran u tački X 0 i funkciju y=f(u) je kontinuiran u tački u=φ (x 0 ). Zatim kompleksna funkcija f(φ (x)), koji se sastoji od kontinuiranih funkcija, kontinuirano je u tački X 0 .

Teorema 3. Ako je funkcija y=f(x) je kontinuiran i striktno monoton na [ a; b] osovine Oh, zatim inverzna funkcija at=φ (x) je također kontinuiran i monoton na odgovarajućem segmentu [ c;d] osovine OU.

Bilo koji elementarna funkcija kontinuirano u svakoj tački u kojoj je definisano.

5. Svojstva funkcija kontinuiranih na intervalu

Weierstrassova teorema. Ako je funkcija kontinuirana na segmentu, tada dostiže maksimalnu i minimalnu vrijednost na ovom segmentu.

Posljedica. Ako je funkcija kontinuirana na intervalu, onda je ograničena na interval.

Bolzano-Cauchy teorema. Ako je funkcija y=f(x) je kontinuiran na intervalu [ a; b] i uzima nejednake vrijednosti na svojim krajevima f(a)=A I f(b)=B,
, onda koji god da je broj WITH, zaključeno između A I IN, postoji poenta
takav da f(c)=C.

Geometrijski teorema je očigledna. Za bilo koji broj WITH, zaključeno između A I IN, postoji tačka c unutar ovog segmenta tako da f(WITH)=C. Pravo at=WITH siječe graf funkcije u najmanje jednoj tački.

Posljedica. Ako je funkcija y=f(x) je kontinuiran na intervalu [ a; b] i poprima vrijednosti različitih predznaka na svojim krajevima, zatim unutar segmenta [ a; b] postoji barem jedna tačka With, u kojem je funkcija y=f(x) ide na nulu: f(c)=0.

Geometrijski značenje teoreme: ako graf neprekidne funkcije prolazi s jedne strane ose Oh na drugu, tada siječe osu Oh.

Kontinuitet funkcije u tački

Neka je funkcija f(x) definirana u nekom susjedstvu O(x0) tačke x0 (uključujući i samu tačku x0).

Funkcija f(x) naziva se kontinuiranom u tački x0 ako postoji limx → x0 f(x) jednaka vrijednosti funkcije f(x) u ovoj tački: lim

f(x) = f(x0), (1)

one. " O(f(x0)) $ O(x0) : x O O(x0) Yu f(x) O O(f(x0)) .

Komentar. Jednakost (1) se može zapisati kao: lim

one. pod znakom kontinuirane funkcije može se ići do granice.

Neka je Δx = x − x0 prirast argumenta, Δy = f(x) − f(x0) odgovarajući prirast funkcije.

Neophodan i dovoljno stanje kontinuitet funkcije u tački

Funkcija y = f(x) je kontinuirana na x0 ako i samo ako

Komentar. Uslov (2) se može tumačiti kao druga definicija kontinuiteta funkcije u tački. Obje definicije su ekvivalentne.

Neka je funkcija f(x) definirana u poluintervalu.

Kaže se da je funkcija f(x) ostavljena kontinuirano na x0 ako postoji jednostrani limit lim

Kontinuitet zbira, proizvoda i količnika dvije kontinuirane funkcije

Teorema 1. Ako su funkcije f(x) i g(x) kontinuirane u tački x0, tada su f(x) ± g(x), f(x) g(x), f(x) kontinuirane u ovoj tačka

Kontinuitet složene funkcije

Teorema 2. Ako je funkcija u(x) kontinuirana u tački x0, a funkcija f(u) kontinuirana u odgovarajućoj tački u0 = f(x0), onda je kompleksna funkcija f(u(x)) kontinuirana u tački x0.

Sve elementarne funkcije su kontinuirane u svakoj tački svog domena definicije.

Lokalna svojstva kontinuiranih funkcija

Teorema 3 (ograničenost kontinuirane funkcije). Ako je funkcija f(x) kontinuirana na x0, tada postoji susjedstvo O(x0) u kojem je f(x) ograničeno.

Dokaz slijedi iz tvrdnje o ograničenosti funkcije koja ima granicu.

Teorema 4 (stabilnost predznaka neprekidne funkcije). Ako je funkcija f(x) neprekidna u tački x0 i f(x0) ≠ 0, tada postoji susjedstvo tačke x0 u kojoj je f(x) ≠ 0, i znak f(x) u toj okolini poklapa se sa predznakom f(x0).

Klasifikacija tačaka prekida

Uslov (1) za kontinuitet funkcije f(x) u tački x0 je ekvivalentan uslovu f(x0 − 0) = f(x0 + 0) = f(x0), (3)

gdje je f(x 0 − 0) = lim

f(x) i f(x0 + 0) = lim

f(x) - jednostrane granice funkcije f(x) u tački x0.

Ako je uvjet (3) povrijeđen, tačka x0 se naziva tačka diskontinuiteta funkcije f(x). U zavisnosti od vrste povrede uslova (3), tačke prekida imaju različitu prirodu i klasifikuju se na sledeći način:

1. Ako u tački x0 postoje jednostrane granice f(x0 − 0), f (x0 + 0) i

f(x0 − 0) = f(x0 + 0) ≠ f(x0), tada se tačka x0 naziva uklonjiva tačka diskontinuiteta funkcije f(x) (slika 1).

Komentar. U tački x0 funkcija možda nije definirana.

2. Ako u tački x0 postoje jednostrane granice f(x0 − 0), f (x0 + 0) i

f(x0 − 0) ≠ f(x0 + 0), tada se tačka x0 naziva tačka diskontinuiteta sa konačnim skokom funkcije f(x) (slika 2).

Komentar. U tački diskontinuiteta sa konačnim skokom, vrijednost funkcije može biti bilo koja ili ne mora biti definirana.

Tačke uklonjivog diskontinuiteta i konačnog skoka nazivaju se diskontinuitetne tačke 1. vrste. Njihova žig je postojanje konačnih jednostranih granica f(x0 − 0) i

3. Ako je u tački x0 barem jedna od jednostranih granica f(x0 − 0), f (x0 + 0) jednaka beskonačnosti ili ne postoji, tada
x0 naziva se tačka diskontinuiteta 2. vrste (slika 3).

Ako je barem jedna od jednostranih granica f(x0 − 0), f (x0 + 0) jednaka beskonačnosti, tada se prava linija x = x 0 naziva vertikalna asimptota grafa funkcije y = f (x).

Definicija. Funkcija f(x), definirana u susjedstvu neke tačke x0, naziva se kontinuiranom u tački x0 ako su granica funkcije i njena vrijednost u ovoj tački jednaki, tj.

Ista činjenica se može drugačije napisati:

Definicija. Ako je funkcija f(x) definirana u nekom susjedstvu točke x0, ali nije kontinuirana u samoj tački x0, onda se naziva diskontinuirana funkcija, a točka x0 se naziva diskontinuitetnom tačkom.

Definicija. Za funkciju f(x) se kaže da je kontinuirana u točki x0 ako je za bilo koju pozitivan broj e>0 postoji broj D>0 takav da za bilo koje x koje zadovoljava uslov

nejednakost je tačna.

Definicija. Funkcija f(x) se naziva kontinuiranom u tački x = x0 ako je prirast funkcije u tački x0 infinitezimalna vrijednost.

f(x) = f(x0) + a(x)

gdje je a(x) infinitezimalna na x®x0.

Svojstva kontinuiranih funkcija.

1) Zbir, razlika i proizvod funkcija kontinuiranih u tački x0 je funkcija kontinuirana u tački x0.

2) Kvocijent dvije kontinuirane funkcije je kontinuirana funkcija pod uslovom da g(x) nije jednak nuli u tački x0.

3) Superpozicija kontinuiranih funkcija je kontinuirana funkcija.

Ovo svojstvo se može napisati na sljedeći način:

Ako su u = f(x), v = g(x) kontinuirane funkcije u tački x = x0, tada je funkcija v = g(f(x)) također kontinuirana funkcija u ovoj tački.

Validnost gornjih svojstava može se lako dokazati korištenjem graničnih teorema

Svojstva funkcija kontinuiranih na intervalu.

Svojstvo 1: (Prva Weierstrassova teorema (Weierstrass Karl (1815-1897) - njemački matematičar)). Funkcija koja je kontinuirana na intervalu je ograničena na ovaj interval, tj. uslov –M £ f(x) £ M je zadovoljen na segmentu.

Dokaz ovog svojstva zasniva se na činjenici da je funkcija koja je kontinuirana u tački x0 ograničena u određenom njenom susjedstvu, a ako segment podijelite na beskonačan broj segmenata koji su „kontraktirani“ u tačku x0 , tada se formira određena okolina tačke x0.

Svojstvo 2: Funkcija kontinuirana na segmentu uzima najveću i najmanju vrijednost na njemu.

One. postoje vrijednosti x1 i x2 takve da je f(x1) = m, f(x2) = M, i

Zabilježimo ove najveće i najmanje vrijednosti koje funkcija može uzeti segment nekoliko puta (na primjer, f(x) = sinx).

Razlika između najveće i najmanje vrijednosti funkcije na intervalu naziva se oscilacija funkcije na intervalu.

Svojstvo 3: (Druga Bolzano–Cauchyjeva teorema). Funkcija koja je kontinuirana na intervalu preuzima sve vrijednosti između dvije proizvoljne vrijednosti na ovom intervalu.

Svojstvo 4: Ako je funkcija f(x) kontinuirana u tački x = x0, tada postoji neka okolina tačke x0 u kojoj funkcija zadržava svoj predznak.

Svojstvo 5: (Prva Bolzanova teorema (1781-1848) – Cauchy). Ako je funkcija f(x) kontinuirana na segmentu i ima vrijednosti suprotnih predznaka na krajevima segmenta, tada postoji tačka unutar ovog segmenta u kojoj je f(x) = 0.

One. ako je sign(f(a)) ¹ sign(f(b)), onda je $ x0: f(x0) = 0.

Definicija. Kaže se da je funkcija f(x) uniformno kontinuirana na intervalu ako za bilo koje e>0 postoji D>0 takav da je za bilo koje točke x1Î i x2Î takve da

ïx2 – x1ï< D

nejednakost ïf(x2) – f(x1)ï je tačna< e

Razlika između uniformnog kontinuiteta i „običnog“ kontinuiteta je u tome što za bilo koje e postoji svoj D, nezavisno od x, a sa „običnim“ kontinuitetom D zavisi od e i x.

Svojstvo 6: Kantorova teorema (Georg Cantor (1845-1918) - njemački matematičar). Funkcija kontinuirana na segmentu je uniformno neprekidna na njemu.

(Ovo svojstvo vrijedi samo za segmente, a ne za intervale i poluintervale.)

Definicija kontinuiteta

Funkcija f (x) se naziva kontinuiranom u tački a ako je: f () pp

1) funkcija f(x) je definirana u tački a,

2) ima konačnu granicu kao x→ a 2) ima konačnu granicu kao x→ a,

3) ova granica je jednaka vrijednosti funkcije u ovoj tački:

Kontinuitet u intervalu

Za funkciju f (x) se kaže da je kontinuirana na intervalu X ako je f () pp ru

Ona je kontinuirana u svakoj tački ovog intervala.

Izjava. Sve elementarne funkcije su kontinuirane u

Područja njihove definicije.

Ograničena funkcija

Za funkciju se kaže da je ograničena na interval if

postoji broj M takav da je za sve x ∈

nejednakost:| f(x)| ≤ M.

Weierstrassove dvije teoreme

Weierstrassova prva teorema. Ako je funkcija f (x r r r r f f (

je kontinuiran na segmentu, onda je ograničen na ovaj segment

Weierstrassova druga teorema. Ako je funkcija f(x

je kontinuirana na segmentu, onda dolazi do ovog segmenta

najmanja vrijednost m i najveća vrijednost M.

Bolzano-Cauchy teorema

Ako je funkcija f (x) kontinuirana na segmentu vrijednosti na f f () pp p

na krajevima ovog segmenta f(a) i f(b) imaju suprotne predznake,

Unutar segmenta nalazi se tačka c∈ (a,b) takva da je f (c) = 0. ur p () f ()

Kontinuitet funkcije. Prelomne tačke.

Bik hoda, njiše se, uzdiše dok ide:
- Ma, tabla je na izmaku, sad ću pasti!

U ovoj lekciji ćemo ispitati koncept kontinuiteta funkcije, klasifikaciju tačaka diskontinuiteta i uobičajene praktični problem studije kontinuiteta funkcija. Već iz samog naziva teme mnogi intuitivno pogađaju o čemu će biti riječi i misle da je materijal prilično jednostavan. Istina je. Ali jednostavni zadaci se najčešće kažnjavaju zbog zanemarivanja i površnog pristupa njihovom rješavanju. Stoga vam preporučujem da vrlo pažljivo proučite članak i uhvatite sve suptilnosti i tehnike.

Šta treba da znate i umete da radite? Ne baš puno. Da biste dobro naučili lekciju, morate razumjeti šta je to granica funkcije . Za čitaoce sa niskim nivoom pripreme dovoljno je da shvate članak Ograničenja funkcija. Primjeri rješenja i da pogledam geometrijsko značenje ograničenje u priručniku Grafovi i svojstva elementarnih funkcija . Takođe je preporučljivo da se upoznate geometrijske transformacije grafova , budući da praksa u većini slučajeva uključuje izradu crteža. Izgledi su optimistični za sve, a čak i pun čajnik moći će se sam nositi sa zadatkom u narednih sat-dva!

Kontinuitet funkcije. Prelomne tačke i njihova klasifikacija

Koncept kontinuiteta funkcije

Razmotrimo neku funkciju koja je kontinuirana na cijeloj brojevnoj pravoj:

Ili, sažetije rečeno, naša funkcija je kontinuirana na (skup realnih brojeva).

Šta je „filistički“ kriterijum kontinuiteta? Očigledno, graf kontinuirane funkcije može se nacrtati bez podizanja olovke sa papira.

U ovom slučaju treba jasno razlikovati dva jednostavna koncepta: domenu funkcije I kontinuitet funkcije. Uglavnom to nije ista stvar. Na primjer:

Ova funkcija definirana na cijeloj brojevnoj pravoj, odnosno za svima Značenje “x” ima svoje značenje za “y”. Konkretno, ako , Tada . Imajte na umu da je druga tačka punktuirana, jer po definiciji funkcije vrijednost argumenta mora odgovarati jedina stvar vrijednost funkcije. dakle, domena naša funkcija: .

kako god ova funkcija nije kontinuirano uključena! Sasvim je očigledno da u tom trenutku ona pati jaz. Termin je također prilično razumljiv i vizualan, ovdje će se olovka ionako morati otkinuti s papira. Malo kasnije ćemo pogledati klasifikaciju tačaka prekida.

Kontinuitet funkcije u tački i na intervalu

Na ovaj ili onaj način matematički problem možemo govoriti o kontinuitetu funkcije u tački, kontinuitetu funkcije na intervalu, poluintervalu ili kontinuitetu funkcije na segmentu. To je, ne postoji "puki kontinuitet"– funkcija može biti kontinuirana NEGDJE. A temeljni "građevinski blok" svega ostalog je kontinuitet funkcije u tački .

Teorija matematička analiza daje definiciju kontinuiteta funkcije u tački koristeći “delta” i “epsilon” susjedstva, ali u praksi se koristi druga definicija na koju ćemo obratiti veliku pažnju.

Prvo da se podsetimo jednostrane granice koji je upao u naše živote na prvoj lekciji o grafovima funkcija . Razmotrite svakodnevnu situaciju:

Ako se osi približimo tački lijevo(crvena strelica), tada će odgovarajuće vrijednosti "igara" ići duž ose do tačke (grimizna strelica). Matematički, ova činjenica se fiksira pomoću lijeva granica:

Obratite pažnju na unos (čita se “x teži ka ka na lijevoj strani”). “Aditiv” “minus nula” simbolizira , u suštini to znači da se broju približavamo s lijeve strane.

Slično, ako se približite tački "ka" desno(plava strelica), tada će "igre" doći na istu vrijednost, ali duž zelene strelice, i desna granicaće biti formatiran na sljedeći način:

"Additiv" simbolizira , a unos glasi: "x teži ka ka na desnoj strani."

Ako su jednostrane granice konačne i jednake(kao u našem slučaju): , onda ćemo reći da postoji GENERALNA granica. Jednostavno je, opšta granica je naše "uobičajeno" granica funkcije , jednako konačnom broju.

Imajte na umu da ako funkcija nije definirana na (izbacite crnu tačku na grani grafa), onda gornji proračuni ostaju važeći. Kao što je već nekoliko puta navedeno, posebno u članku na infinitezimalnim funkcijama , izrazi znače da je "x" beskonačno blizu približava tački, dok NIJE VAŽNO, bez obzira da li je sama funkcija definirana u datoj točki ili ne. Dobar primjerće se pojaviti u sljedećem pasusu, kada se funkcija analizira.

Definicija: funkcija je kontinuirana u točki ako je granica funkcije u datoj tački jednaka vrijednosti funkcije u toj tački: .

Definicija je detaljna u sljedećim terminima:

1) Funkcija mora biti definirana u tački, odnosno vrijednost mora postojati.

2) Mora postojati opšta granica funkcije. Kao što je gore navedeno, ovo implicira postojanje i jednakost jednostranih granica: .

3) Granica funkcije u datoj tački mora biti jednaka vrijednosti funkcije u ovoj tački: .

Ako se prekrši najmanje jedan od tri uslova, tada funkcija gubi svojstvo kontinuiteta u tački .

Kontinuitet funkcije u intervalu je formulisan genijalno i vrlo jednostavno: funkcija je kontinuirana na intervalu ako je kontinuirana u svakoj tački datog intervala.

Konkretno, mnoge funkcije su kontinuirane na beskonačnom intervalu, odnosno na skupu realnih brojeva. Ovo je linearna funkcija, polinomi, eksponencijalni, sinusni, kosinusni, itd. I općenito, bilo koji elementarna funkcija kontinuirano na svom domenu definicije , na primjer, logaritamska funkcija je kontinuirana na intervalu . nadam se u ovom momentu imate prilično dobru ideju o tome kako izgledaju grafikoni glavnih funkcija. Više detaljne informacije može se zaključiti njihov kontinuitet ljubazna osoba po prezimenu Fichtengolts.

Uz kontinuitet funkcije na segmentu i poluintervali, također sve nije teško, ali je prikladnije razgovarati o tome na času o pronalaženju minimalne i maksimalne vrijednosti funkcije na segmentu , ali za sada nemojmo brinuti o tome.

Klasifikacija tačaka prekida

Fascinantan život funkcija bogat je raznim posebnim točkama, a tačke prekida samo su jedna od stranica njihove biografije.

Bilješka : za svaki slučaj, zadržaću se na jednoj elementarnoj stvari: tačka preloma je uvek jedna tačka– ne postoji „nekoliko tačaka prekida u nizu“, odnosno ne postoji „interval pauze“.

Ove točke su pak podijeljene u dvije velike grupe: rupture prve vrste I rupture druge vrste. Svaka vrsta jaza ima svoje karakteristike koje ćemo sada pogledati:

Tačka diskontinuiteta prve vrste

Ako je uslov kontinuiteta narušen u nekoj tački i jednostrane granice konačan , onda se zove tačka diskontinuiteta prve vrste.

Počnimo s najoptimističnijim slučajem. Prema prvobitnoj ideji lekcije, htio sam ispričati teoriju „u opšti pogled“, ali da bih demonstrirao realnost materijala, odlučio sam se na opciju sa određenim likovima.

Tužno je, poput fotografije mladenaca na pozadini Vječne vatre, ali sljedeći snimak je općenito prihvaćen. Hajde da prikažemo graf funkcije na crtežu:


Ova funkcija je kontinuirana na cijeloj brojevnoj pravoj, osim na tački. I u stvari, imenilac ne može biti jednak nuli. Međutim, u skladu sa značenjem granice, možemo beskonačno blizu pristup „nuli“ i slijeva i s desna, odnosno jednostrane granice postoje i, očigledno, poklapaju se:
(Uslov br. 2 kontinuiteta je zadovoljen).

Ali funkcija nije definirana u tački, stoga je uvjet br. 1 kontinuiteta narušen i funkcija trpi diskontinuitet u ovoj tački.

Prekid ovog tipa (sa postojećim opšta granica) su pozvani popravljiv jaz. Zašto se može ukloniti? Jer funkcija može redefinisati na prelomnoj tački:

Da li izgleda čudno? Možda. Ali takva notacija funkcije ne proturječi ničemu! Sada je jaz zatvoren i svi su zadovoljni:


Izvršimo formalnu provjeru:

2) – postoji opšta granica;
3)

Dakle, sva tri uslova su zadovoljena, a funkcija je neprekidna u tački prema definiciji kontinuiteta funkcije u tački.

Međutim, matan mrzitelji mogu, na primjer, definirati funkciju na loš način :


Zanimljivo je da su ovde zadovoljena prva dva uslova kontinuiteta:
1) – funkcija je definisana u datoj tački;
2) – postoji opšta granica.

Ali treća granica nije prijeđena: , odnosno granica funkcije u tački nije jednako vrijednost date funkcije u datoj tački.

Dakle, u jednom trenutku funkcija trpi diskontinuitet.

Drugi, tužniji slučaj se zove ruptura prve vrste sa skokom. A tugu izazivaju jednostrane granice koje konačan i različit. Primjer je prikazan na drugom crtežu lekcije. Takav jaz se obično javlja u djelomično definirane funkcije, koji su već spomenuti u članku o transformacijama grafova .

Razmotrite funkciju po komadima a mi ćemo završiti njegov crtež. Kako napraviti grafikon? Veoma jednostavno. Na poluintervalu crtamo fragment parabole ( zelene boje), na intervalu – pravi segment (crveno) i na poluintervali – prava linija (plavo).

Štoviše, zbog nejednakosti, vrijednost je određena za kvadratnu funkciju (zelena tačka), a zbog nejednakosti vrijednost je određena za linearnu funkciju (plava tačka):

U najtežem slučaju, trebalo bi da pribegnete konstrukciji tačku po tačku svakog dela grafa (pogledajte prvi lekcija o grafovima funkcija ).

Sada će nas zanimati samo poenta. Hajde da ga ispitamo radi kontinuiteta:

2) Izračunajmo jednostrane granice.

Na lijevoj strani imamo segment crvene linije, tako da je lijevo ograničenje:

Na desnoj strani je plava ravna linija i desna granica:

Kao rezultat, dobili smo konačni brojevi, i oni nije jednako. Od jednostranih granica konačan i različit: , onda naša funkcija toleriše diskontinuitet prve vrste sa skokom.

Logično je da se jaz ne može eliminisati – funkcija se zaista ne može dalje definirati i „zalijepiti zajedno“, kao u prethodnom primjeru.

Tačke diskontinuiteta druge vrste

Obično se svi ostali slučajevi rupture pametno svrstavaju u ovu kategoriju. Neću sve nabrajati, jer ćete u praksi u 99% problema naići beskrajni jaz– kada ste ljevoruk ili dešnjak, a češće, obje granice su beskonačne.

I, naravno, najočitija slika je hiperbola u tački nula. Ovdje su obje jednostrane granice beskonačne: , dakle, funkcija trpi diskontinuitet druge vrste u točki .

Trudim se da svoje članke ispunim što raznovrsnijim sadržajem, pa pogledajmo graf funkcije koja još nije naišla:

prema standardnoj shemi:

1) Funkcija nije definirana u ovom trenutku jer nazivnik ide na nulu.

Naravno, odmah možemo zaključiti da funkcija trpi diskontinuitet u tački , ali bi bilo dobro klasificirati prirodu diskontinuiteta, što je često potrebno uslovom. Za ovo:

Da vas podsjetim da pod snimanjem mislimo beskonačno mali negativan broj, a ispod unosa - beskonačno mali pozitivan broj.

Jednostrane granice su beskonačne, što znači da funkcija trpi diskontinuitet 2. vrste u tački . Y-osa je vertikalna asimptota za grafikon.

Nije neuobičajeno da postoje obje jednostrane granice, ali samo jedna od njih je beskonačna, na primjer:

Ovo je graf funkcije.

Ispitujemo poentu za kontinuitet:

1) Funkcija nije definirana u ovom trenutku.

2) Izračunajmo jednostrane granice: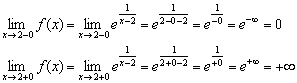

O načinu izračunavanja ovakvih jednostranih granica govorit ćemo u posljednja dva primjera predavanja, iako su mnogi čitaoci već sve vidjeli i pogodili.

Lijeva granica je konačna i jednaka nuli (mi "ne idemo do same tačke"), ali desna granica je beskonačna i narandžasta grana grafa se približava beskonačno blizu svoje vertikalna asimptota , dato jednadžbom (crna tačkasta linija).

Dakle, funkcija pati diskontinuitet druge vrste u tački .

Što se tiče diskontinuiteta 1. vrste, funkcija se može definirati u samoj tački diskontinuiteta. Na primjer, za funkciju po komadima Slobodno stavite crnu podebljanu tačku na početak koordinata. Desno je grana hiperbole, a desna granica je beskonačna. Mislim da skoro svi imaju ideju kako ovaj grafikon izgleda.

Čemu su se svi radovali:

Kako ispitati funkciju za kontinuitet?

Proučavanje funkcije za kontinuitet u nekoj tački provodi se prema već utvrđenoj rutinskoj šemi, koja se sastoji od provjere tri uvjeta kontinuiteta:

Primjer 1

Funkcija istraživanja

Rješenje:

1) Jedina tačka unutar opsega je gdje funkcija nije definirana.

2) Izračunajmo jednostrane granice:

Jednostrane granice su konačne i jednake.

Dakle, u trenutku kada funkcija trpi diskontinuitet koji se može ukloniti.

Kako izgleda graf ove funkcije?

Želeo bih da pojednostavim , i čini se da se dobija obična parabola. ALI originalna funkcija nije definirana u točki, pa je potrebna sljedeća klauzula:

Napravimo crtež:

Odgovori: funkcija je kontinuirana na cijeloj brojevnoj pravoj osim točke u kojoj trpi diskontinuitet koji se može ukloniti.

Funkcija se može dalje definirati na dobar ili ne tako dobar način, ali prema uvjetu to nije potrebno.

Kažete da je ovo nategnut primjer? Ne sve. To se u praksi dogodilo na desetine puta. Gotovo svi zadaci stranice proizlaze iz stvarnog samostalnog rada i testova.

Riješimo se naših omiljenih modula:

Primjer 2

Funkcija istraživanja za kontinuitet. Odredite prirodu diskontinuiteta funkcije, ako postoje. Izvršite crtež.

Rješenje: Učenici se iz nekog razloga plaše i ne vole funkcije s modulom, iako u njima nema ništa komplikovano. Takvih stvari smo već malo dotakli u lekciji. Geometrijske transformacije grafova . Budući da je modul nenegativan, on se proširuje na sljedeći način: , gdje je “alfa” neki izraz. IN u ovom slučaju, a našu funkciju treba napisati po komadima:

Ali razlomci oba komada moraju se smanjiti za . Smanjenje, kao iu prethodnom primjeru, neće proći bez posljedica. Originalna funkcija nije definirana u tački jer nazivnik ide na nulu. Prema tome, sistem treba dodatno specificirati uslov , i učiniti prvu nejednakost strogom:

Sada o VEOMA KORISNOJ tehnici odlučivanja: prije finalizacije zadatka na nacrtu, poželjno je napraviti crtež (bez obzira da li to uvjeti zahtijevaju ili ne). Ovo će vam pomoći, prvo, da odmah vidite tačke kontinuiteta i tačke diskontinuiteta, i, drugo, 100% će vas zaštititi od grešaka pri pronalaženju jednostranih granica.

Hajde da crtamo. Prema našim proračunima, lijevo od tačke potrebno je nacrtati fragment parabole (plava boja), a desno - komadić parabole (crvena boja), dok funkcija nije definirana na sama poenta:

Ako ste u nedoumici, uzmite nekoliko x vrijednosti i priključite ih u funkciju (sjetite se da modul uništava mogući znak minus) i provjerite graf.

Hajde da analitički ispitamo funkciju za kontinuitet:

1) Funkcija nije definirana u tački, pa možemo odmah reći da u njoj nije kontinuirana.

2) Ustanovimo prirodu diskontinuiteta da bismo to uradili, izračunavamo jednostrane granice:

Jednostrane granice su konačne i različite, što znači da funkcija trpi diskontinuitet 1. vrste sa skokom u tački . Imajte na umu da prilikom pronalaženja granica nije važno da li je funkcija u tački prekida definirana ili ne.

Sada ostaje samo da prenesete crtež iz nacrta (napravljen je kao uz pomoć istraživanja ;-)) i završite zadatak:

Odgovori: funkcija je kontinuirana na cijeloj brojevnoj pravoj osim u tački u kojoj dolazi do prekida prve vrste sa skokom.

Ponekad zahtijevaju dodatnu indikaciju skoka diskontinuiteta. Izračunava se jednostavno - od desne granice treba oduzeti lijevu granicu: , odnosno u tački prekida naša funkcija je skočila 2 jedinice naniže (kao što nam govori znak minus).

Primjer 3

Funkcija istraživanja za kontinuitet. Odredite prirodu diskontinuiteta funkcije, ako postoje. Napravite crtež.

Ovo je primjer za nezavisna odluka, uzorak rješenja na kraju lekcije.

Prijeđimo na najpopularniju i najrašireniju verziju zadatka, kada se funkcija sastoji od tri dijela:

Primjer 4

Ispitajte funkciju za kontinuitet i nacrtajte graf funkcije .

Rješenje: očito je da su sva tri dijela funkcije kontinuirana na odgovarajućim intervalima, tako da ostaje provjeriti samo dvije točke “spojnice” između dijelova. Prvo, napravimo nacrt crteža, dovoljno sam detaljno prokomentirao tehniku ​​konstrukcije u prvom dijelu članka. Jedino što moramo pažljivo pratiti naše singularne tačke: zbog nejednakosti vrijednost pripada pravoj liniji (zelena tačka), a zbog nejednakosti vrijednost pripada paraboli (crvena tačka):


Pa, u principu, sve je jasno =) Ostaje samo formalizirati odluku. Za svaku od dvije „zglobne“ tačke, standardno provjeravamo 3 uvjeta kontinuiteta:

ja) Ispitujemo tačku za kontinuitet

1)

Jednostrane granice su konačne i različite, što znači da funkcija trpi diskontinuitet 1. vrste sa skokom u tački .

Izračunajmo skok diskontinuiteta kao razliku između desne i lijeve granice:
, odnosno graf je porastao za jednu jedinicu.

II) Ispitujemo tačku za kontinuitet

1) – funkcija je definirana u datoj točki.

2) Pronađite jednostrane granice:

– jednostrane granice su konačne i jednake, što znači da postoji opšta granica.

3) – granica funkcije u tački jednaka je vrijednosti ove funkcije u datoj tački.

U završnoj fazi crtež prenosimo na konačnu verziju, nakon čega stavljamo završni akord:

Odgovori: funkcija je kontinuirana duž cijele brojevne prave, osim tačke u kojoj dolazi do prekida prve vrste sa skokom.

Primjer 5

Ispitajte funkciju na kontinuitet i konstruirajte njen graf .

Ovo je primjer za samostalno rješenje, kratko rješenje i približan uzorak problema na kraju lekcije.

Možete steći utisak da u jednom trenutku funkcija mora biti kontinuirana, au drugom mora postojati diskontinuitet. U praksi to nije uvijek slučaj. Pokušajte ne zanemariti preostale primjere - bit će nekoliko zanimljivih i važnih karakteristika:

Primjer 6

Zadata funkcija . Istražite funkciju za kontinuitet u tačkama. Napravite graf.

Rješenje: i ponovo odmah izvršite crtež na nacrtu:

Posebnost ovog grafa je da je funkcija po komadima data jednadžbom apscisne ose. Ovo područje je ucrtano ovdje zeleno, a u bilježnici je obično označen podebljanim slovima jednostavnom olovkom. I, naravno, ne zaboravite na naše ovnove: vrijednost pripada tangentnoj grani (crvena tačka), a vrijednost pripada pravoj liniji.

Iz crteža je sve jasno - funkcija je kontinuirana duž cijele brojevne prave, ostaje samo formalizirati rješenje, koje se doslovno nakon 3-4 slična primjera dovodi do pune automatizacije:

ja) Ispitujemo tačku za kontinuitet

1) – funkcija je definirana u datoj tački.

2) Izračunajmo jednostrane granice:

, što znači da postoji opšta granica.

Za svaki slučaj, da vas podsjetim na trivijalnu činjenicu: granica konstante jednaka je samoj konstanti. U ovom slučaju, granica nule jednaka je samoj nuli (ljevoruka granica).

3) – granica funkcije u tački jednaka je vrijednosti ove funkcije u datoj tački.

Dakle, funkcija je neprekidna u tački prema definiciji kontinuiteta funkcije u tački.

II) Ispitujemo tačku za kontinuitet

1) – funkcija je definirana u datoj tački.

2) Pronađite jednostrane granice:

I ovdje – granica od jedan je jednaka samoj jedinici.

– postoji opšta granica.

3) – granica funkcije u tački jednaka je vrijednosti ove funkcije u datoj tački.

Dakle, funkcija je neprekidna u tački prema definiciji kontinuiteta funkcije u tački.

Kao i obično, nakon istraživanja prenosimo naš crtež u konačnu verziju.

Odgovori: funkcija je kontinuirana u tačkama.

Napominjemo da u tom stanju nismo pitali ništa o proučavanju cijele funkcije za kontinuitet, te se smatra dobrom matematičkom formom za formulisanje precizno i ​​jasno odgovor na postavljeno pitanje. Usput, ako uvjeti ne zahtijevaju da napravite graf, onda imate svako pravo da ga ne gradite (iako vas kasnije nastavnik može natjerati da to učinite).

Mala matematička vrtoglavica jezika za samostalno rješavanje:

Primjer 7

Zadata funkcija . Istražite funkciju za kontinuitet u tačkama. Klasifikujte prelomne tačke, ako ih ima. Izvršite crtež.

Pokušajte pravilno "izgovoriti" sve "riječi" =) I nacrtajte grafikon preciznije, tačnije, neće svugdje biti suvišno ;-)

Kao što se sjećate, preporučio sam da odmah završite crtež kao nacrt, ali s vremena na vrijeme naiđete na primjere u kojima ne možete odmah shvatiti kako graf izgleda. Stoga je u nekim slučajevima korisno prvo pronaći jednostrane granice i tek onda, na osnovu studije, prikazati grane. U zadnja dva primjera naučit ćemo i tehniku ​​za izračunavanje nekih jednostranih granica:

Primjer 8

Ispitajte funkciju za kontinuitet i konstruirajte njen shematski graf.

Rješenje: loše tačke su očigledne: (smanjuje nazivnik eksponenta na nulu) i (smanjuje imenilac cijelog razlomka na nulu). Nije jasno kako izgleda graf ove funkcije, što znači da je bolje prvo istražiti.

Definicija. Poziva se funkcija f(x), definirana u okolini neke tačke x 0 kontinuirano u jednoj tački x 0 ako su granica funkcije i njena vrijednost u ovoj tački jednaki, tj.

Ista činjenica se može drugačije napisati:

Definicija. Ako je funkcija f(x) definirana u nekom susjedstvu tačke x 0, ali nije kontinuirana u samoj tački x 0, onda se naziva eksplozivno funkcija, a tačka x 0 je tačka diskontinuiteta.

Primjer kontinuirane funkcije:

y

0 x 0 - x 0 x 0 + x

P primjer diskontinuirane funkcije:

Definicija. Funkcija f(x) se naziva kontinuiranom u tački x 0 ako za bilo koji pozitivan broj >0 postoji broj >0 takav da za bilo koji x koji zadovoljava uvjet

nejednakost istinita
.

Definicija. Poziva se funkcija f(x). kontinuirano u tački x = x 0, ako je prirast funkcije u tački x 0 infinitezimalna vrijednost.

f(x) = f(x 0) + (x)

gdje je (x) infinitezimalna na xx 0.

Svojstva kontinuiranih funkcija.

1) Zbir, razlika i proizvod funkcija kontinuiranih u tački x 0 je funkcija kontinuirana u tački x 0.

2) Kvocijent dvije neprekidne funkcije – je kontinuirana funkcija pod uvjetom da g(x) nije jednak nuli u tački x 0.

3) Superpozicija kontinuiranih funkcija je kontinuirana funkcija.

Ovo svojstvo se može napisati na sljedeći način:

Ako su u = f(x), v = g(x) kontinuirane funkcije u tački x = x 0, tada je funkcija v = g(f(x)) također kontinuirana funkcija u ovoj tački.

Validnost gornjih svojstava može se lako dokazati korištenjem graničnih teorema.

Kontinuitet nekih elementarnih funkcija.

1) Funkcija f(x) = C, C = const je kontinuirana funkcija u cijelom domenu definicije.

2) Racionalna funkcija
je kontinuiran za sve vrijednosti x osim onih kod kojih imenilac postaje nula. Dakle, funkcija ovog tipa je kontinuirana u cijelom domenu definicije.

3) Trigonometrijske funkcije sin i cos su kontinuirane u svom domenu definicije.

Dokažimo svojstvo 3 za funkciju y = sinx.

Zapišimo prirast funkcije y = sin(x + x) – sinx, ili nakon transformacije:

Zaista, postoji ograničenje za proizvod dvije funkcije
I
. U ovom slučaju, kosinusna funkcija je ograničena funkcija na h0
, i zato

granica sinusne funkcije
, onda je beskonačno mali nah0.

Dakle, postoji proizvod ograničene funkcije i infinitezimalnog, dakle ovaj proizvod, tj. funkcija u je beskonačno mala. U skladu sa definicijama o kojima se raspravljalo, funkcija y = sinx je kontinuirana funkcija za bilo koju vrijednost x = x 0 iz domene definicije, jer njegov prirast u ovoj tački je beskonačno mala vrijednost.

Prelomne tačke i njihova klasifikacija.

Razmotrimo neku funkciju f(x), kontinuiranu u okolini tačke x 0, sa mogućim izuzetkom same ove tačke. Iz definicije tačke prekida funkcije sledi da je x = x 0 tačka prekida ako funkcija nije definisana u ovoj tački ili nije kontinualna u njoj.

Također treba napomenuti da kontinuitet funkcije može biti jednostran. Objasnimo ovo na sljedeći način.

, tada se kaže da je funkcija desno kontinuirana.

Ako je jednostrano ograničenje (vidi gore)
, tada se kaže da je funkcija ostavljena kontinuirano.

Definicija. Tačka x 0 se zove tačka prekida funkcija f(x), ako f(x) nije definirana u tački x 0 ili nije kontinuirana u ovoj tački.

Definicija. Tačka x 0 se zove tačka diskontinuiteta 1. vrste, ako u ovom trenutku funkcija f(x) ima konačne, ali ne jednake, lijeve i desne granice.

Da bi se zadovoljili uslovi ove definicije, nije neophodno da funkcija bude definisana u tački x = x 0, dovoljno je da je definisana levo i desno od nje.

Iz definicije možemo zaključiti da u tački diskontinuiteta 1. vrste funkcija može imati samo konačan skok. U nekim posebnim slučajevima ponekad se naziva i tačka diskontinuiteta 1. vrste uklonjiv prelomna tačka, ali o tome ćemo više govoriti u nastavku.

Definicija. Tačka x 0 se zove tačka diskontinuiteta 2. vrste, ako u ovom trenutku funkcija f(x) nema barem jednu od jednostranih granica ili je barem jedna od njih beskonačna.

Kontinuitet funkcije na intervalu i na segmentu.

Definicija. Poziva se funkcija f(x). kontinuirano u intervalu (segmentu), ako je kontinuiran u bilo kojoj tački intervala (segmenta).

U ovom slučaju, kontinuitet funkcije na krajevima segmenta ili intervala nije potreban samo je potreban jednostrani kontinuitet na krajevima segmenta ili intervala.

Svojstva funkcija kontinuiranih na intervalu.

Nekretnina 1: (Prva Weierstrassova teorema (Carl Weierstrass (1815-1897) - njemački matematičar)). Funkcija koja je kontinuirana na intervalu je ograničena na ovaj interval, tj. uslov –M  f(x)  M je zadovoljen na segmentu.

Dokaz ovog svojstva zasniva se na činjenici da je funkcija koja je neprekidna u tački x 0 ograničena u određenom njenom susjedstvu, a ako segment podijelite na beskonačan broj segmenata koji su „kontraktirani“ na tačku x 0, tada se formira određena okolina tačke x 0.

Nekretnina 2: Funkcija koja je kontinuirana na segmentu uzima najveću i najmanju vrijednost na njemu.

One. postoje vrijednosti x 1 i x 2 takve da je f(x 1) = m, f(x 2) = M, i

m  f(x)  M

Zabilježimo ove najveće i najmanje vrijednosti koje funkcija može uzeti segment nekoliko puta (na primjer, f(x) = sinx).

Poziva se razlika između najveće i najmanje vrijednosti funkcije na segmentu oklevanje funkcije na segmentu.

Svojstvo 3: (Druga Bolzano–Cauchyjeva teorema). Funkcija koja je kontinuirana na intervalu preuzima sve vrijednosti između dvije proizvoljne vrijednosti na ovom intervalu.

Svojstvo 4: Ako je funkcija f(x) kontinuirana u tački x = x 0, tada postoji neka okolina tačke x 0 u kojoj funkcija zadržava svoj predznak.

Svojstvo 5: (Prva Bolzanova teorema (1781-1848) – Cauchy). Ako je funkcija f(x) kontinuirana na segmentu i ima vrijednosti suprotnih predznaka na krajevima segmenta, tada postoji tačka unutar ovog segmenta u kojoj je f(x) = 0.

One. ako je sign(f(a))  sign(f(b)), onda je  x 0: f(x 0) = 0.

Primjer.

u tački x = -1 funkcija je kontinuirana u tački x = 1 tačka diskontinuiteta 1. vrste

at

Primjer. Ispitajte funkciju za kontinuitet i odredite tip točaka diskontinuiteta, ako ih ima.

u tački x = 0 funkcija je kontinuirana u tački x = 1 tačka diskontinuiteta 1. vrste