Karakteristična jednačina. Korijeni karakteristične jednadžbe. Vremenske konstante. Vrijeme tranzicije. Metode za sastavljanje karakteristične jednačine Zašto vam je potrebna karakteristična jednačina
Karakteristična jednadžba se sastavlja za kolo nakon prebacivanja. Može se dobiti na sljedeće načine:
- direktno na osnovu diferencijalne jednačine oblika (2) (vidi predavanje br. 24), tj. isključivanjem iz sistema jednadžbi koje opisuju elektromagnetno stanje kola na osnovu prvog i drugog Kirchhoffovog zakona, svih nepoznatih veličina osim jedne, u odnosu na koju je napisana jednačina (2);
- korištenjem izraza za ulaznu impedanciju sinusoidnog strujnog kola;
- na osnovu izraza glavne determinante.
Prema prvoj metodi, u prethodnom predavanju dobijena je diferencijalna jednačina u vezi napona na kondenzatoru za serijski R-L-C kolo, na osnovu koje je napisana karakteristična jednačina.
Treba napomenuti da, budući da je linearni krug pokriven jednim prolaznim procesom, korijeni karakteristične jednadžbe su zajednički za sve slobodne komponente napona i struja grana kola, čiji su parametri uključeni u karakterističnu jednadžbu. Dakle, prema prvoj metodi sastavljanja karakteristične jednadžbe, bilo koja varijabla se može odabrati kao varijabla u odnosu na koju je zapisana.
Razmotrimo primjenu druge i treće metode sastavljanja karakteristične jednadžbe na primjeru kola na sl. 1.
Sastav karakteristične jednadžbe korištenjem metode ulaznog otpora je sljedeći:
je snimljen ulazna impedansa AC krugovi;
jw je zamijenjen operatorom p;
rezultirajući izraz je jednak nuli.
Jednačina
poklapa se sa karakterističnim.
Treba naglasiti da se ulazni otpor može zapisati u odnosu na tačku prekida bilo koje grane kola. U ovom slučaju, aktivna mreža s dva terminala zamjenjuje se pasivnom po analogiji s metodom ekvivalentnog generatora. Ova metoda sastavljanja karakteristične jednačine pretpostavlja odsustvo magnetno spregnutih grana u kolu; ako ih ima potrebno je izvršiti njihovo prethodno odvezivanje.
Za kolo na sl. 1 u odnosu na izvorne terminale
.
Zamjenom jw sa p i izjednačavanjem rezultirajućeg izraza sa nulom, pišemo
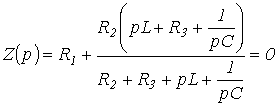
| . | (1) |
Prilikom sastavljanja karakteristične jednačine na osnovu izraza glavne determinante, broja algebarske jednačine, na osnovu kojeg se piše, jednak je broju nepoznatih komponenti slobodne struje. Algebraizacija originalnog sistema integro- diferencijalne jednadžbe, sastavljena, na primjer, na osnovu Kirchhoffovih zakona ili korištenjem metode struje petlje, izvodi se zamjenom simbola diferencijacije i integracije, respektivno, množenjem i dijeljenjem operatorom p. Karakteristična jednačina se dobija izjednačavanjem zapisane determinante sa nulom. Pošto izraz za glavnu determinantu ne zavisi od desnih strana sistema nehomogenih jednačina, može se sastaviti na osnovu sistema jednačina napisanih za ukupne struje.
Za kolo na sl. 1 algebraizirani sistem jednačina zasnovan na metodi strujne petlje ima oblik
Otuda i izraz za glavnu determinantu ovog sistema
Izjednačavajući D sa nulom, dobijamo rezultat sličan (1).
Opća metodologija za proračun prolaznih procesa klasičnom metodom
Općenito, metodologija za proračun prolaznih procesa klasičnom metodom uključuje sljedeće korake:
Primjeri proračuna prolaznih procesa klasičnom metodom
1. Prolazni procesi u R-L lanci kada je priključen na izvor napona
Takvi se procesi odvijaju, na primjer, pri povezivanju elektromagneta, transformatora, elektromotora itd. na izvor napajanja.
Razmotrimo dva slučaja:
Prema razmatranoj metodi za struju u kolu na sl. 2 se može napisati
Karakteristična jednačina
dakle vremenska konstanta 
.
dakle,
| . | (5) |
Zamjenom (4) i (5) u relaciju (3) pišemo
.
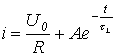Prema prvom zakonu komutacije. Onda
,
Dakle, struja u kolu tokom prelaznog procesa je opisana jednačinom
,
a napon na induktoru je dat sa
.
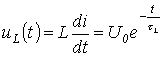Kvalitativni izgled krivulja i odgovarajući dobijena rješenja prikazana je na Sl. 3.
Za drugi tip izvora, prisilna komponenta se izračunava pomoću simboličke metode:
,
Izraz slobodne komponente ne zavisi od vrste izvora napona. dakle,
.
Od tada
Dakle, konačno dobijamo
| . | (6) |
Analiza rezultirajućeg izraza (6) pokazuje:
Ako je značajna po veličini, onda se tokom pola perioda slobodna komponenta ne smanjuje značajno. U ovom slučaju, maksimalna vrijednost prelazne struje može značajno premašiti amplitudu stabilne struje. Kao što se može videti sa sl. 4, gdje
, maksimalna struja se javlja nakon otprilike . U limitu na .
Dakle, za linearni krug, maksimalna vrijednost prolazne struje ne može premašiti dvostruku amplitudu prisilne struje: .
Slično za linearni krug s kondenzatorom: ako je u trenutku uključivanja prisilni napon jednak vrijednosti njegove amplitude i vremenska konstanta kola je dovoljno velika, tada nakon otprilike pola perioda napon na kondenzatoru dostiže svoju maksimalnu vrijednost , koji ne može premašiti dvostruku amplitudu prinudnog napona: 
.
2. Prolazni procesi pri odspajanju induktora iz izvora napajanja
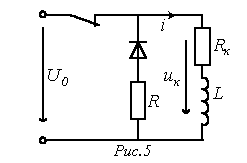
Kada se ključ otvori u kolu na sl. 5 prisilna komponenta struje kroz induktor.
Karakteristična jednačina
,
gdje 
I 
.
Prema prvom zakonu komutacije
.
Dakle, izraz za prolaznu struju je
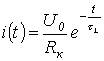
i napon na induktoru
 .
|
(7) |
Analiza (7) pokazuje da pri otvaranju kola sa induktivnim elementima može doći do velikih prenapona koji, bez preduzimanja posebnih mjera, mogu oštetiti opremu. Zaista, kada 
Naponski modul na induktoru u trenutku uključivanja bit će višestruko veći od napona izvora: . U nedostatku otpornika za gašenje R, navedeni napon se primjenjuje na otvorne kontakte ključa, zbog čega između njih nastaje luk.
3. Punjenje i pražnjenje kondenzatora
Kada se ključ pomeri u položaj 1 (vidi sliku 6), počinje proces punjenja kondenzatora:
.
Prisilna komponenta napona na kondenzatoru.
Iz karakteristične jednačine
korijen je određen 
. Otuda i vremenska konstanta.
Slobodni način rada kola ne ovisi o izvorima energije, određen je samo strukturom kruga i parametrima njegovih elemenata. Iz ovoga slijedi da će korijeni karakteristične jednadžbe p1, p2,…, pn biti isti za sve varijabilne funkcije(struje i naponi).
Karakteristična jednačina može se konstruirati korištenjem različitih metoda. Prva metoda je klasična, kada se karakteristična jednadžba sastavlja striktno u skladu s diferencijalnom jednadžbom prema klasičnoj shemi. Prilikom izračunavanja prolaznih procesa u složena šema sistem “m” diferencijalnih jednadžbi se sastavlja prema Kirchhoffovim zakonima za dijagram kola nakon prebacivanja. Kako su korijeni karakteristične jednadžbe zajednički za sve varijable, rješenje sistema diferencijalnih jednadžbi se izvodi u odnosu na bilo koju varijablu (opciono). Kao rezultat rješenja dobiva se nehomogena diferencijalna jednadžba s jednom varijablom. Sastaviti karakterističnu jednačinu u skladu s rezultirajućom diferencijalnom jednadžbom i odrediti njene korijene.
Primjer. Sastavite karakterističnu jednačinu i odredite njene korijene za varijable na dijagramu na sl. 59.1. Parametri elemenata su specificirani u opštem obliku.
Sistem diferencijalnih jednadžbi prema Kirchhoffovim zakonima:
Hajde da riješimo sistem jednadžbi za varijablu i3, kao rezultat dobijemo nehomogenu diferencijalnu jednačinu:
Drugi način da se sastavi karakteristična jednačina je da se izjednači sa nulom glavna determinanta Kirchhoffovog sistema jednačina za varijable slobodne komponente.
Neka slobodna komponenta proizvoljne struje ima oblik iksv = Akept, tada:
Sistem jednačina za slobodne komponente dobija se iz Kirchhoffovog sistema diferencijalnih jednačina zamjenom izvoda varijabli faktorom p, a integrala 1/p. Za primjer koji se razmatra, sistem jednadžbi za slobodne komponente ima oblik:
Karakteristična jednadžba i njen korijen:
Treći način za sastavljanje karakteristične jednačine (inženjering) je izjednačavanje ulaznog operatorskog otpora kola na nulu u odnosu na bilo koju njegovu granu.
Otpor operatora elementa se dobija iz njegovog kompleksnog otpora jednostavnom zamjenom faktora jω sa p, dakle
Za dotični primjer:
Treća metoda je najjednostavnija i najekonomičnija, stoga se najčešće koristi pri proračunu prolaznih procesa u električnim krugovima.
Korijeni karakteristične jednadžbe karakteriziraju slobodni prolazni proces u kolu bez izvora energije. Ovaj proces se odvija uz gubitke energije i zbog toga propada tokom vremena.
U opštem slučaju, red diferencijalne jednadžbe koja opisuje prelazni proces u kolu, a samim tim i stepen karakteristične jednadžbe i broj njenih korena jednaki su broju nezavisnih početni uslovi, odnosno broj nezavisnih uređaja za skladištenje energije (kalemovi L i kondenzatori C).
Ako shema strujnog kola sadrži paralelno spojene kondenzatore C1, C2,... ili serijski spojene zavojnice L1, L2,..., tada se pri proračunu prelaznih procesa moraju zamijeniti jednim ekvivalentnim elementom SE = C1 + C2+... ili LE = L1 + L2+... dakle, opšti pogled
rješenja za bilo koju varijablu pri proračunu prelaznog procesa mogu se kompajlirati samo iz analize dijagrama kola, bez sastavljanja i rješavanja sistema diferencijalnih jednačina.
) Za primjer o kojem smo gore govorili. = ||A||a ik n
1 oduzimanjem vrijednosti λ od dijagonalnih elemenata. Ova determinanta je polinom u odnosu na X - karakterističan polinom. Kada se otvori, X. u. je napisano ovako: Gdje = S 1 + a 11 +... a 22 ann - tzv matrični trag, S 2 a ik- zbir svih glavnih minora 2. reda, tj. minora oblika i k), itd., i S Za primjer o kojem smo gore govorili.- matrična determinanta a ik. Korijeni H. u. λ 1 , λ 2 ,..., λ Za primjer o kojem smo gore govorili. nazivaju se svojstvene vrijednosti matrice . Za realnu simetričnu matricu, kao i za hermitsku matricu, svi λ k . Za realnu simetričnu matricu, kao i za hermitsku matricu, svi λ su realne, realna koso-simetrična matrica ima sve λ . Za realnu simetričnu matricu, kao i za hermitsku matricu, svi λ| = 1.
čisto imaginarni brojevi; u slučaju realne ortogonalne matrice, kao i unitarne matrice, sve |λ
H.u. nalazi se u raznim oblastima matematike, mehanike, fizike i tehnologije. U astronomiji, kada se određuju sekularne perturbacije planeta, dolaze i do hemijskih jednačina; otuda drugo ime za X. u. - prastara jednačina.
2) H. u. linearna diferencijalna jednadžba sa konstantnim koeficijentimaλ a 0 (y) + n (a 1 g) +... + n-1 + a n-1 y" = 0
a n y Algebarska jednadžba koja se dobiva iz date diferencijalne jednadžbe nakon promjene funkcije at
2) H. u. linearna diferencijalna jednadžba sa konstantnim koeficijentimaλ a ik + i njegove derivacije po odgovarajućim potencijama λ, tj. jednačinaλ a 1 + ... + n-1 a n-1 + a n-1 y" = 0.
y" Algebarska jednadžba koja se dobiva iz date diferencijalne jednadžbe nakon promjene funkcije = Do ove jednačine se dolazi pronalaženjem određenog rješenja oblika λ se X
za datu diferencijalnu jednačinu. Za sistem linearnih diferencijalnih jednadžbi
H.u. napisano pomoću determinante H.u. matrice =
A Veliki Sovjetska enciklopedija. 1969-1978 .
. - M.: Sovjetska enciklopedija
Pogledajte šta je "Karakteristična jednačina" u drugim rječnicima: U mnogim slučajevima, koji se javljaju u sistemima, opisani su sistemom običnih linearnih diferencijalnih jednadžbi sa konstantnim koeficijentima, koji se u prilično opštem slučaju mogu svesti na diferencijalnu jednačinu... Enciklopedija tehnologije
Algebarska jednadžba oblika: Determinanta u ovoj formuli se dobija iz determinante matrice oduzimanjem vrijednosti x od dijagonalnih elemenata; predstavlja polinom u x i naziva se karakteristični polinom... Veliki enciklopedijski rječnik
karakteristična jednačina- - [V.A. Englesko-ruski rječnik relejne zaštite] Teme relejne zaštite EN karakteristična jednačina ... Vodič za tehnički prevodilac
Algebarska jednadžba oblika. Determinanta u ovoj formuli se dobija iz determinante matrice x dijagonalnih elemenata; to je polinom po x i naziva se karakteristični polinom. * * * KARAKTERISTIKE… … Encyclopedic Dictionary
karakteristična jednačina- būdingoji lygtis statusas T sritis automatika atitikmenys: engl. karakteristična jednačina; jednačina performansi vok. charakteristische Gleichung, f; Stammgleichung, f rus. karakteristična jednadžba, n pranc. équation caractéristique, f … Automatikos terminų žodynas
karakteristična jednačina- būdingoji lygtis statusas T sritis fizika atitikmenys: engl. karakteristična jednačina; jednačina performansi vok. Charakteristische Gleichung, f rus. karakteristična jednadžba, n pranc. équation caractéristique, f … Fizikos terminų žodynas
karakteristična jednačina Enciklopedija "Vazduhoplovstvo"
karakteristična jednačina- karakteristična jednačina. U mnogim slučajevima, fizički procesi koji se dešavaju u sistemima opisuju se sistemom običnih linearnih diferencijalnih jednadžbi sa konstantnim koeficijentima, koji se u prilično opštem slučaju mogu smanjiti... Enciklopedija "Vazduhoplovstvo"
Sekularna jednadžba, vidi čl. Karakteristični polinom... Mathematical Encyclopedia
Karakteristični polinom je polinom koji određuje svojstvene vrijednosti matrice. Drugo značenje: Karakteristični polinom linearnog rekurenta je polinom. Sadržaj 1 Definicija ... Wikipedia
Knjige
- Karakteristični Liejevi prstenovi i nelinearne integrabilne jednačine, Zhiber A.V.. Knjiga je posvećena sistematskom prikazu algebarskog pristupa proučavanju nelinearnih integrabilnih parcijalnih diferencijalnih jednačina i njihovih diskretnih analoga, zasnovanih na konceptu...
Karakteristična jednačina ima oblik:
Za određivanje vrste slobodne komponente potrebno je sastaviti i riješiti karakterističnu jednačinu: z(p) = 0. Za pisanje karakteristične jednačine potrebno je nacrtati dijagram u kojem treba zamijeniti sve izvore emf i struje. svojim unutrašnjim otpora i otpora uzeti induktivnost i kapacitivnost respektivno jednake Pl i , tada je potrebno prekinuti bilo koju granu ovog kola, zapisati njegov početni otpor u odnosu na tačke prekida, izjednačiti ga sa nulom, riješiti i odrediti korijene p, ako su korijeni ispostavi da je realno negativan, tada je slobodna komponenta željene funkcije:
, gdje je m broj korijena jednadžbe;
Roots; - trajno integrisan.
Ako se pokaže da su korijeni jednadžbe karaktera kompleksno konjugirani, tada će slobodno stanje imati oblik:
gdje je frekvencija slobodnih vibracija;
Početna faza slobodnih oscilacija.
8.Transition time. Određivanje praktično t pp. Proračun vremena procesa tranzicije.
Vrijeme prijelaznog procesa ovisi o koeficijentu slabljenja. Inverzna vrijednost se naziva vremenska konstanta i iznosi vrijeme, tokom pri čemu će se vrijednost slobodne komponente prolaznog procesa smanjiti za e=2,72 puta. Vrijednost ovisi o krugu i parametrima serijska veza r i L = , i u serijskoj vezi
95% završetak procesa tranzicije 3.
Najlakši način da se konstruišu krive slobodnih komponenti prolaznog procesa je postavljanje vrijednosti vremena t na 0, ,2.....Ako postoji nekoliko realnih korijena, onda se rezultujuća kriva dobija zbrajanjem ordinate pojedinačnih pojmova (slika 1.)
Slika 1:
9.10, Prolazni proces u r, C – krugovima kada su spojeni na izvor DC napon. Izvršiti analizu klasičnom metodom; dati analitičke izraze za U C (t); iC(t); grafika. (Klasična metoda).
Jednadžba stanja rC kola nakon prebacivanja je sljedeća:
(1) ili rC (2)
Njegovo rešenje: 
Kapacitet C nakon zatvaranja ključa na t će biti napunjen do stabilne vrijednosti
Pošto su početni uslovi jednaki nuli, prema komutacionom zakonu 
pri t=0, ili 0=A, odakle je A=-E.
Rješenje jednačine (2) će poprimiti oblik:
Struja kola i(t)=C
Slika 1.
Slika 2.
Grafikoni promjena napona i struje i(t) prikazani su na slikama 1 i 2. Iz slika se vidi da napon na kondenzatoru eksponencijalno raste od 0 do E, dok jačina struje u trenutku uključivanja naglo dostiže vrijednost E/r, a zatim se smanjuje na nulu.
11.12.Prolazni proces u r, C – kolima kada je priključen na sinusni izvor napona. Izvršiti analizu klasičnom metodom; dati analitičke izraze za U C (t); iC(t); grafika. (Klasična metoda).
Jednačina stanja rC kola u prelaznom režimu je sljedeća
rC 
.
Rješenje ove jednačine:
Besplatna komponenta
gdje je =rC
Budući da je kolo linearno, tada će se sa sinusnim efektom i u stacionarnom stanju napon na kondenzatoru također mijenjati po sinusnom zakonu s frekvencijom ulaznog efekta. Stoga ćemo za određivanje = koristiti metodu kompleksnih amplituda :
; 
Uzimajući u obzir da je j= , dobijamo:
Konstanta integracije A slobodne komponente
Nađimo iz početnih uslova u kolu uzimajući u obzir komutacijski zakon:
.Na t=0 posljednji izraz ima oblik
Gdje je A=-
Zbrajanjem komponenti i dobijamo konačni izraz za napon na kondenzatoru u prolaznom modu:
= + = 
- (1)
Analiza izraza (1) pokazuje da prelazni proces u rC kolu pod sinusoidnim uticajem zavisi od početne faze emf izvora u trenutku uključivanja i od vremenske konstante rC kola.
Ako je , tada je =0 i stabilno stanje će se pojaviti u kolu odmah nakon prebacivanja, tj.
Kada je napon = - , tj. Napon na kondenzatoru odmah nakon prebacivanja može dostići gotovo dvostruku vrijednost pozitivnog predznaka, a zatim se postepeno približava =.
Fazna razlika će dovesti jednačinu (1) do oblika:
Razlika između ovog načina rada i prethodnog je u tome što napon na kondenzatoru odmah nakon prebacivanja može dostići gotovo dvostruko veću negativnu vrijednost.
Za razmatrano Rc kolo sa sinusoidnim izvorom struje u stacionarnom stanju, početna faza ulazni napon ne igra nikakvu ulogu, ali u procesu tranzicije njegov uticaj je značajan.
13.Prolazni proces u r, L, C – krugovima kada je priključen na izvor konstantnog napona. Batch proces. Analitički izrazi za i(t), grafika. (Klasična metoda).
Korijeni su stvarni, negativni, različiti.
I(t)=I usta +A1e p 1 t +A2e p 2 t
Proces je periodičan:
t=0 (i(0)=A1+A2; A1=-A2
{ 
t=0 i l (0)*r+L +Uc(0)=E A1=-A2= ()
i l (t)= ( 
)
14.Prolazni proces u r, L, C – krugovima kada je priključen na izvor konstantnog napona. Kritični proces. Analitički izrazi za i(t), grafika. (Klasična metoda).
i l (t)=i usta +(B1+B2*t)*
t=0: i l (0)=β1=0
Ako se ispostavi da su korijeni stvarni, negativni, jednaki, tada je proces kritičan.
15.Prolazni proces u r, L, C – krugovima kada je priključen na izvor konstantnog napona. Oscilatorni proces. Analitički izraz za i(t), grafika. (Klasična metoda).
P t = -δ±j*ω St ω St =
Korijeni su negativni realni, neki složeni konjugati.
i l (t)=i usta A1e - δt *sin(ω St t+ψ)
i l (t)=i usta +(M*cos ω svjetlo t+N*sin ω svjetlo t)*
i l (t)= * 
= *
16. Prolazni proces u r, L, C – kolima kada su spojeni na sinusni izvor napona. Aperiodični proces. Analitički izraz za i(t), grafika. (Klasična metoda).
R(t)=E max *sin(ωt+ψ)
2. 
U klasičnom broju jednadžbi u ovom slučaju jednak je broju grana kola
Metoda pronalazi rješenje u obliku zbira opšteg i posebnog rješenja. Proračun prolaznog procesa opisan je sistemom običnih diferencijalnih jednadžbi sastavljenih jednom od metoda proračuna za trenutne vrijednosti vremenskih funkcija. Rješenje za svaku varijablu ovog sistema nalazi se u obliku zbira opštih i partikularnih rješenja. Za sastavljanje jednačine može se koristiti: metoda zasnovana na primjeni Kirchhoffovih zakona, metoda čvornih potencijala, metoda struja petlje itd. Na primjer, sistem diferencijalnih jednadžbi sastavljen nakon komutacije prema Kirchhoffovom prvom i drugom zakonu ima oblik:
na primjer,
Broj jednačina u ovom slučaju jednak je broju grana kola. Neka je potrebno pronaći struju i k u grani sa brojem K. Eliminirajući struje grana u nizu, kao rezultat dobijamo struju i k i njene derivate do reda n:
Redoslijed diferencijalne jednadžbe n određen je brojem nezavisnih reaktivnih elemenata kola (m). Obično n=m, ali ovisno o načinu povezivanja može biti i n Serijski spojeni kapacitivni elementi mogu se zamijeniti jednim elementom, kao što se paralelno povezani induktivni elementi mogu zamijeniti jednim ekvivalentnim. Na slici 9.5 prikazana je zamjena 2 kondenzatora spojena u seriju sa jednim ekvivalentnim. Općenito, red diferencijalne jednadžbe n je jednak: n=n lc -n ce -n lj, gdje je n lc broj reaktivnih elemenata (L i C) u kolu, n ce je broj kapacitivnih kola, n lj je broj induktivnih čvorova ili sekcija. Pod kapacitivnim se podrazumijeva kolo koje se sastoji od kapacitivnih elemenata ili kapacitivnih elemenata i idealnih emf izvora, slika 9.6.a Pod induktivnim se podrazumijeva čvor u koji se konvergiraju induktivne grane ili induktivni ogranci i izvori struje (slika 9.6.b). sekcije koje prelaze samo induktivne grane ili induktivne grane i izvori struje. Imajte na umu da faza sastavljanja diferencijalne jednadžbe nije obavezna i da se struja ili napon prijelaza može pronaći bez sastavljanja jednadžbe. Kao što je naznačeno, u klasičnoj metodi proračuna prelaznih procesa rješavaju se jednačine Konkretno rješenje opisuje režim koji se naziva prisilni. Rješenje homogene jednadžbe (desna strana je nula) opisuje proces u odsustvu vanjskih EMF i izvora struje i naziva se slobodnim. Slobodne i prisilne struje, naponi i naboji se smatraju u skladu s tim. Dakle, struja u grani sa brojem K je predstavljena kao zbir. Definicija. Karakteristična jednačina linearnog operatora f je jednačina oblika , gdje je λ bilo koji realan broj, A je matrica linearnog operatora, E je matrica identiteta istog reda. Polinom
pozvao karakteristični polinom matrica A (linearni operator f). U matričnom obliku, karakteristična jednadžba ima sljedeći oblik: Prema tome, izjednačavanjem karakterističnog polinoma sa nulom, dobijamo jednačinu stepena y, gdje je λ nepoznata, dobijamo vrijednosti njegovih korijena - karakteristične brojeve ove matrice. Karakteristični korijeni igraju važnu ulogu u mnogim područjima matematike. Razmotrimo jednu od primjena karakterističnih korijena - vrlo važnog alata u proučavanju linearnih prostora, kao i u rješavanju mnogih primijenjenih problema linearne algebre. Skup svih korijena karakteristične jednadžbe naziva se spektar operatora f(svaki korijen se razmatra sa višestrukim brojem koji ima u karakterističnoj jednadžbi). Primjer. Pronađite karakteristične korijene matrice. Kreirajmo matricu Izjednačavajući karakteristični polinom sa nulom, dobijamo kvadratnu jednačinu Tada su korijeni jednadžbe jednaki Definicija. Neka je f linearni operator prostora i neka je neki vektor različit od nule za koji je jednakost gdje je pravi broj. Tada se vektor naziva svojstveni vektor operatora i matrica njegovog operatora, svojstvena vrijednost ili svojstvena vrijednost transformacije. U ovom slučaju se kaže da se svojstveni vektor odnosi na svojstvenu vrijednost. Svojstveni vektori igraju važnu ulogu kako u samoj matematici tako iu njenoj primjeni. Na primjer, rezonancija, u kojoj se prirodne frekvencije vibracija sistema poklapaju sa frekvencijom vibracija vanjskih sila. U matematici, sopstveni vektori su korisni u rešavanju sistema diferencijalnih jednačina. Teorema. Ako linearni operator f ima matricu A u svojoj bazi (prva baza) i matricu B u svojoj bazi (druga baza), onda vrijedi jednakost: . Posljedično, kada se prijeđe na novu bazu, karakterističan polinom linearnog operatora se ne mijenja. ◌ Ako je T matrica prijelaza s prve baze na drugu, onda . Zatim transformiramo desnu stranu jednakosti ●
Teorema. Da bi broj λ 0 iz polja P bio sopstvena vrijednost vektora prostora L n nad P, potrebno je i dovoljno da broj λ 0 bude karakteristični korijen operatora f. Doc. I. Nužnost. Neka λ 0
vlastita vrijednost operatora f, zatim unutra Ln postoji svojstveni vektor takav da . Neka S druge strane, jer , gdje je matrica linearnog operatora u datoj bazi, onda Izjednačavajući desne strane (1) i (2) dobijamo: Jednačine (3) znače da je numerički vektor sa koordinatama Vektor je različit od nule (pošto je svoj), stoga sistem (4) ima rješenje različito od nule, pa mu je determinanta 0. i stoga je transpozibilna determinanta jednaka 0. Ako shema strujnog kola sadrži paralelno spojene kondenzatore C1, C2,... ili serijski spojene zavojnice L1, L2,..., tada se pri proračunu prelaznih procesa moraju zamijeniti jednim ekvivalentnim elementom SE = C1 + C2+... ili LE = L1 + L2+... λ 0
– korijen karakteristične jednačine. II. Adekvatnost. Neka λ 0
– karakteristični korijen operatora u nekoj bazi Zaista, ako λ 0
je karakteristični korijen, tada će biti zadovoljena jednakost (6), a samim tim i jednakost (5), a to će značiti da sistem (4) ima rješenja različita od nule. Odaberimo neko rešenje sistema (4) različito od nule: numerički vektor Razmotrimo vektor i za njega će biti zadovoljena jednakost (2) i, na osnovu formule, vrijedi jednakost (1), gdje je matrica operatora u bazi IN. To implicira jednakost, što znači da je vektor svojstveni vektor operatora kojem odgovara svojstvena vrijednost λ 0
. To je bilo ono što je trebalo dokazati. Teorema je dokazana. Komentar. Da bi se pronašle vlastite vrijednosti operatora, potrebno je sastaviti i riješiti jednačinu (5). Da biste pronašli svojstvene vektore operatora, potrebno je kreirati sistem jednačina (4) i pronaći osnovni skup rješenja za ovaj sistem. Za kontrolu ispravnosti izračunavanja svojstvenih vrijednosti (mogu biti podudarne ili složene) koriste se dvije činjenice: 1) 2) Primjer. Pronađite svojstvene vrijednosti i svojstvene vektore 3) . , Neka je slobodna varijabla, tada ćemo dobiti vektor Vježbajte. Provjerite vektor.
je predstavljen kao zbir opštih i partikularnih rešenja.
ili
.
.
je onda njegova koordinatna linija u nekoj bazi
(3)
je rješenje sljedećeg sistema jednačina (4).
(4)
(5)
(6)
. Dokažimo to λ 0
je sopstvena vrijednost operatora A.
. Tada su jednakosti (3) zadovoljene.
, gdje je posljednji zbir matrice tragova zbir dijagonalnih elemenata.
.
.
Izjednačavanjem sa nulom dobijamo . .
.
.
.